Revision NotesExam QuestionsPast Papers
A LevelPhysicsCIERevision Notes4. Forces, Density & Pressure4.2 Equilibrium of ForcesPrinciple of Moments

Syllabus Edition

First teaching 2023

First exams 2025

|

Principle of Moments (CIE A Level Physics)

Revision Note

Leander

Author

Leander

Last updated

The principle of moments

  • The principle of moments states:

For a system to be in equilibrium, the sum of clockwise moments about a point must be equal to the sum of the anticlockwise moments (about the same point)

Moments acting on a balanced beam

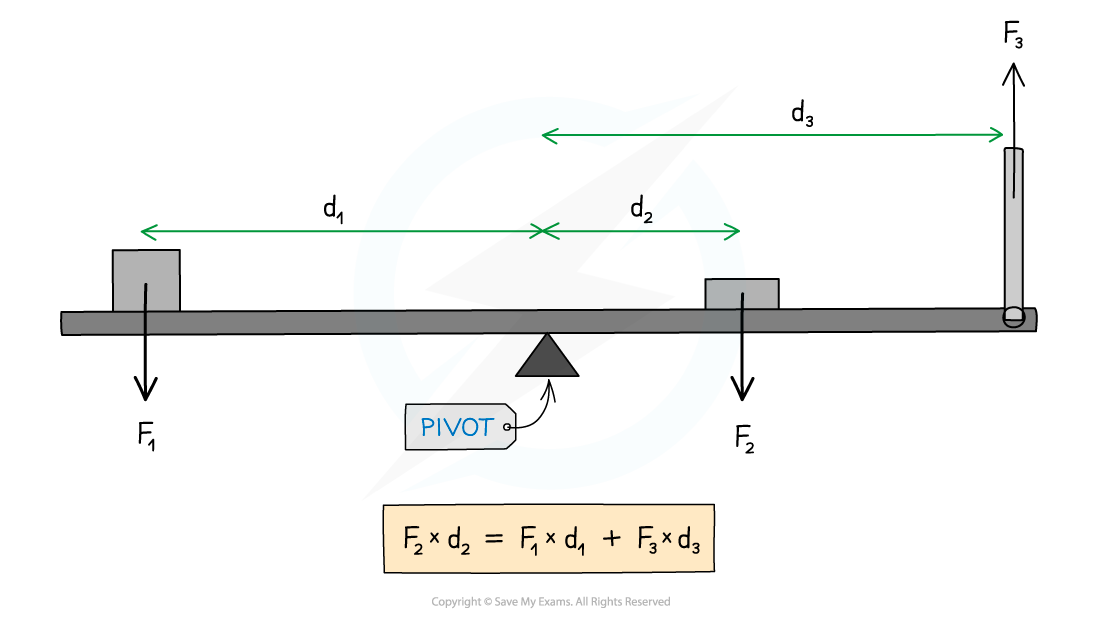
Principle of moments, downloadable AS & A Level Physics revision notes

The sum of the anticlockwise moments of forces F1 and F3 are equal to the clockwise moment of force F2

  • In the above diagram:
    • Force F2 is supplying a clockwise moment;
    • Forces F1 and F3 are supplying anticlockwise moments
    • The clockwise and anticlockwise moments are equal because the beam is in equilibrium

F subscript 2 d subscript 2 space equals space open parentheses F subscript 1 d subscript 1 close parentheses space plus space open parentheses F subscript 3 d subscript 3 close parentheses

Worked example

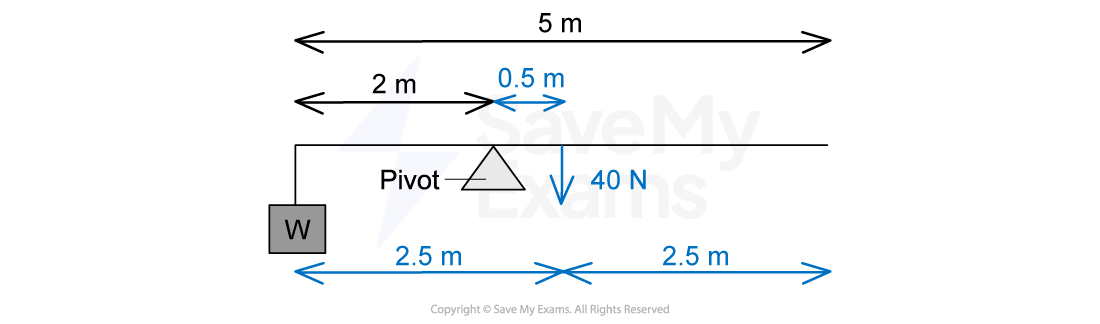
A uniform beam of weight 40 N is 5 m long and is supported by a pivot situated 2 m from one end.

When a load of weight W is hung from that end, the beam is in equilibrium as shown in the diagram.

WE - principle of moments question image, downloadable AS & A Level Physics revision notes

What is the value of W?

A     10 N               B     50 N               C     25 N               D     30 N

Answer:

Step 1: List the known quantities

  • Weight acting on beam, WB = 40 N
  • Weight acting on mass = W
  • Length of beam = 5 m
  • Distance to pivot (from end of beam), dW = 2 m

Step 2: Recall the principle of moments

clockwise moments = anticlockwise moments

Step 3: Calculate the clockwise moment

  • Because the beam is uniform, the force of weight acting upon it will be exerted from its centre of gravity
  • This will be the middle of the beam

Centre space of space gravity space equals space 5 over 2 space equals space 2.5 space straight m (from the end of the beam)

  • The pivot is 2 m from the end of the beam
  • Therefore, the force acts at a distance of 2.5 − 2 = 0.5 m from the pivot

4-2-1-we-principle-of-moments-answer-cie-new

clockwise space moment space equals space W subscript B d

clockwise space moment space equals space 40 space cross times space 0.5

clockwise space moment space equals space 20 space straight N space straight m

Step 4: Calculate the anticlockwise moment

anticlockwise space moment space equals space W d subscript W

anticlockwise space moment space equals space W space cross times space 2 space equals space 2 W

Step 5: Equate the clockwise and anticlockwise moments to calculate

clockwise space moment space equals space anticlockwise space moment

20 space equals space 2 W

W space equals space 20 over 2 space equals space 10 space straight N

  • Therefore, the answer is A

Examiner Tip

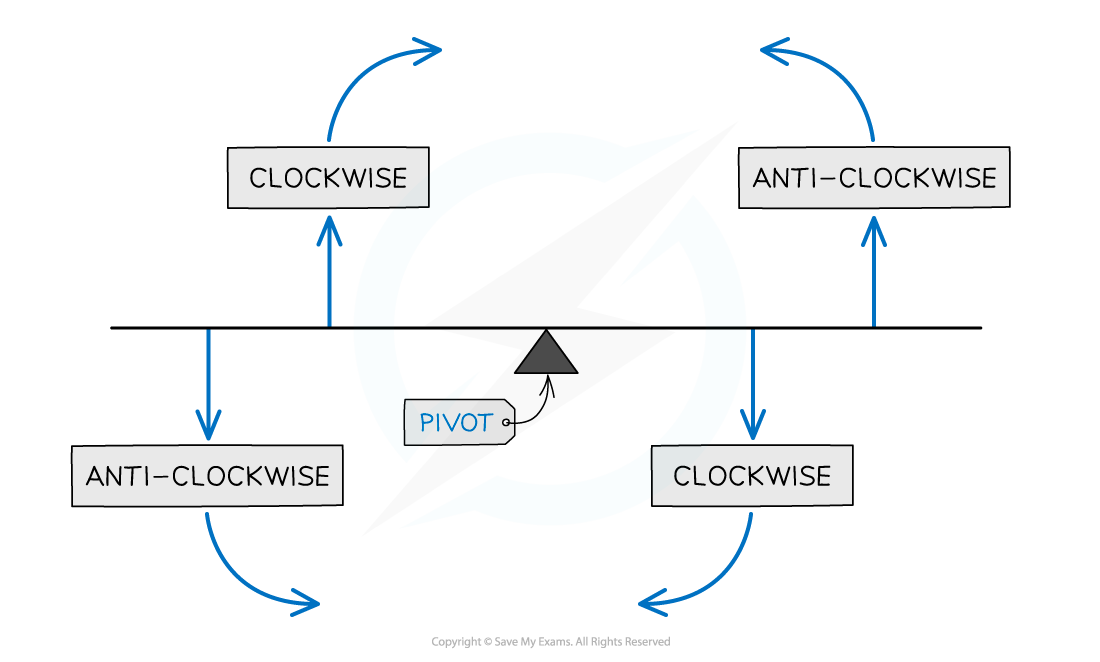
Make sure that all the distances are in the same units and you’re considering the correct forces as clockwise or anticlockwise, as seen in the diagram belowClockwise or anticlockwise moment, downloadable AS & A Level Physics revision notes

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Turning Effects of ForcesNext:Conditions for Equilibrium
    Leander

    Author: Leander

    Expertise: Physics

    Leander graduated with First-class honours in Science and Education from Sheffield Hallam University. She won the prestigious Lord Robert Winston Solomon Lipson Prize in recognition of her dedication to science and teaching excellence. After teaching and tutoring both science and maths students, Leander now brings this passion for helping young people reach their potential to her work at SME.