Revision NotesExam QuestionsPast Papers
A LevelPhysicsCambridge (CIE)Revision Notes3. DynamicsLinear Momentum & its ConservationConservation of Momentum

Syllabus Edition

First teaching 2023

First exams 2025

|

Conservation of Momentum (Cambridge (CIE) A Level Physics)

Revision Note

Leander Oates

Written by: Leander Oates

Reviewed by: Caroline Carroll

Updated on

The principle of conservation of momentum

  • The principle of conservation of linear momentum states that:

    The total linear momentum before a collision is equal to the total linear momentum after a collision unless the system is acted on by a resultant external force

  • Therefore:

momentum before = momentum after

  • Momentum is a vector quantity, therefore:

    • opposing vectors can cancel each other out, resulting in a net momentum of zero

    • an object that collides with another object and rebounds, has a positive velocity before the collision and a negative velocity after 

  • Momentum is always conserved

  • For example:

    • Ball A moves with an initial velocity of u subscript A

    • Ball A collides with Ball B which is stationary

  • After the collision, both balls travel in opposite directions

    • Taking the direction of the initial motion of Ball A as the positive direction (to the right) 

    • The momentum before the collision is

      p subscript b e f o r e end subscript space equals space m subscript A u subscript A space plus space 0

    • The momentum after the collision is

      p subscript a f t e r end subscript space equals space minus m subscript A v subscript A space plus thin space m subscript B v subscript B

  • The minus sign shows that Ball A travels in the opposite direction to the initial travel 

    • If an object is stationary, like Ball B before the collision, then it has a momentum of zero

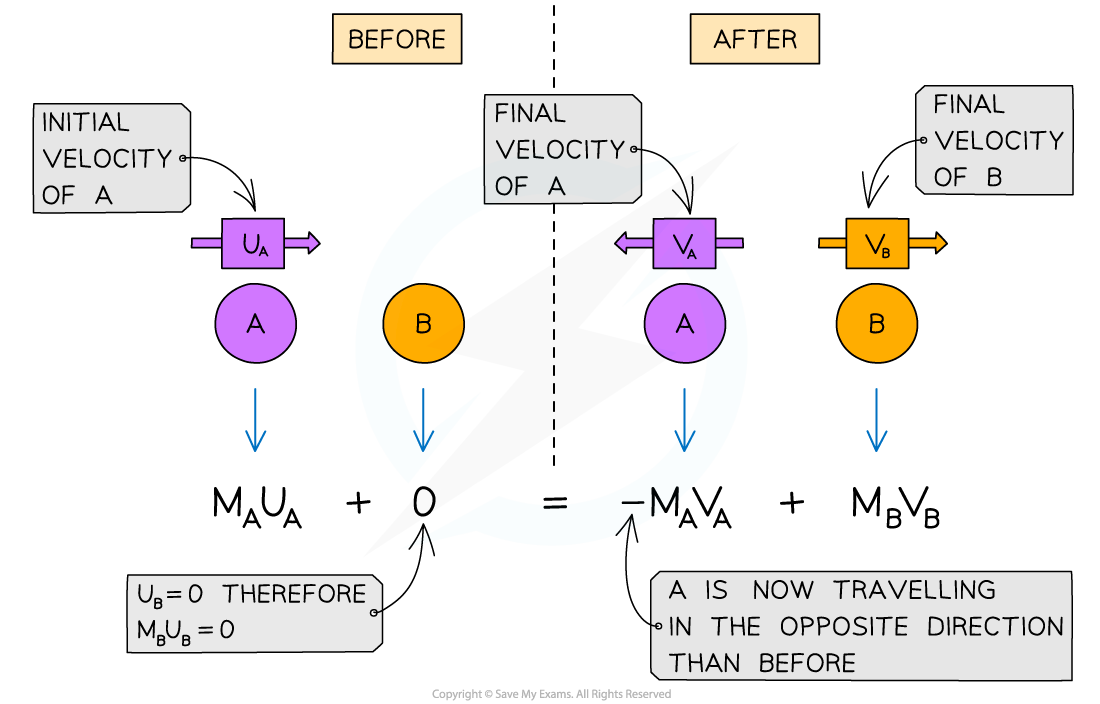
conversation-of-momentum

The conservation of momentum for two objects A and B colliding then moving apart

External and internal forces

  • External forces are forces that act on a structure from outside e.g. friction and weight

  • Internal forces are forces exchanged by the particles in the system e.g. tension in a string

    • Which forces are internal or external will depend on the system itself

  • A system with no external forces acting can be described as a closed or isolated system

Internal and external forces for a mass on a spring

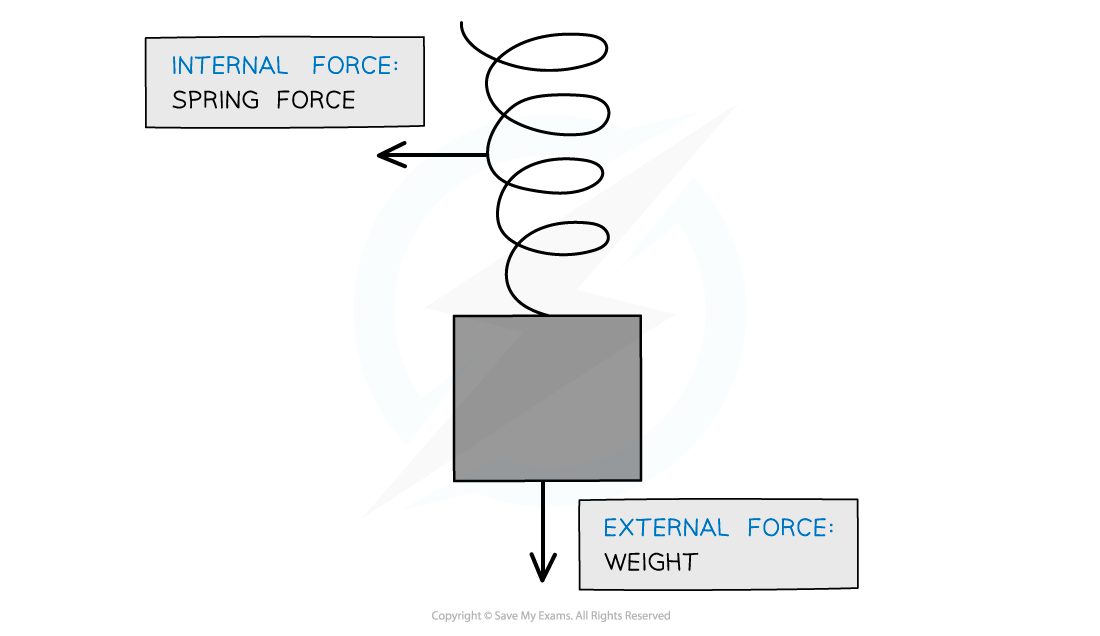
External and internal forces on a mass on a spring, downloadable AS & A Level Physics revision notes

The spring force is internal to the system because the spring is part of the system, whereas weight (the gravitational pull of the Earth on the mass) is external to the system

Collisions in one & two dimensions

One-dimensional momentum problems

  • Recall that linear momentum is p = mv

  • Using the conversation of linear momentum, it is possible to calculate missing velocities and masses of components in a system

  • Elastic collisions are commonly those where objects colliding do not stick together and then move in opposite directions

  • Inelastic collisions are where objects collide and stick together after the collision

  • To find out whether a collision is elastic or inelastic, compare the amount of kinetic energy in the system before and after the collision

    • If the kinetic energy is conserved, it is an elastic collision

    • If the kinetic energy is not conserved, it is an inelastic collision

Worked Example

Trolley A, of mass 0.80 kg.

Trolley A collides head-on with stationary Trolley B at a velocity of 3.0 m s-1.

Trolley B has twice the mass of Trolley A. The trolleys stick together.

(a) Using the conservation of momentum, calculate the common velocity of both trolleys after the collision.

(b) Prove that the collision is inelastic.

Answer:

(a)

Step 1: List the known quantities

  • Mass of Trolley A, mA = 0.80 kg

  • Velocity of Trolley A, vA = 3.0 m s-1

  • Mass of Trolley B, mB = 2mA = 1.60 kg

Step 2: Determine the momentum before the collision

p subscript b e f o r e end subscript space equals space m subscript A v subscript A space plus space m subscript B v subscript B

p subscript b e f o r e end subscript space equals space open parentheses 0.80 space cross times space 3.0 close parentheses space plus space 0

p subscript b e f o r e end subscript space equals space 2.4 space kg space straight m space straight s to the power of negative 1 end exponent

  • Since Trolly B was stationary before the collision, its momentum is zero

Step 3: Determine the momentum after the collision

p subscript a f t e r end subscript space equals space open parentheses m subscript A space plus space m subscript B close parentheses space cross times space v subscript A plus B end subscript

p subscript a f t e r end subscript space equals space open parentheses 0.80 space plus space 1.60 close parentheses space cross times space v subscript A plus B end subscript

p subscript a f t e r end subscript space equals space 2.4 space cross times space v subscript A plus B end subscript

Step 4: Equate the momentum before and after the collision using the principle of conservation of momentum

momentum before collision = momentum after collision

p subscript b e f o r e end subscript space equals space p subscript a f t e r end subscript

2.4 space equals space 2.4 space cross times space v subscript A plus B end subscript

Step 5: Calculate the common velocity of both trolleys after the collision

v subscript A plus B end subscript space equals space fraction numerator 2.4 over denominator 2.4 end fraction

v subscript A plus B end subscript space equals space 1.0 space straight m space straight s to the power of negative 1 end exponent

(b)

Step 1: Calculate the kinetic energy of the system before the collision

E subscript k space b e f o r e end subscript space equals space 1 half m subscript A open parentheses v subscript A close parentheses squared space plus space 1 half m subscript B open parentheses v subscript B close parentheses squared

E subscript k space b e f o r e end subscript space equals space 0.5 space cross times space 0.80 space cross times space open parentheses 3.0 close parentheses squared space plus space 0

E subscript k space b e f o r e end subscript space equals space 3.6 space straight J

  • Since trolly B was stationary before the collision, its kinetic energy is zero

Step 2: Calculate the kinetic energy of the system after the collision

E subscript k space a f t e r end subscript space equals space 1 half m subscript A plus B end subscript open parentheses v subscript A plus B end subscript close parentheses squared

E subscript k space a f t e r end subscript space equals space 0.5 space cross times space open parentheses 0.8 space plus space 1.6 close parentheses space cross times space open parentheses 1.0 close parentheses squared

E subscript k space a f t e r end subscript space equals space 1.2 space straight J

Step 3: State whether the collision was inelastic

  • The kinetic energy before the collision, 3.6 J, was greater than the kinetic energy after the collision, 1.2 J

  • Therefore, the kinetic energy of the system is not conserved, and the collision is inelastic

Examiner Tips and Tricks

If an object is stationary or at rest, its velocity equals 0, therefore, the momentum and kinetic energy are also equal to 0.

When an inelastic collision occurs in which two objects are stuck together, treat the final object as a single object with a mass equal to the sum of the two individual objects.

Two-dimensional momentum problems

  • Since momentum is a vector, in two dimensions it can be split up into its x and y components

  • See Scalars & Vectors for a reminder on resolving vectors

Worked Example

A ball is thrown at a vertical wall.

The ball is thrown from position S with an initial velocity of 15.0 m s-1 at 60.0° to the horizontal.

The ball hits the wall at position P and rebounds at a velocity of 4.6 m s-1

The mass of the ball is 60 × 10-3 kg.

Calculate the change in momentum of the ball as it bounces off the wall.

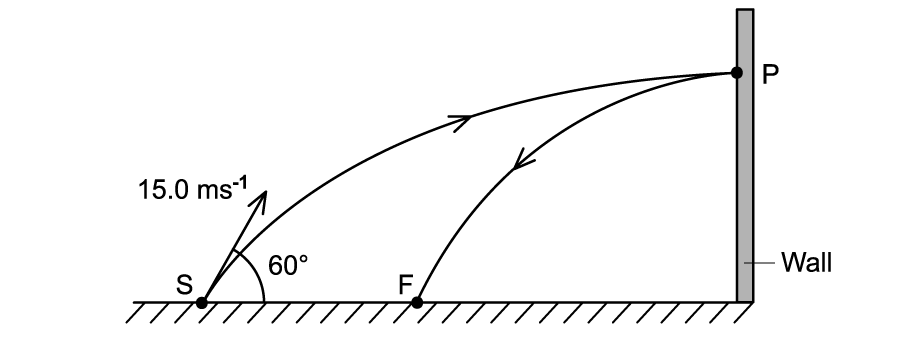
Answer:

Step 1: List the known quantities and assign direction

  • Initial horizontal velocity, vi = 15.0 m s-1 at 60.0° to the horizontal

  • Final horizontal velocity, vf = −4.6 m s-1

  • Mass of ball, m = 60 × 10-3 kg

Step 2: State the change in momentum equation

increment p space equals space m open parentheses v subscript f space minus space v subscript i close parentheses

Step 3: Calculate the initial velocity

  • A change in momentum is only due to the horizontal velocity component for projectile motion

v subscript i space equals space 15.0 space cross times space cos open parentheses 60 close parentheses

v subscript i space equals space 7.5 space straight m space straight s to the power of negative 1 end exponent

Step 4: Calculate the change in momentum

increment p space equals space m open parentheses v subscript f space minus space v subscript i close parentheses

increment p space equals space open parentheses 60 cross times 10 to the power of negative 3 end exponent close parentheses space cross times space open parentheses negative 4.6 space minus space 7.5 close parentheses

increment p space equals space minus 0.73 space straight N space straight s

  • The answer should be negative because the ball is traveling in the opposite direction after it rebounds

Examiner Tips and Tricks

 For problems in two dimensions, make sure you’re confident resolving vectors.

Here is a little trick to help you remember which component is cosine or sine of the angle for a vector R:

Vector components, downloadable AS & A Level Physics revision notes

Resolving vectors with sine and cosine

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Terminal VelocityNext:Elastic & Inelastic Collisions
    Author
    Reviewer
    Leander Oates

    Author: Leander Oates

    Expertise: Physics

    Leander graduated with First-class honours in Science and Education from Sheffield Hallam University. She won the prestigious Lord Robert Winston Solomon Lipson Prize in recognition of her dedication to science and teaching excellence. After teaching and tutoring both science and maths students, Leander now brings this passion for helping young people reach their potential to her work at SME.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.