A LevelPhysicsCambridge (CIE)Revision Notes3. DynamicsMomentum & Newton’s Laws of MotionForce & Momentum

Force & Momentum (Cambridge (CIE) A Level Physics): Revision Note

Exam code: 9702

Leander Oates

Written by: Leander Oates

Reviewed by: Caroline Carroll

Updated on

Force & momentum

  • Force is defined as the rate of change of momentum 

F space equals space fraction numerator increment p over denominator increment t end fraction

  • Where:

    • F = force in newtons (N)

    • p = momentum in kilogram metres per second (kg m s-1)

    • t = time in seconds (s)

    • Δ (the Greek letter delta) = change in

  • Change in momentum, Δp, can also be expressed as:

change in momentum = final momentum − initial momentum

increment p space equals space p subscript f i n a l end subscript space minus space p subscript i n i t a l end subscript space equals space p subscript f space minus space p subscript i 

  •  Force and momentum are vector quantities

    • They can have a positive or negative direction

Worked Example

A car of mass 1500 kg hits a wall at an initial velocity of 15 m s-1.

It then rebounds off the wall at 5 m s-1. The car is in contact with the wall for 0.3 s.

Calculate the average force experienced by the car.

Answer:

Step 1: List the known quantities and assign direction:

  • Mass, m = 1500 kg

  • Inital velocity, v subscript i = 15 m s-1

  • Final velocity, v subscript f = −5 m s-1

  • Duration of collision, increment t = 0.3 s

Step 2: State the equation for force and momentum

F space equals space fraction numerator increment p over denominator increment t end fraction

Step 3: State the equation for change in momentum

increment p space equals space p subscript f space minus space p subscript i

Step 4: Calculate the initial momentum

p subscript i space equals space m space cross times space v subscript i

p subscript i space equals space 1500 space cross times space 15 space equals space 22 space 500 space kg space straight m space straight s to the power of negative 1 end exponent

Step 5: Calculate the final momentum

p subscript f space equals space m space cross times space v subscript f

p subscript f space equals space 1500 space cross times space open parentheses negative 5 close parentheses space equals space minus 7500 space kg space straight m space straight s to the power of negative 1 end exponent

Step 6: Calculate the change in momentum

increment p space equals space p subscript f space minus space p subscript i

increment p space equals space minus 7500 space minus space 22 space 500 space equals space minus 30 space 000 space kg space straight m space straight s to the power of negative 1 end exponent

Step 7: Calculate the average force exerted on the car

F space equals space fraction numerator increment p over denominator increment t end fraction

F space equals space fraction numerator negative 30 space 000 over denominator 0.3 end fraction space equals space minus 100 space 000 space straight N

Direction of forces

  • The force that is equal to the rate of change of momentum is still the resultant force

  • The force on an object will be negative if the direction of the force opposes the direction of its initial velocity

  • This means that a force is exerted by the object it has collided with

Forces acting between a car and a wall upon impact

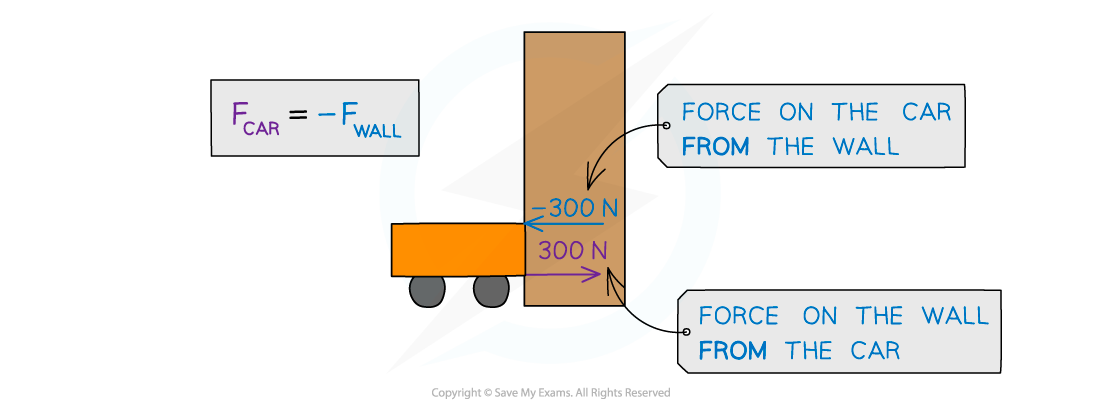
Direction of forces, downloadable AS & A Level Physics revision notes

The force exerted by the wall on car will be equal in magnitude and opposite in direction to the force exerted by the car on the wall: Fcar = –Fwall

 

  • A car collides with a wall, and the car exerts a force of 300 N on the wall

  • The wall also exerts a force of −300 N on the car

  • The force exerted by the wall on the car is equal in magnitude and opposite in direction to the force exerted by the car on the wall

  • This is Newton’s third law of motion (see Newton’s laws of motion)

Time of impact

  • The force exerted is also determined by the time taken for the impact to occur

  • The same change in momentum, over a longer period of time will exert less force, and vice versa

    F space equals space fraction numerator increment p over denominator increment t end fraction

    • As Δt increases, F decreases, when Δp remains the same

    • As Δt decreases, F increases, when Δp remains the same

Worked Example

A tennis player strikes a ball with their racket twice. Each time, the change in momentum of the ball is 0.5 kg m s-1.

During the first strike, the ball is in contact with the racket for 0.2 s. During the second strike, the ball is in contact with the racket for 0.1 s.

Determine which strike the greatest force is exerted on the racket by the ball.

Answer:

Step 1: List the known quantities

  • Change in momentum, Δp = 0.5 kg m s-1

  • Contact time for the first strike, Δt1 = 0.2 s

  • Contact time for the second strike, Δt2 = 0.1 s

Step 2: Determine the force exerted on the racket during the first strike

F subscript 1 space equals space fraction numerator increment p over denominator increment t subscript 1 end fraction

F subscript 1 space equals space fraction numerator 0.5 over denominator 0.2 end fraction space equals space 2.5 space straight N

Step 3: Determine the force exerted on the racket during the second strike

F subscript 2 space equals space fraction numerator increment p over denominator increment t subscript 2 end fraction

F subscript 2 space equals space fraction numerator 0.5 over denominator 0.1 end fraction space equals space 5.0 space straight N

Step 4: State which strike the greatest force is exerted on the racket

  • The ball exerts a greater force on the racket during the second strike

👀 You've read 1 of your 5 free revision notes this week
An illustration of students holding their exam resultsUnlock more revision notes. It's free!

By signing up you agree to our Terms and Privacy Policy.

Already have an account? Log in

Test yourself

Did this page help you?

Previous:Linear MomentumNext:Newton's Laws of Motion
Author
Reviewer
Leander Oates

Author: Leander Oates

Expertise: Physics Content Creator

Leander graduated with First-class honours in Science and Education from Sheffield Hallam University. She won the prestigious Lord Robert Winston Solomon Lipson Prize in recognition of her dedication to science and teaching excellence. After teaching and tutoring both science and maths students, Leander now brings this passion for helping young people reach their potential to her work at SME.

Caroline Carroll

Reviewer: Caroline Carroll

Expertise: Physics & Chemistry Subject Lead

Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.

Download notes on Force & Momentum