Revision NotesExam QuestionsPast Papers
A LevelPhysicsCambridge (CIE)Revision Notes24. Medical PhysicsPET ScanningDetecting Gamma-Rays from PET Scanning

Syllabus Edition

First teaching 2023

First exams 2025

|

Detecting Gamma-Rays from PET Scanning (Cambridge (CIE) A Level Physics)

Revision Note

Ashika

Author

Ashika

Last updated

Calculating energy of gamma-ray photons

  • In the annihilation process, mass, energy and momentum are conserved

  • The gamma-ray photons have an energy and frequency that is determined solely by the mass-energy of the positron-electron pair

  • The energy of a photon is given by:

E space equals space h f space equals space m subscript e c squared

  • The momentum of a photon is given by

space p space equals space fraction numerator space E over denominator c end fraction

  • Where:

    • me = mass of the electron or positron (kg)

    • h = Planck's constant (J s)

    • f = frequency of the photon (Hz)

    • c = the speed of light in a vacuum (m s–1)

Worked Example

Fluorine-18 decays by β+ emission. The positron emitted collides with an electron and annihilates producing two γ-rays.

(a) Calculate the energy released when a positron and an electron annihilate.

(b) Calculate the frequency of the γ-rays emitted.

(c) Calculate the momentum of one of the γ-rays.

Answer:

Part (a)

Step 1: Write down the known quantities

  • Mass of an electron = mass of a positron, me = 9.11 × 10–31 kg

  • Total mass is equal to the mass of the electron and positron = 2me

Step 2: Write out the equation for mass-energy equivalence

E space equals space m subscript e c squared

Step 3: Substitute in values and calculate energy

E space equals space 2 space cross times space open parentheses 9.11 space cross times space 10 to the power of negative 31 end exponent close parentheses space cross times space open parentheses 3.0 space cross times space 10 to the power of 8 close parentheses squared space equals space 1.6 space cross times space 10 to the power of negative 13 end exponent space straight J

Part (b)

Step 1: Determine the energy of one photon

  • Planck's constant, h = 6.63 × 10−34 J s

  • Two photons are produced, so, the energy of one photon is equal to half of the total energy from part (a):

E space equals space fraction numerator 1.6 space cross times space 10 to the power of negative 13 end exponent space over denominator 2 end fraction space equals space 0.8 space cross times space 10 to the power of negative 13 space end exponent straight J

Step 2: Write out the equation for the energy of a photon

E space equals space h f

Step 3: Rearrange for frequency and calculate

f space equals fraction numerator space E over denominator h end fraction space equals space fraction numerator 0.8 space cross times space 10 to the power of negative 13 end exponent space over denominator 6.63 space cross times space 10 to the power of negative 34 end exponent end fraction space equals space 1.2 space cross times space 10 to the power of 20 space Hz

Part (c)

Step 1: Write out the equation for the momentum of a photon

space p space equals fraction numerator space E over denominator c end fraction

Step 2: Substitute in values and calculate momentum

space p space equals fraction numerator space E over denominator c end fraction space equals space fraction numerator 0.8 space cross times space 10 to the power of negative 13 end exponent space over denominator 3.0 space cross times space 10 to the power of 8 end fraction space equals space 2.7 space cross times space 10 to the power of negative 22 end exponent space straight N space straight s

Detecting gamma-rays from PET scanning

  • The patient lays stationary in a tube surrounded by a ring of detectors

  • Images of slices of the body can be taken to show the position of the radioactive tracers

  • The detector consists of two parts:

    • A crystal scintillator

    • A photomultiplier

Crystal scintillator

  • When the gamma-ray (γ-ray) photon is incident on a crystal, an electron in the crystal is excited to a higher energy state

  • As the excited electron travels through the crystal, it excites more electrons

  • When the excited electrons move back down to their original state, the lost energy is transmitted as visible light photons

Photomultiplier

  • The photons produced by the scintillator are very faint

  • Therefore, they need to be amplified and converted to an electrical signal by a photomultiplier tube

PET scanner

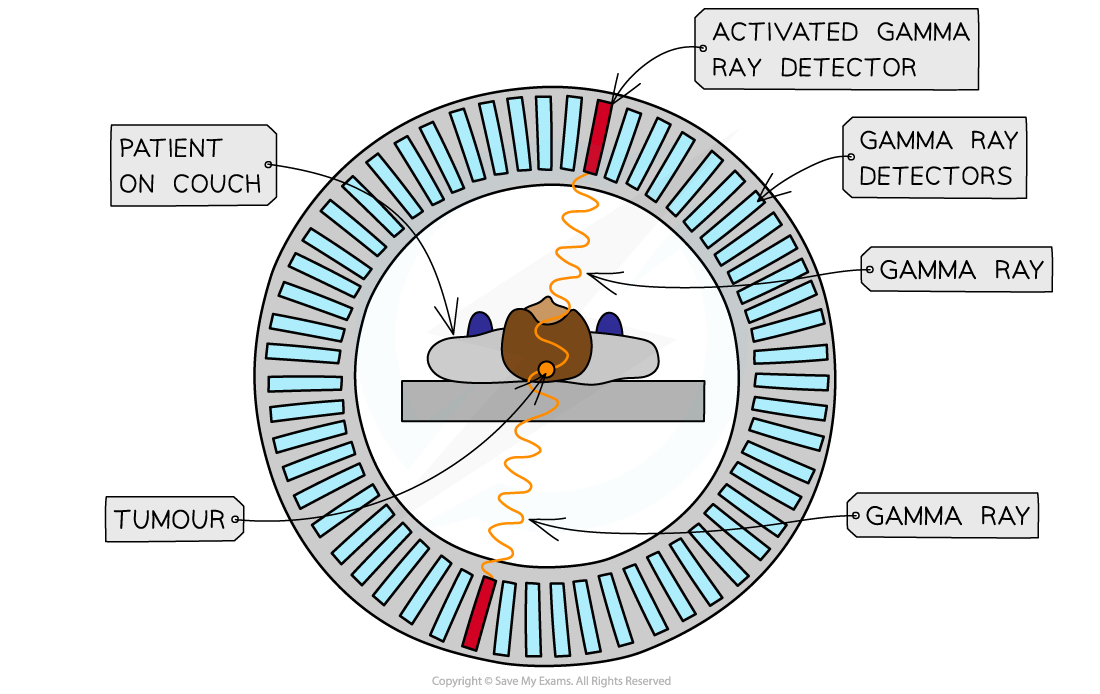
Detecting Gamma Rays, downloadable AS & A Level Physics revision notes

Detecting gamma rays with a PET scanner

Creating an image from PET scanning

  • The γ rays travel in straight lines in opposite directions when formed from a positron-electron annihilation

    • This is due to the conservation of momentum

  • They hit the detectors in a line – known as the line of response

  • The tracers will emit lots of γ rays simultaneously, and the computers will use this information to create an image

  • The more photons formed at a particular point, the more tracer that is present in the tissue being studied, and this will appear as a bright point on the image

  • An image of the tracer concentration in the tissue can be created by processing the arrival times of the gamma-ray photons

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Annihilation in PET ScanningNext:Luminosity & Radiant Flux
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.