Revision NotesExam QuestionsPast Papers
A LevelPhysicsCambridge (CIE)Revision Notes24. Medical PhysicsProduction & Use of UltrasoundAttenuation of Ultrasound in Matter

Syllabus Edition

First teaching 2023

First exams 2025

|

Attenuation of Ultrasound in Matter (Cambridge (CIE) A Level Physics)

Revision Note

Ashika

Author

Ashika

Last updated

Attenuation of ultrasound in matter

  • Attenuation of ultrasound is defined as:

    The reduction of energy due to the absorption of ultrasound as it travels through a material

  • The attenuation coefficient of the ultrasound is expressed in decibels per centimetre lost for every incremental increase in megahertz frequency

    • Generally, 0.5 dB cm–1 is lost for every 1 MHz

  • The intensity I of the ultrasound decreases with distance x, according to the equation:

I space equals space I subscript 0 e to the power of negative mu x end exponent

  • Where:

    • I0 = the intensity of the incident beam (W m-2)

    • I = the intensity of the reflected beam (W m-2)

    • μ = the absorption coefficient (m-1)

    • x = distance travelled through the material (m)

  • The absorption coefficient μ, will vary from material to material

  • Attenuation is not a major problem in ultrasound scanning as the scan relies on the reflection of the ultrasounds at the boundaries of materials

Intensity-depth graph showing attenuation

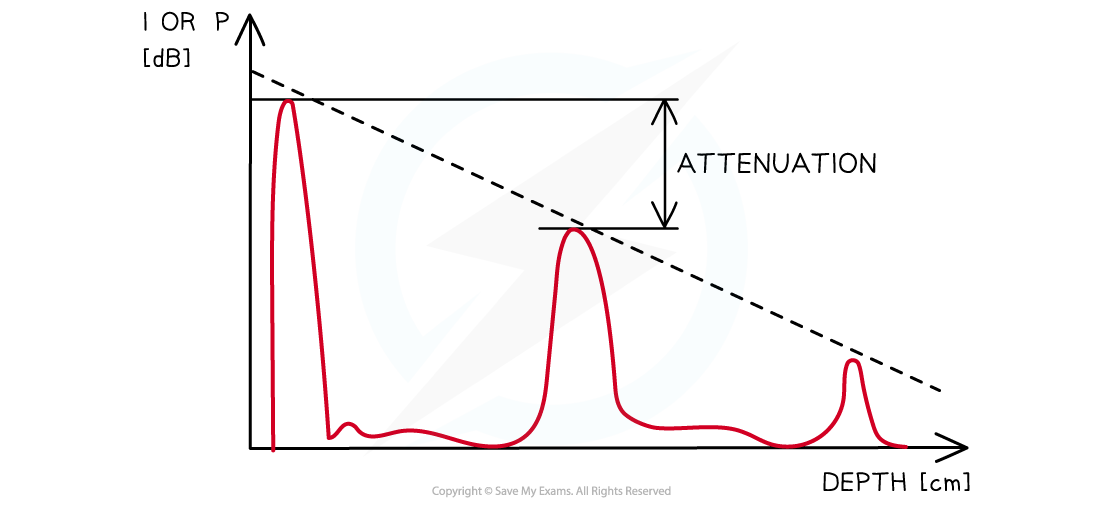
Attenuation of Ultrasound Graph, downloadable AS & A Level Physics revision notes

When the intensity is expressed in decibels, the amplitudes of the echoes can be seen to decrease linearly

Worked Example

The thickness x of the layer of fat on an animal, as shown in the diagram, is to be investigated using ultrasound.

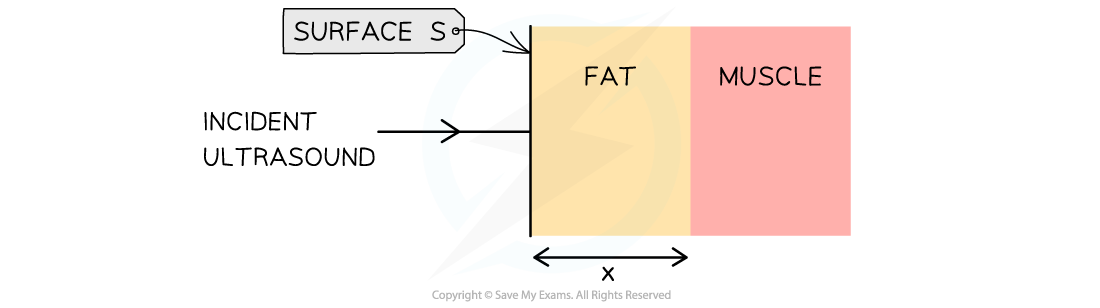
WE - Attenuation of Ultrasound question image, downloadable AS & A Level Physics revision notes

The intensity of the parallel ultrasound beam entering the surface S of the layer of fat is I.

The beam is reflected from the boundary between fat and muscle.

The intensity of the reflected ultrasound detected at the surface S of the fat is 0.012 I.

Medium

Z / kg m–2 s–1

μ / m–1

Fat

1.3 × 106

48

Muscle

1.7 × 106

23

Using the information in the table, calculate:

(a) The intensity reflection coefficient at the boundary between the fat and the muscle.

(b) The thickness x of the layer of fat. 

Answer:

Part (a)

Step 1: Write down the equation for intensity reflection coefficient α

alpha space equals space fraction numerator open parentheses Z subscript 2 space minus space Z subscript 1 close parentheses squared space over denominator open parentheses Z subscript 2 space thin space plus thin space Z subscript 1 close parentheses squared end fraction

Step 2: Calculate the intensity reflection coefficient

alpha space equals space fraction numerator open parentheses 1.7 space cross times space 10 to the power of 6 space minus space 1.3 space cross times space 10 to the power of 6 close parentheses squared space over denominator open parentheses 1.7 space cross times space 10 to the power of 6 space space plus thin space 1.3 space cross times space 10 to the power of 6 close parentheses squared end fraction space equals space fraction numerator open parentheses 0.4 close parentheses squared space over denominator open parentheses 3 close parentheses squared end fraction space equals space 0.018

  • This means that 0.018 of the intensity is reflected at the interface between fat and muscle

  • This reflected intensity will move back through the fat towards surface S

Part (b)

Step 1: Write out the known quantities

  • The intensity of the ultrasound pulse is affected 3 times:

    • Attenuation from the surface S to the fat-muscle boundary

    • Reflection at the boundary

    • Attenuation from the boundary back to the surface S

  • After being transmitted in the fat, the intensity at surface S is given to be 0.012 I.

  • Therefore, the intensity is 0.018 I at the fat-muscle boundary, and as the ultrasound moves through the fat, it gets attenuated and the new intensity at the surface S is now 0.012 I

incident intensity = intensity of the reflected pulse

I subscript 0 space equals space 0.018 I e to the power of negative mu x end exponent

  • Transmitted intensity = 0.012 I

  • Absorption coefficient, mu = 48 m-1

  • Thickness of fat = x

Step 2: Write out the equation for attenuation

I space equals space I subscript 0 e to the power of negative mu x end exponent

Step 3: Substitute in values for intensity and simplify

0.012 I space equals space open parentheses 0.018 I space cross times space e to the power of negative mu x end exponent close parentheses space cross times space e to the power of negative mu x end exponent

0.012 space equals space 0.018 e to the power of negative 2 mu x end exponent

Step 4: Rearrange and take the natural log of both sides

fraction numerator 0.012 over denominator 0.018 end fraction space equals space e to the power of negative 2 mu x end exponent

ln open parentheses fraction numerator 0.012 over denominator 0.018 end fraction close parentheses space equals space minus 2 mu x

Step 5: Rearrange and calculate the thickness x

x space equals space fraction numerator ln open parentheses fraction numerator 0.012 over denominator 0.018 end fraction close parentheses space over denominator negative 2 mu end fraction space equals space fraction numerator ln open parentheses fraction numerator 0.012 over denominator 0.018 end fraction close parentheses space over denominator negative 2 space cross times space 48 end fraction space equals space 4.22 space cross times space 10 to the power of negative 3 end exponent space straight m space equals space 0.42 space cm

Examiner Tips and Tricks

The intensity equation will not be provided for you on your exam datasheet, so make sure you remember this!

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Intensity Reflection CoefficientNext:Production & Use of X-rays
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.