Mass Defect & Binding Energy (Cambridge (CIE) A Level Physics)

Mass defect & binding energy

Mass defect

• Experiments into nuclear structure have found that the total mass of a nucleus is less than the sum of the masses of its constituent nucleons

• This difference in mass is known as the mass defect

• Mass defect is defined as:

  The difference between the mass of a nucleus and the sum of the individual masses of its protons and neutrons

• The mass defect Δm of a nucleus can be calculated using:

Δm = Zm_p + (A – Z)m_n – m_total

• Where:

  • Z = proton number

  • A = nucleon number

  • m_p = mass of a proton (kg)

  • m_n = mass of a neutron (kg)

  • m_total = measured mass of the nucleus (kg)

Mass defect of carbon-12

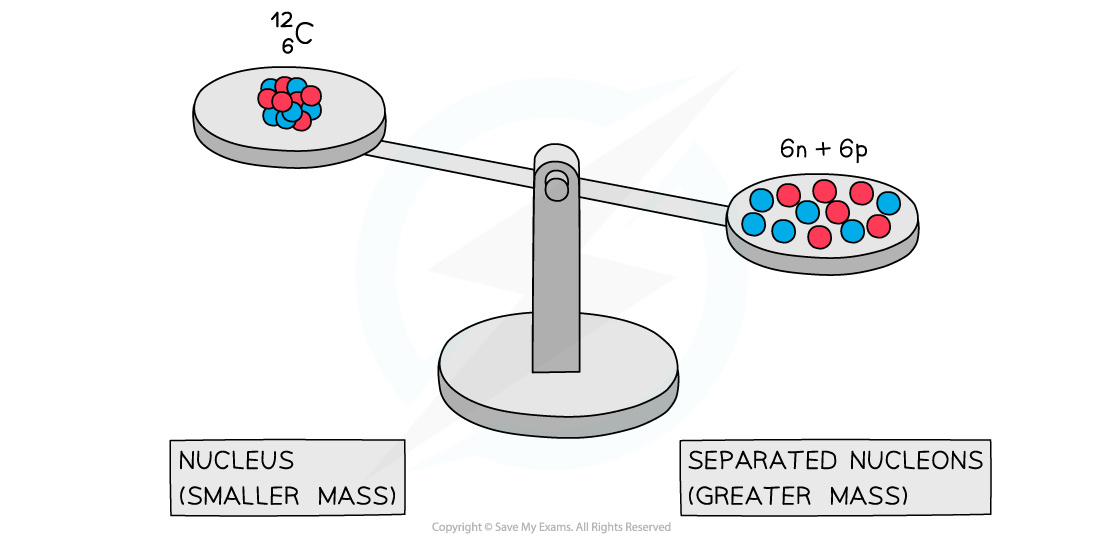
A system of separated nucleons has a greater mass than a system of bound nucleons

• Due to the equivalence of mass and energy, this decrease in mass implies that energy is released in the process

• Since nuclei are made up of neutrons and protons, there are forces of repulsion between the positive protons

  • Therefore, it takes energy, ie. the binding energy, to hold nucleons together as a nucleus

Binding energy

• Binding energy is defined as:

  The energy required to break a nucleus into its constituent protons and neutrons

• Energy and mass are proportional, so, the total energy of a nucleus is less than the sum of the energies of its constituent nucleons

• The formation of a nucleus from a system of isolated protons and neutrons is therefore an exothermic reaction

  • This means that it releases energy

• This energy can be calculated using the equation:

E = Δmc²

• In a typical nucleus, binding energies are usually measured in MeV

  • This is considerably larger than the few eV associated with the binding energy of electrons in the atom

• Nuclear reactions involve changes in the nuclear binding energy whereas chemical reactions involve changes in the electron binding energy

  • This is why nuclear reactions produce much more energy than chemical reactions

Binding energy per nucleon

• In order to compare nuclear stability, it is more useful to look at the binding energy per nucleon

• The binding energy per nucleon is defined as:

  The binding energy of a nucleus divided by the number of nucleons in the nucleus

• A higher binding energy per nucleon indicates a higher stability

  • In other words, more energy is required to separate the nucleons contained within a nucleus

Graph of binding energies for nuclei of different masses

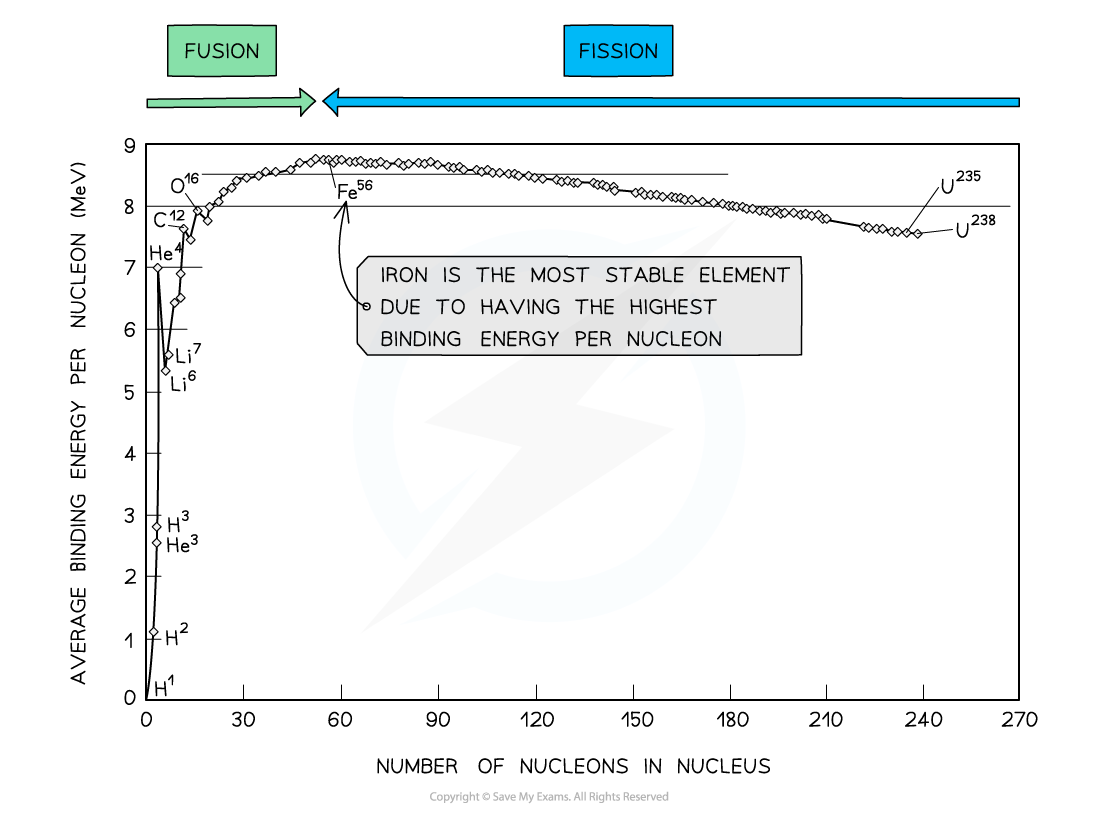
By plotting a graph of binding energy per nucleon against nucleon number, the stability of elements can be inferred

Key features of the graph

• At low values of A:

  • Nuclei have lower binding energies per nucleon than at large values of A, but they tend to be stable when N = Z

  • This means light nuclei have weaker electrostatic forces and will undergo fusion

  • The gradient is much steeper compared to the gradient at large values of A

  • This means that fusion reactions release a greater binding energy than fission reactions

• At high values of A:

  • Nuclei have generally higher binding energies per nucleon, but this gradually decreases with A

  • This means the heaviest elements are the most unstable and will undergo fission

  • The gradient is less steep compared to the gradient at low values of A

  • This means that fission reactions release less binding energy than fission reactions

• Iron (A = 56) has the highest binding energy per nucleon, which makes it the most stable of all the elements

• Helium (⁴He), carbon (¹²C) and oxygen (¹⁶O) do not fit the trend

  • Helium-4 is a particularly stable nucleus hence it has a high binding energy per nucleon

  • Carbon-12 and oxygen-16 can be considered to be three and four helium nuclei, respectively, bound together