Revision NotesExam QuestionsPast Papers
A LevelPhysicsCIERevision Notes22. Quantum Physics22.4 Energy Levels in Atoms & Line SpectraCalculating Discrete Energies

Syllabus Edition

First teaching 2023

First exams 2025

|

Calculating Discrete Energies (CIE A Level Physics)

Revision Note

Ashika

Author

Ashika

Last updated

Calculating Discrete Energies

  • The difference between two energy levels is equal to a specific photon energy
  • This difference is energy is calculated by the equation:

increment E space equals space h f space equals space E subscript 2 space minus space E subscript 1

  • Where,
    • E1 = energy of the lower level (J)
    • E2 = energy of the higher level (J)
    • h = Planck’s constant (J s)
    • f = frequency of photon (Hz)

     

  • Using the wave equation, the wavelength of the emitted, or absorbed, radiation can be related to the energy difference by the equation:

lambda space equals space fraction numerator space h c over denominator E subscript 2 space minus space E subscript 1 end fraction

  • This equation shows that the larger the difference in energy of two levels ΔE, the shorter the wavelength λ and vice versa

Worked example

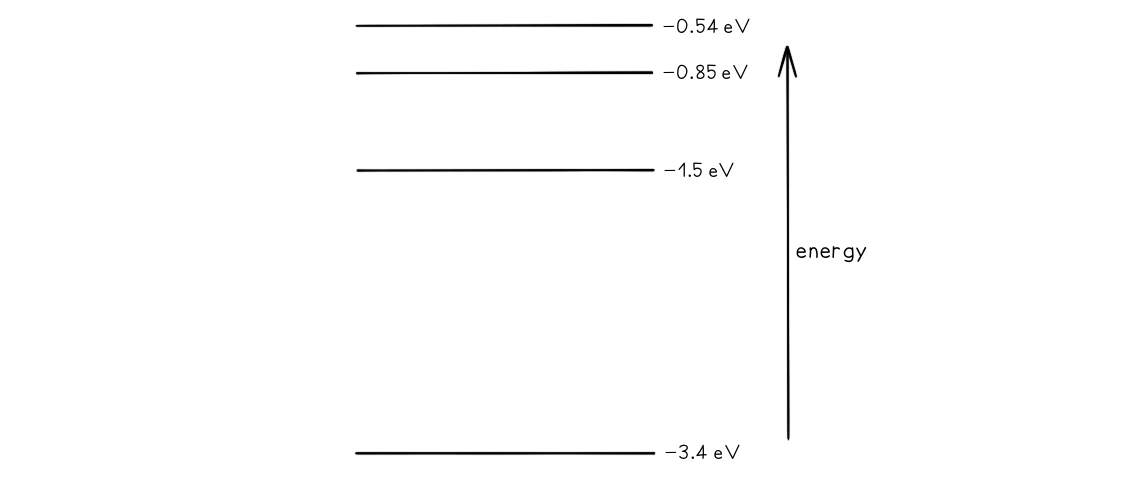
Some electron energy levels in atomic hydrogen are shown below.WE - Calculating Discrete Energies Question, downloadable AS & A Level Physics revision notesThe longest wavelength produced as a result of electron transitions between two of the energy levels is 4.0 × 10–6 m.

a) Draw and mark:

  • The transition giving rise to the wavelength of 4.0 × 10–6 m with letter L.
  • The transition giving rise to the shortest wavelength with letter S.

b) Calculate the wavelength for the transition giving rise to the shortest wavelength.

Answer:

Part (a)

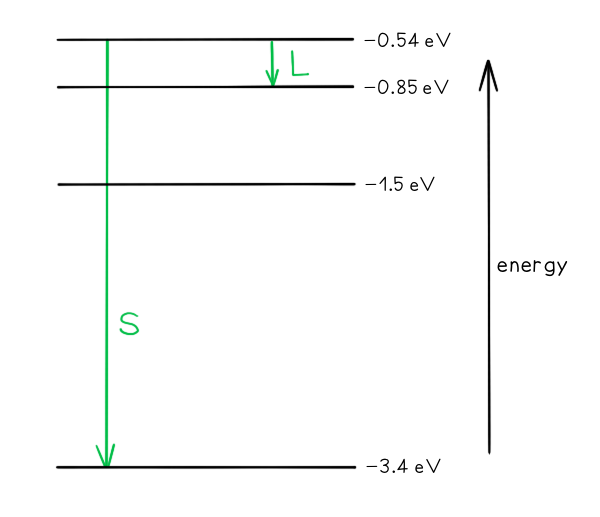
Calculating-Discrete-Energies-Worked-Example---Calculating-Discrete-Energies-Answer, downloadable AS & A Level Physics revision notes

  • Photon energy and wavelength are inversely proportional, so the largest energy change corresponds to the shortest wavelength (line S) and the smallest energy change corresponds to the longest wavelength (line L)

Part (b)

Step 1: Write down the equation linking the wavelength and the energy levels

lambda space equals space fraction numerator space h c over denominator E subscript 2 space minus space E subscript 1 end fraction

Step 2: Identify the energy levels giving rise to the shortest wavelength

  • E1 = –0.54 eV
  • E2 = –3.4 eV

Step 3: Calculate the wavelength

  • To convert from eV → J: multiply by 1.6 × 10-19

lambda space equals space fraction numerator open parentheses 6.63 space cross times space 10 to the power of negative 34 end exponent close parentheses open parentheses 3 space cross times space 10 to the power of 8 close parentheses space over denominator open parentheses negative 3.4 space minus space open parentheses negative 0.54 close parentheses close parentheses open parentheses 1.6 space cross times space 10 to the power of negative 19 end exponent close parentheses end fraction space equals space open parentheses minus close parentheses 4.347 space cross times space 10 to the power of negative 7 end exponent space straight m space equals space 435 space nm

Examiner Tip

Don't forget the minus sign and correctly know which energy level is E2 and E1. 

The equation for ΔE gives the value of energy in joules. Therefore, if the energy has been given in eV, you have to convert this into joules for the calculations.

Although you may get a negative wavelength, the minus sign is not as important, but the value of the wavelength is for full marks.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Line SpectraNext:Energy & Mass Equivalence
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.