Force on a Current-Carrying Conductor (CIE A Level Physics)

• The force F on a conductor carrying current I at an angle θ to a magnetic field with flux density B is defined by the equation

• Where:
  • F = force on a current-carrying conductor in a B field (N)
  • B = magnetic flux density of applied B field (T)
  • I = current in the conductor (A)
  • L = length of the conductor (m)
  • θ = angle between the conductor and applied B field (degrees)

• This equation shows that the force on the conductor can be increased by:
  • increasing the strength of the magnetic field
  • increasing the current flowing through the conductor
  • increasing the length of the conductor in the field

• Note: The length L represents the length of the conductor that is within the field

Magnetic force on a current-carrying conductor

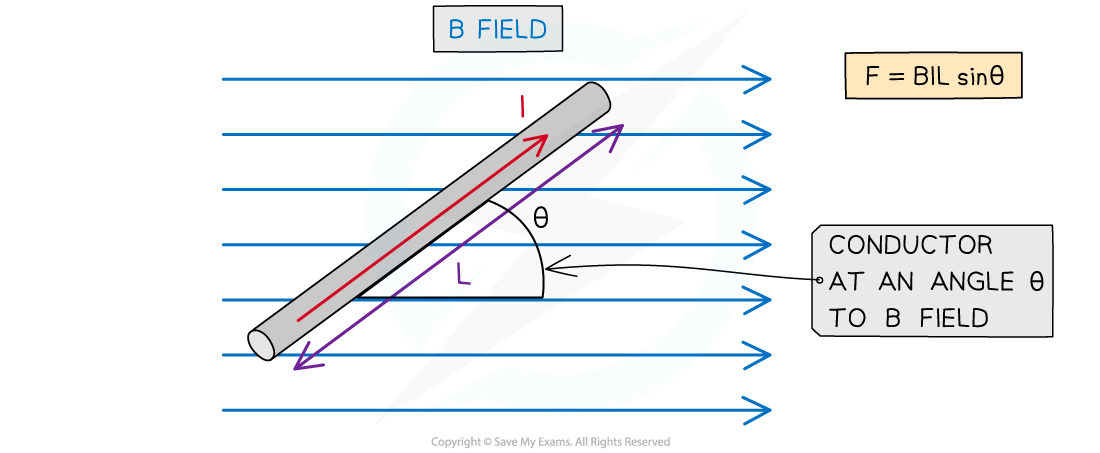
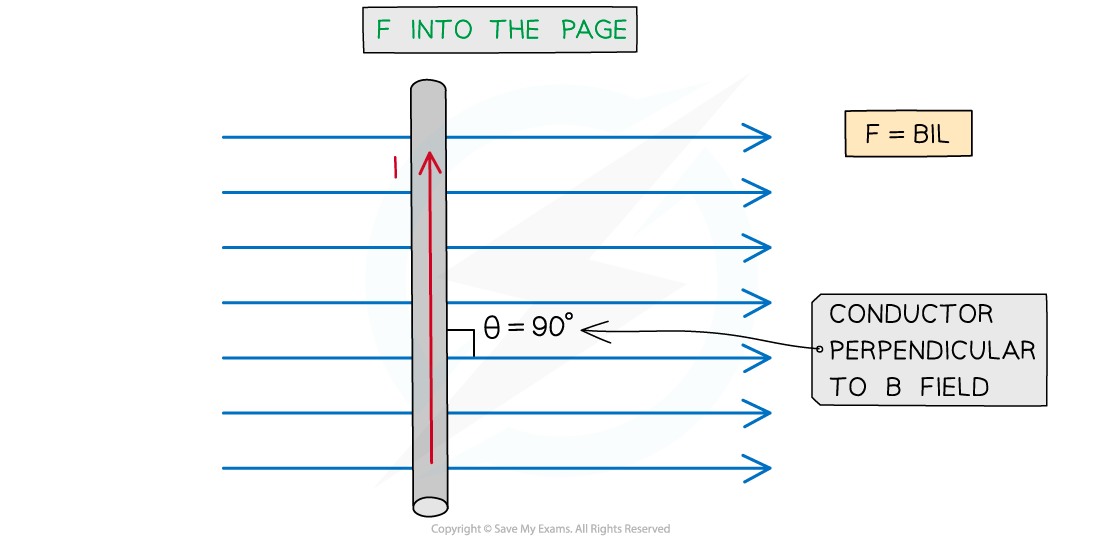
The magnitude of the force on a current-carrying conductor depends on the angle of the conductor to the external B field

• A current-carrying conductor (e.g. a wire) will experience the maximum magnetic force if the current through it is perpendicular to the direction of the magnetic field lines
  • It experiences no force if it is parallel to magnetic field lines

• The maximum force occurs when sin θ = 1
  • This means θ = 90° and the conductor is perpendicular to the B field

• The equation for the magnetic force becomes:

• The minimum force, i.e. F = 0 N, is when sin θ = 0°
  • This means θ = 0° and the conductor is parallel to the B field

• It is important to note that a current-carrying conductor will experience no force if the current in the conductor is parallel to the field
  • This is because the F, B and I must be perpendicular to each other