Area under a Velocity-Time Graph (CIE A Level Physics)

Revision Note

Test yourself

Author

Ashika

Last updated

15 October 2024

Area under a velocity-time graph

Velocity-time graphs show the speed and direction of an object in motion over a specific period of time
The area under a velocity-time graph is equal to the displacement of a moving object

The area under a graph can be sectioned into triangles and rectangles to make the calculations easier
The area of a triangle can be found with the following formula:

$A_{t r i a n g l e} = \frac{1}{2} b h$

The area of a rectangle can be found with the following formula:

$A_{r e c t a n g l e} = b h$

Where:
- $A$ = area
- $b$ = length of base
- $h$ = height

Worked example

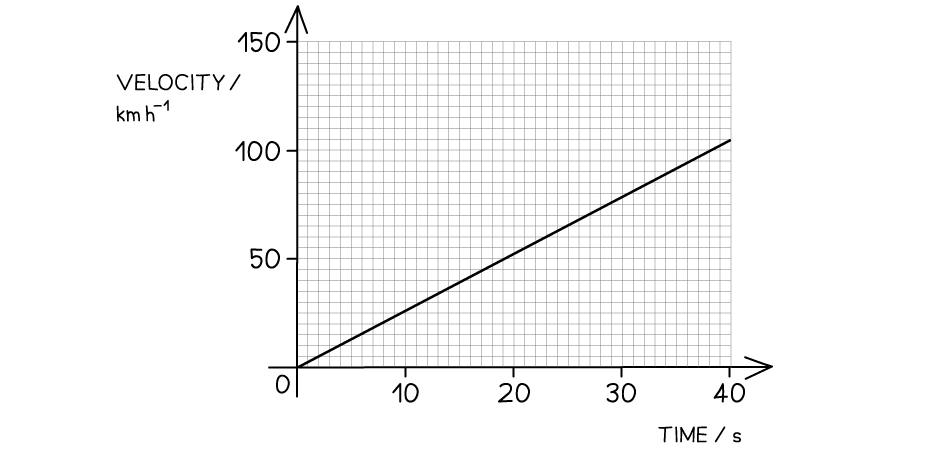
The velocity-time graph of a vehicle travelling with uniform acceleration is shown in the diagram below. v-t Area Worked Example (1), downloadable AS & A Level Physics revision notes

Calculate the displacement of the vehicle at 40 s.

Answer:

Step 1: State how to determine the displacement

The displacement is equal to the area under a velocity-time graph

Step 2: Determine the scale on the graph

Each division is $\frac{50}{10} = 5 km h^{- 1}$

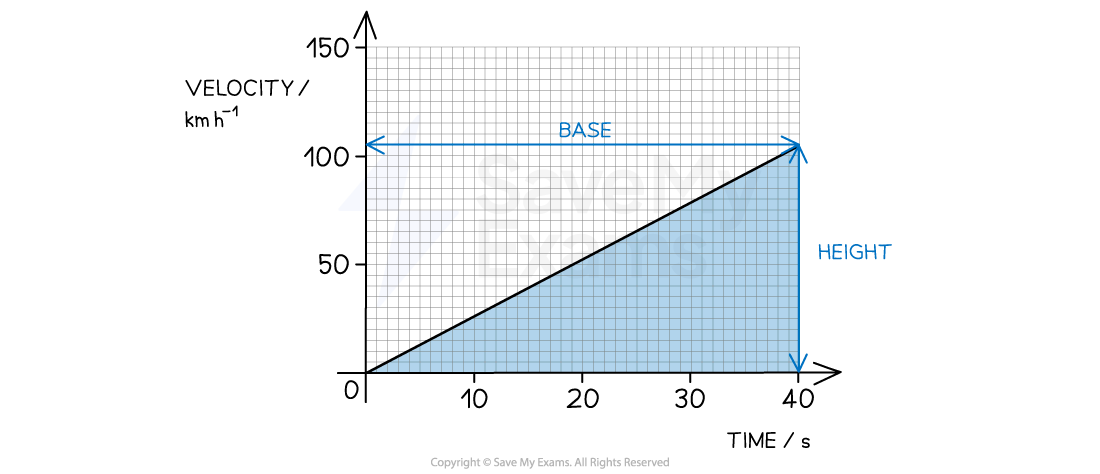
2-1-3-we-v-t-answer-cie-new

Step 3: Determine the base and height of the graph

Time = base = 40 s
Velocity = height = 105 km h^–1

Step 4: Convert km h^-1 into km s^–1

$\frac{105}{60 \times 60} = 0.0292 km s^{- 1}$

Step 5: Calculate the area under the graph

Area of a right-angled triangle = $\frac{1}{2} \times b a s e \times h e i g h t$

$A r e a = \frac{1}{2} \times 40 \times 0.0292 = 0.6 km$

Examiner Tip

Always check the values given on the y-axis of a motion graph - students often confuse displacement-time graphs and velocity-time graphs.

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?

Author: Ashika

Expertise: Physics Project Lead

Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.