Area Under a Potential–Charge Graph

When charging a capacitor, the power supply transfers electrons onto one plate, giving it a negative charge, and transfers electrons away from the other plate, giving it a positive charge
- It therefore does work on the electrons, which increases their electric potential energy

At first, a small amount of charge is pushed onto the negative plate, then gradually, this builds up
- Adding more electrons to the plate is relatively easy at first since there is little repulsion

As the charge of the negative plate increases i.e. becomes more negatively charged, the electric repulsion between the electrons increases
- This means a greater amount of work must be done to increase the charge on the negative plate

Charging a capacitor

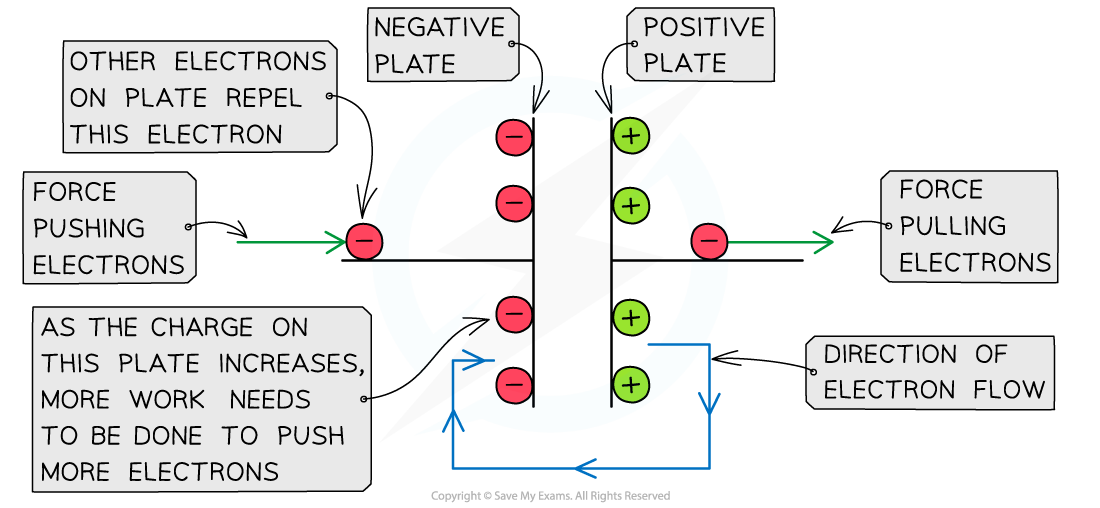
Charge on capacitor plates, downloadable AS & A Level Physics revision notes

As the charge on the negative plate builds up, more work needs to be done to add more charge

The relationship between the potential difference and charge on a capacitor is:

The potential difference V across the capacitor increases as the amount of charge Q increases

In other words, the charge Q on the capacitor is directly proportional to its potential difference V
- The graph of charge against potential difference is therefore a straight-line graph through the origin

Therefore, the electric potential energy stored in the capacitor can be determined from the area under the potential-charge graph

Graph of potential difference against charge

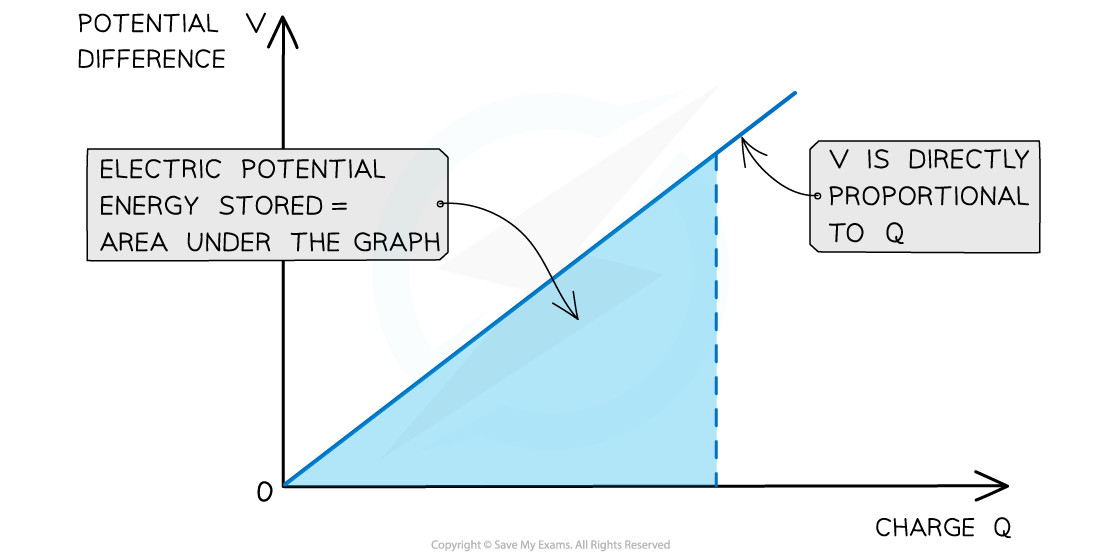
EPE energy on graph, downloadable AS & A Level Physics revision notes

The electric potential energy stored in the capacitor is the area under the potential-charge graph

Worked example

The variation of the potential V of a charged isolated metal sphere with surface charge Q is shown on the graph below. WE Area under a Potential–Charge question graph, downloadable AS & A Level Physics revision notes

Using the graph, determine the electric potential energy stored on the sphere when charged to a potential of 100 kV.

Answer:

Step 1: Determine the charge on the sphere at the potential of 100 kV

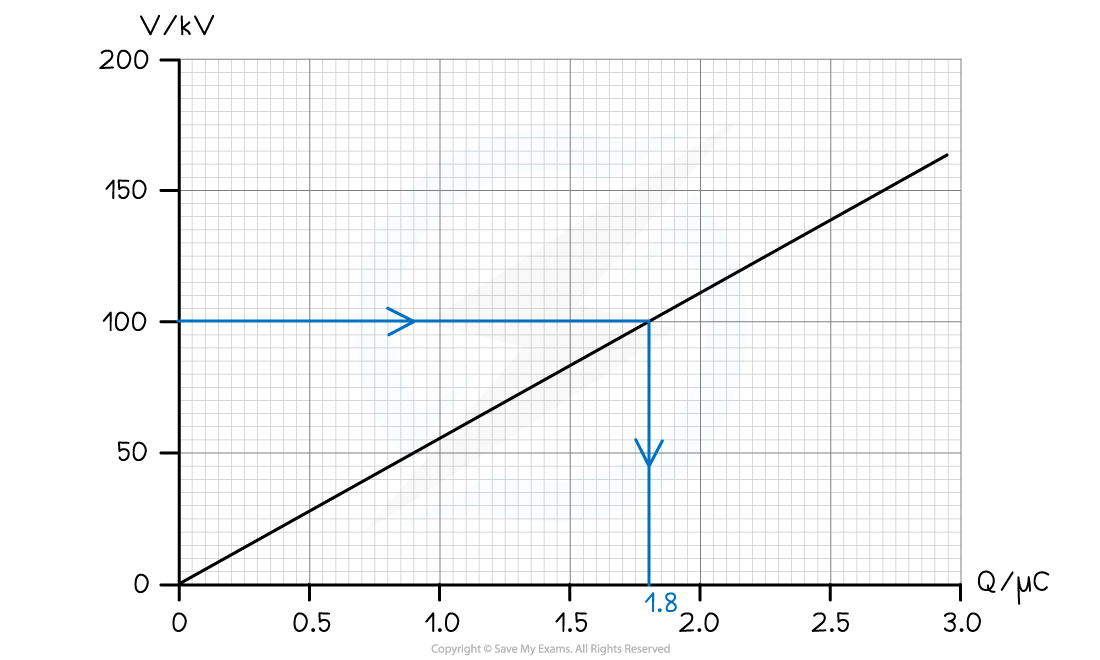
WE Area under a Potential–Charge solution graph, downloadable AS & A Level Physics revision notes

From the graph, the charge on the sphere at 100 kV is 1.8 μC

Step 2: Calculate the electric potential energy stored

The electric potential energy stored is equal to the area under the graph up to 100 kV
Using the area of a triangle:

$Area = \frac{1}{2} \times base \times height$

Substituting the values into the equation gives:

$Area = \frac{1}{2} \times 1.8 μC \times 100 kV$

$EPE = \frac{1}{2} \times (1.8 \times 10^{- 6}) \times (100 \times 10^{3}) = 0.09 J$

Examiner Tip

Remember to always check the units of the charge–potential difference graphs. The charges can often be in µC or the potential difference in kV! The units must be in C and V to get a work done in J.

Area Under a Potential–Charge Graph (CIE A Level Physics)

Revision Note