Capacitors in Series & Parallel (Cambridge (CIE) A Level Physics)

Capacitors in series & parallel

• The combined capacitance of capacitors in a circuit depends on whether they are connected in series or parallel

Capacitors in series

• Consider two parallel plate capacitors C₁ and C₂ connected in series, with a potential difference (p.d) V across them

Potential difference of capacitors in series

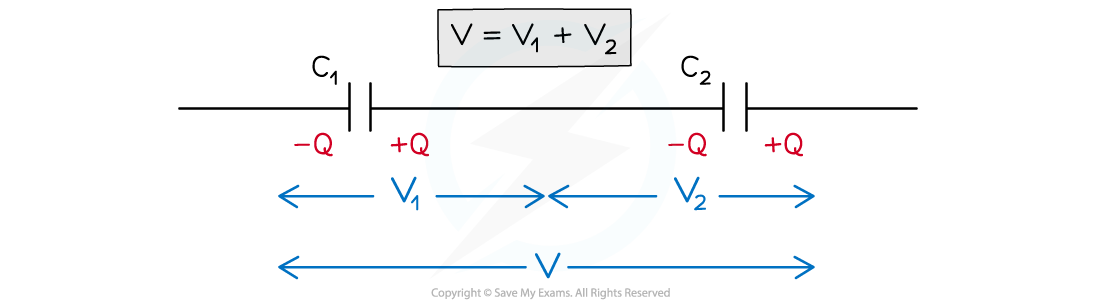
Capacitors connected in series have different p.d across them but have the same charge

• In a series circuit, p.d. is shared between all the components in the circuit

  • Therefore, if the capacitors store the same charge on their plates but have different p.d.s, the p.d across C₁ is V₁ and across C₂ is V₂

• The total potential difference V is the sum of V₁ and V₂

V = V₁ + V₂  

• Rearranging the capacitance equation for the p.d. V means V₁ and V₂ can be written as:

and 

• Where the total p.d. V is defined by the total capacitance

• Substituting these into the equation V = V₁ + V₂ equals:

• Since the current is the same through all components in a series circuit, the charge Q is the same through each capacitor and cancels out

• Therefore, the equation for the combined capacitance of capacitors in series is:

Capacitors in parallel

• Consider two parallel plate capacitors C₁ and C₂ connected in parallel, each with p.d, V

Potential difference of capacitors in parallel

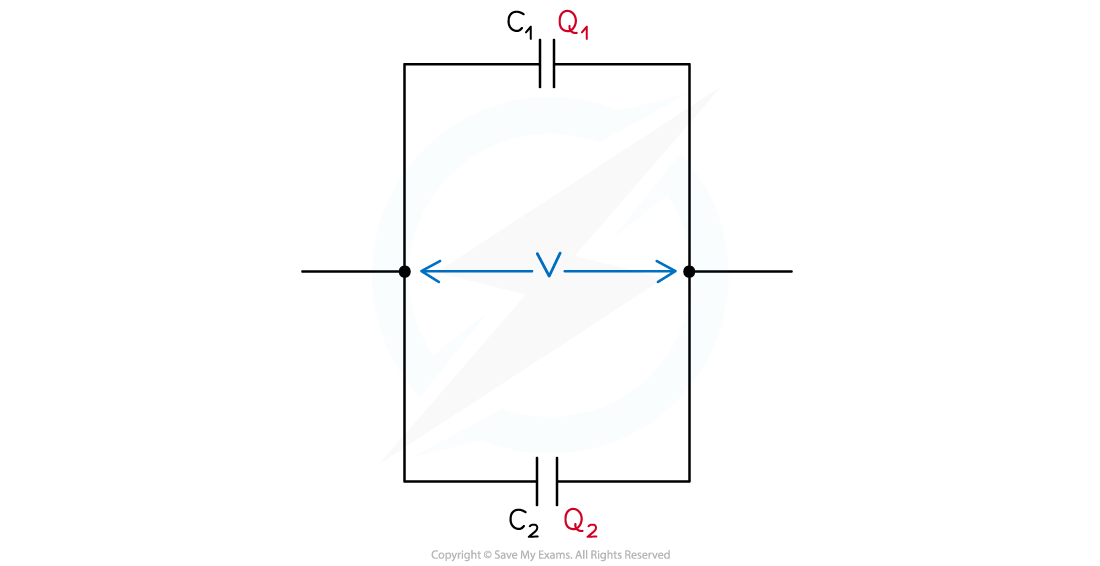
Capacitors connected in parallel have the same p.d across them, but different charge

• Since the current is split across each junction in a parallel circuit, the charge stored on each capacitor is different

  • Therefore, the charge on capacitor C₁ is Q₁ and on C₂ is Q₂

• The total charge Q is the sum of Q₁ and Q₂

Q = Q₁ + Q₂

• Rearranging the capacitance equation for the charge Q means Q₁ and Q₂ can be written as:

Q₁ = C₁V and Q₂ = C₂V

• Where the total charge Q is defined by the total capacitance:

Q = C_totalV

• Substituting these into the Q = Q₁ + Q₂ equals:

C_totalV = C₁V + C₂V = (C₁ + C₂) V

• Since the p.d is the same across all components in each branch of a parallel circuit, the p.d V cancels out

• Therefore, the equation for the combined capacitance of capacitors in parallel is:

C_total = C₁ + C₂ + C₃ ...