Capacitance (Cambridge (CIE) A Level Physics)

Defining capacitance

• Capacitors are electrical devices used to store energy

  • In electronic circuits, they are commonly used as a backup store of energy in case of power failure

• The circuit symbol for a parallel plate capacitor is two parallel lines

Capacitor circuit symbol

The circuit symbol for a capacitor consists of two parallel lines perpendicular to the wires on either side  

• Capacitors possess capacitance, which is defined as:

  The charge stored per unit potential

• The greater the capacitance, the greater the charge stored on the capacitor

• Capacitors come in different forms, such as:

  • isolated spherical conductors

  • parallel plates

Isolated spherical conductors

• An isolated spherical conductor can store charge on its surface, which means it can act as a capacitor

• When the conducting sphere is connected to a high-voltage supply:

  • electrons move on to, or off of, the surface of the sphere 

  • the remaining charges are of the same type, so they repel

  • the surface is conducting, allowing them to move and become evenly distributed

• As the potential difference of the supply increases, the charge on the conductor also increases

• The capacitance of the sphere is equal to the ratio of the charge to the potential

Capacitance of an isolated spherical conductor

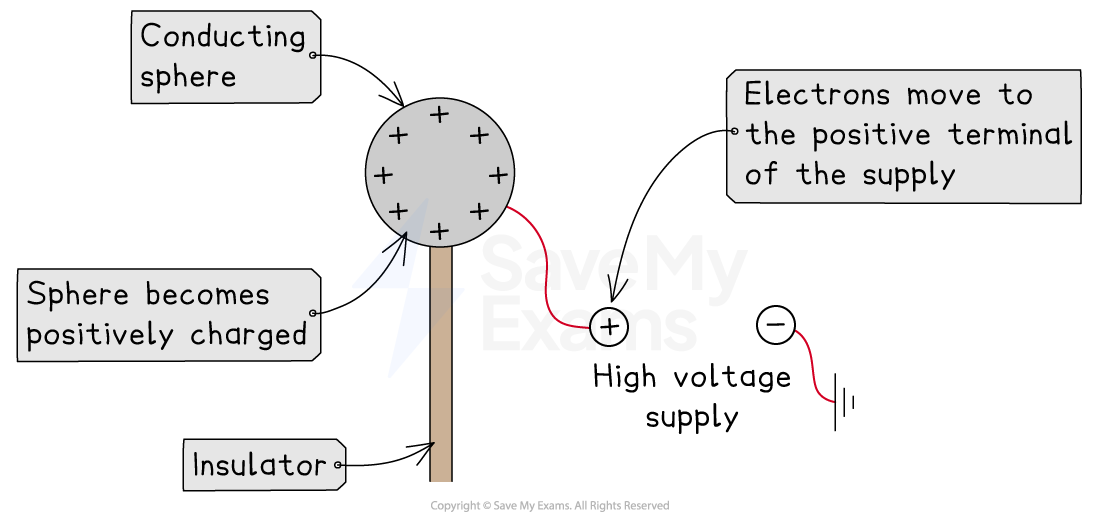
Conducting spheres act like capacitors due to their ability to store charge on their surfaces

Parallel plate capacitors

• A parallel plate capacitor is made up of two conducting metal plates connected to a voltage supply

  • The negative terminal of the voltage supply pushes electrons onto one plate, making it negatively charged

  • The electrons are repelled from the opposite plate, making it positively charged

  • There is a dielectric between the plates which ensures charge does not flow freely between the plates

Capacitance of a parallel plate capacitor

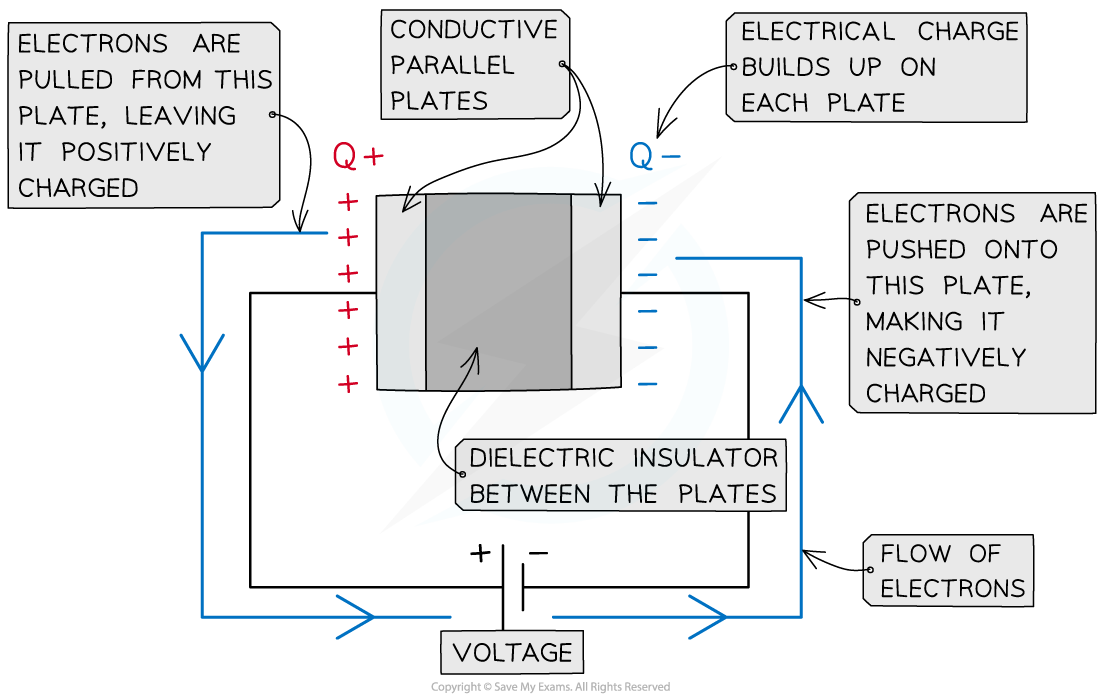
A parallel plate capacitor is made up of two conductive plates with opposite charges building up on each plate

Calculating capacitance

• The capacitance of a capacitor is defined by the equation:

• Where:

  • C = capacitance (F)

  • Q = charge (C)

  • V = potential difference (V)

• The unit of capacitance is the farad (F), where one farad is equivalent to one coulomb per volt

  • In practice, 1 F, or 1 C V^–1, is a very large unit

  • As a result, capacitance values are often quoted in microfarads (μF), nanofarads (nF) or picofarads (pF)

A typical capacitor

A capacitor of capacitance 47 μF might typically be used in a simple circuit

• For a parallel plate conductor, Q is the charge on the plates and V is the potential difference across the capacitor

  • Note: The charge Q is not the charge of the capacitor itself, it is the charge stored on the plates

• This capacitance equation shows that an object’s capacitance is the ratio of the charge on an object to its potential

Capacitance of a spherical conductor

• The capacitance of an isolated spherical conductor is equal to the charge per unit potential at the surface of the sphere

  • This is because the charge on the surface of a spherical conductor can be considered as a point charge at its centre

• The potential V of an isolated point charge is given by:

• Where:

  • R = radius of the sphere (m)

  • ε₀ = permittivity of free space

• Combining these equations gives an expression for the capacitance of an isolated spherical conductor:

C = 4πε₀R

• Note: The charge Q is not the charge of the capacitor itself, it is the charge stored on the surface of the spherical conductor