Revision NotesExam QuestionsPast Papers
A LevelPhysicsCIERevision Notes18. Electric Fields18.4 Electric Field of a Point ChargeElectric Field Strength of a Point Charge

Syllabus Edition

First teaching 2023

First exams 2025

|

Electric Field Strength of a Point Charge (CIE A Level Physics)

Revision Note

Ann H

Author

Ann H

Last updated

Electric field of a point charge

  • The strength of an electric field due to a point charge decreases with the square of the distance
    • This is an inverse square law, similar to Coulomb's law
  • Using Coulomb's law and the electric field strength equation this can be written as:

E space equals space F over q space equals space fraction numerator Q over denominator 4 straight pi epsilon subscript 0 r squared end fraction

  • Where:
    • Q = the point charge producing the radial electric field (C)
    • r = distance from the centre of the charge (m)
    • ε0 = permittivity of free space (F m−1)
  • Here, q represents the magnitude of a small positive test charge
  • This equation shows that in a radial electric field, the electric field strength E:
    • is not constant
    • follows an inverse square law with distance r
  • This equation is analogous to the gravitational field strength around a point mass

Graph of field strength against distance for a positive charge

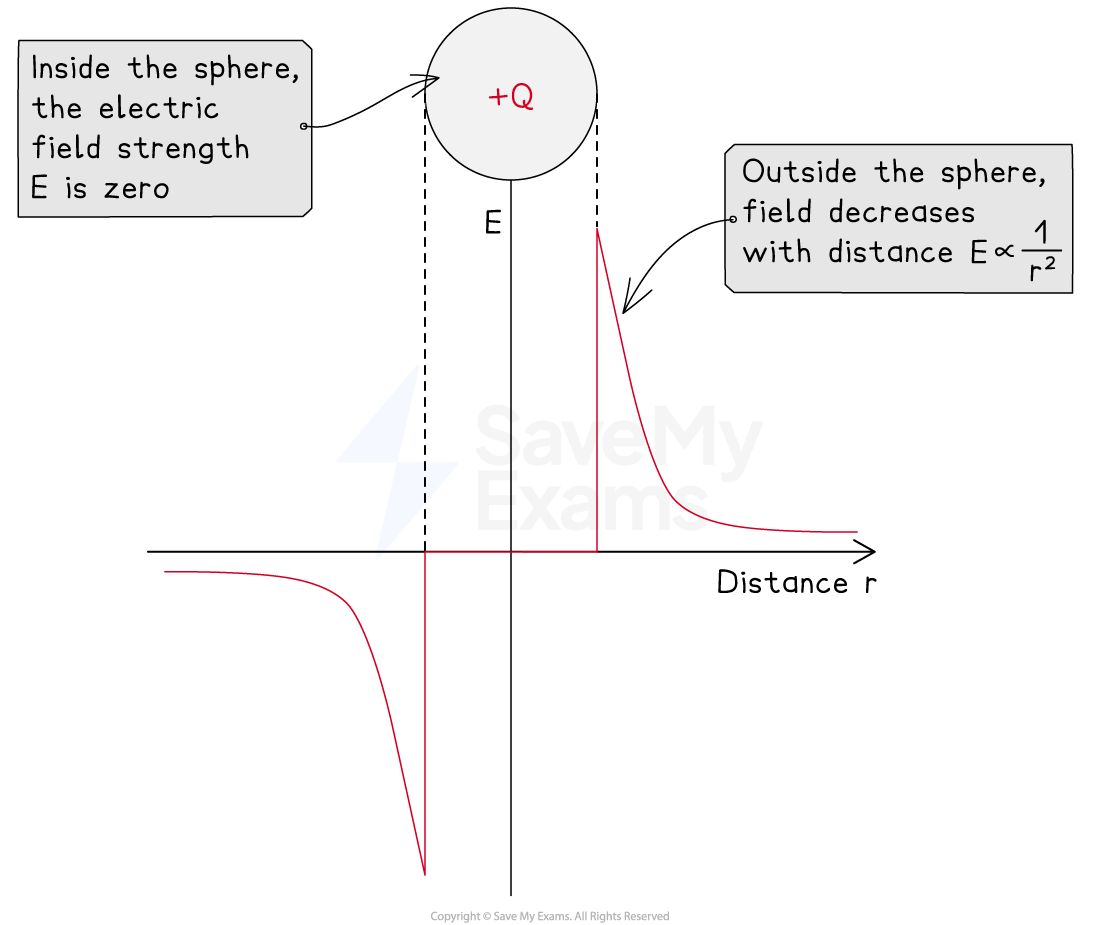
4-2-6-electric-field-around-charged-sphere

Electric field strength is zero inside a charged sphere and decreases with distance outside the sphere according to an inverse square law

Combining electric fields

  • Both electric force and field strength are vector quantities
    • If the charge is negative, the E field strength is negative and points towards the centre of the charge
    • If the charge is positive, the E field strength is positive and points away from the centre of the charge
  • Therefore, to find the electric force or field strength at a point due to multiple charges, each field can be combined by vector addition

Vector addition of electric field along the same line

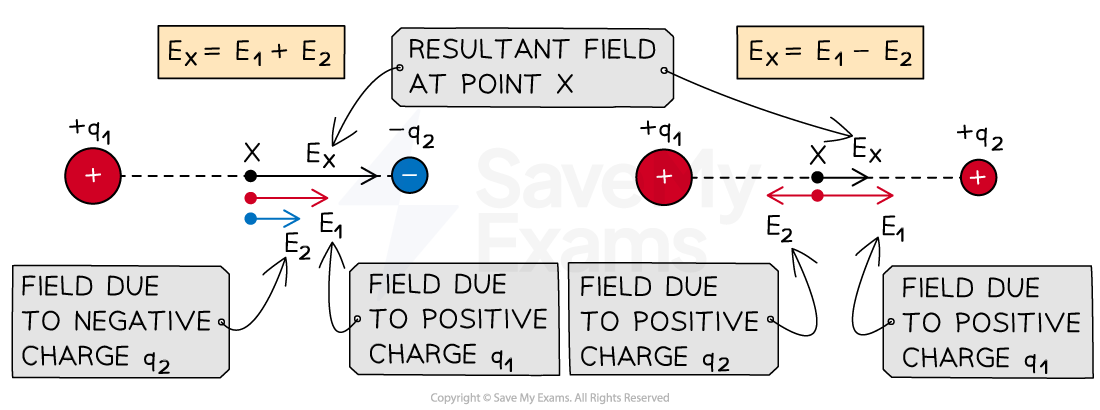
vector-addition-of-electric-field-strength

For charges along the same line, the resultant field is the vector addition of the field due to both charges at a particular point

  • For a point on the same line as two charges q1 and q2, with field strengths E1 and E2 respectively, the magnitude of the resultant field will be:
    • The sum of the fields, E1 + E2, if they are both in the same direction
    • The difference between the fields, E1 − E2, if they are in opposite directions
  • The direction of the resultant field depends on:
    • The types of charge (positive or negative)
    • The magnitude of the charges
  • For a point which makes a right-angled triangle with the charges, the resultant field can be determined using Pythagoras theorem

Vector addition of electric field components

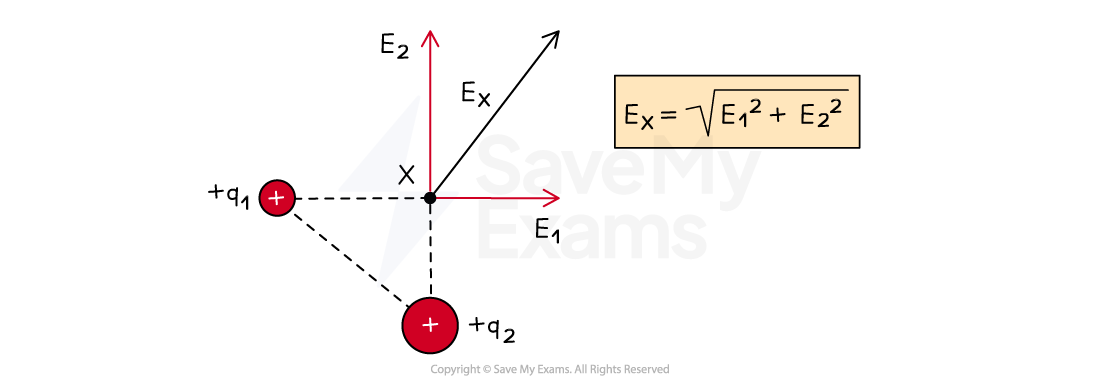
4-2-5-vector-addition-of-electric-field-strength-with-pythagoras

For charges which make a right-angle triangle with point X, the resultant field is the vector addition of the field due to both charges using Pythagoras theorem

Worked example

A metal sphere of diameter 15 cm is negatively charged. The electric field strength at the surface of the sphere is 1.5 × 105 V m−1.

Determine the total surface charge of the sphere.

Answer:

Step 1: List the known quantities

  • Electric field strength, E = 1.5 × 105 V m−1
  • Radius of sphere, r = 15 / 2 = 7.5 cm = 7.5 × 10−2 m
  • Permittivity of free space, ε0 = 8.85 × 10−12 F m−1

Step 2: Write down the equation for electric field strength

E space equals space fraction numerator Q over denominator 4 straight pi epsilon subscript 0 r squared end fraction

Step 3: Rearrange for charge Q

  • Recall that, for an external observer, a charged sphere can be considered as a point charge
  • The field strength at the surface of the sphere is equal to the field strength 15 cm away from a point charge with the same total charge as the sphere

Q space equals space 4 straight pi epsilon subscript 0 E r squared

Step 4: Substitute in the values and calculate:

Q = (4π × 8.85 × 10−12) × (1.5 × 105) × (7.5 × 10−2)2 = 9.38 × 10−8 C

  • The particle has a charge of 9.4 × 10−8 C or 94 nC

Examiner Tip

When combining electric fields from multiple charges, remember that the point (e.g. point X in the examples above) represents a positive test charge, so the direction of the electric force or field will correspond to the signs of the charges; the direction of the force or field points away from a positive charge and towards a negative charge.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Electric Force Between Two Point ChargesNext:Electric Potential
    Ann H

    Author: Ann H

    Expertise: Physics

    Ann obtained her Maths and Physics degree from the University of Bath before completing her PGCE in Science and Maths teaching. She spent ten years teaching Maths and Physics to wonderful students from all around the world whilst living in China, Ethiopia and Nepal. Now based in beautiful Devon she is thrilled to be creating awesome Physics resources to make Physics more accessible and understandable for all students no matter their schooling or background.