Electric Field Strength

When two points in an electric field are at different potentials, there is a potential difference between them
- To move a charge across that potential difference, work needs to be done on the charge
- Two charged parallel plates with a potential difference of V between them create a uniform electric field

The magnitude of the uniform electric field strength between two charged parallel plates is defined by the equation:

$E = \frac{∆ V}{∆ d}$

Where:
- E = electric field strength (V m⁻¹)
- ΔV = potential difference between the plates (V)
- Δd = distance between the plates (m)

Note: both units for electric field strength, V m⁻¹ and N C⁻¹, are equivalent
The equation shows:
- the greater the potential difference between the plates, the stronger the field
- the greater the separation between the plates, the weaker the field

This equation cannot be used to find the electric field strength around a point charge
- This is because the field around a point charge is radial

The electric field between two plates is directed:
- from the positive plate (i.e. the one connected to the positive terminal)
- to the negative plate (i.e. the one connected to the negative terminal)

Uniform electric field between two parallel plates

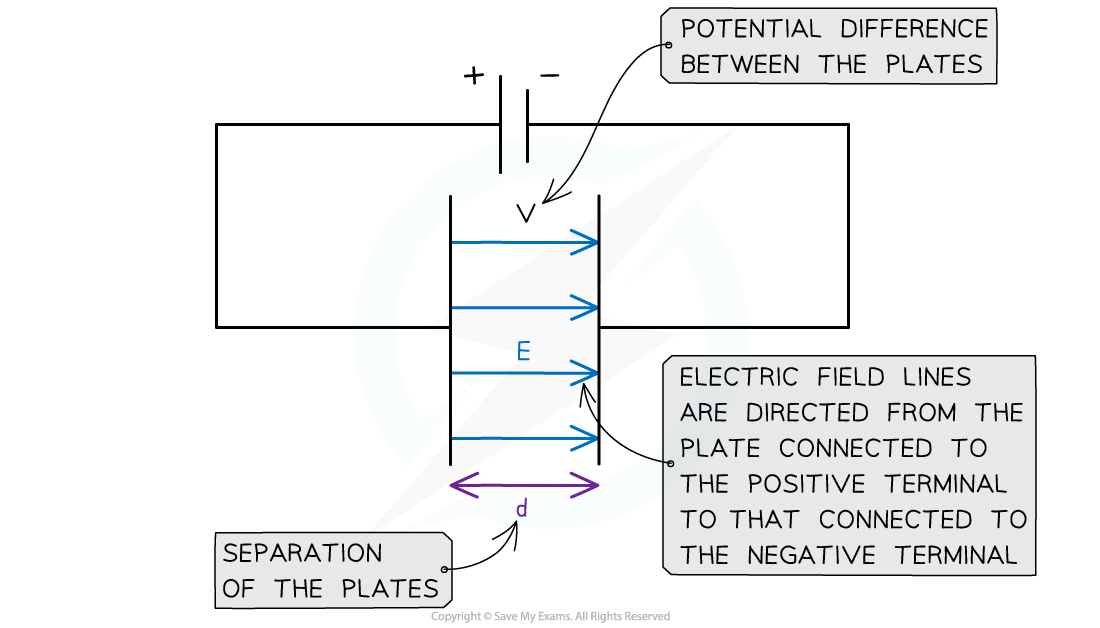
Electric field between two plates, downloadable AS & A Level Physics revision notes

The electric field strength between two charged parallel plates is the ratio of the potential difference and distance between the plates

Derivation of electric field strength between two parallel plates

When a charge q moves from one plate to the other, the work done on the charge by the field is

$W = F d$

Where:
- W = work done on charge (J)
- F = force on the charge (N)
- d = distance between plates (m)
The work done in moving a charge q through a potential difference V between parallel plates is given by:

$W = q V$

Equating the two expressions:

$F d = q V$

The electric field strength between the plates is therefore given by:

$E = \frac{F}{q} = \frac{V}{d}$

Parallel Plates Work Done, downloadable AS & A Level Physics revision notes

The work done on a charge in an electric field depends on the force and the distance between the plates

Worked example

Two parallel metal plates separated by 3.5 cm have a potential difference of 7.9 kV between them.

Calculate the electric force acting on a stationary point charge of 2.6 × 10⁻¹⁵ C when placed between the plates.

Answer:

Step 1: List the known quantities

Potential difference between plates, V = 7.9 kV = 7900 V
Distance between plates, d = 3.5 cm = 0.035 m
Charge, q = 2.6 × 10⁻¹⁵ C

Step 2: Equate the equations for electric field strength

E field between parallel plates: $E = \frac{V}{d}$

E field on a point charge: $E = \frac{F}{q}$

$E = \frac{F}{q} = \frac{V}{d}$

Step 3: Rearrange the expression for electric force F

$F = \frac{q V}{d}$

Step 4: Substitute values to calculate the force on the point charge

$F = \frac{(2.6 \times 10^{- 15}) \times 7900}{0.035} = 5.9 \times 10^{- 10}$ N (2 s.f.)

Examiner Tip

Remember the equation for electric field strength with V and d is only valid for parallel plates, and not for point charges

However, when a point charge moves between two parallel plates, the two equations for electric field strength can be equated:

$E = \frac{F}{Q} = \frac{V}{d}$

Top tip: if one of the parallel plates is earthed, it has a voltage of 0 V

Electric Field Strength (CIE A Level Physics)

Revision Note