Energy in SHM (Cambridge (CIE) A Level Physics)

Kinetic & potential energies

• Simple harmonic motion also involves an interchange between potential and kinetic energy

  • The swinging of a pendulum is an interplay between gravitational potential energy and kinetic energy

  • The horizontal oscillation of a mass on a spring is an interplay between elastic potential energy and kinetic energy

  • The vertical oscillation of a mass on a spring is an interplay between elastic potential energy, gravitational potential energy and kinetic energy

Energy of a horizontal mass-spring system

• The system has the maximum amount of elastic potential energy when the spring is stretched or compressed to its maximum displacement from the equilibrium position (amplitude)

• When the mass is released, it moves towards the equilibrium position, accelerating as it goes, causing the kinetic energy to increase

• At the equilibrium position, the velocity of the mass is at its maximum, therefore the kinetic energy is at its maximum and elastic potential energy is at its minimum

• Once past the equilibrium position the kinetic energy decreases and elastic potential energy increases 

Energy interchange for horizontal mass-spring system

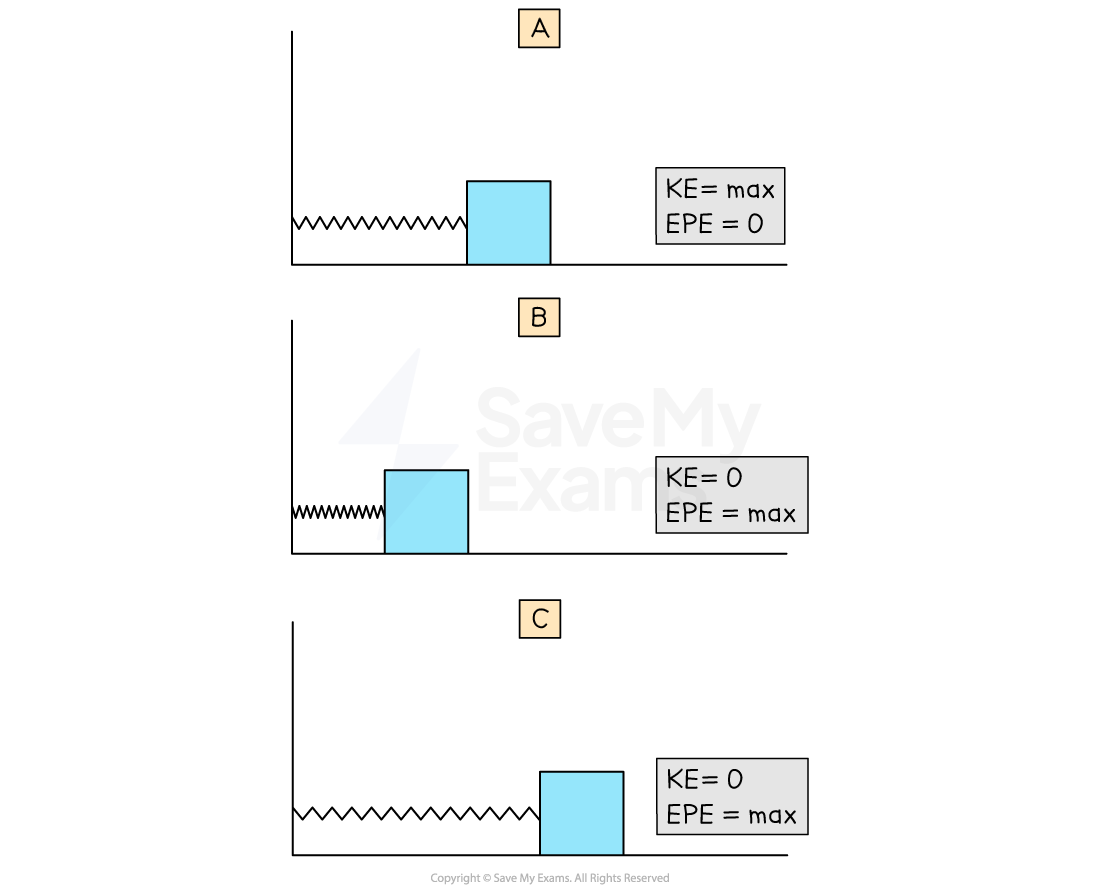
In a horizontal mass-spring system the kinetic energy is maximum in the equilibrium position and the elastic potential energy is maximum in the amplitude position

Energy of a simple pendulum

• The pendulum has its maximum gravitational potential energy at the point of maximum displacement from the equilibrium position (amplitude)

• When the pendulum is released, it moves towards the equilibrium position, accelerating as it goes and the kinetic energy increases

• As the pendulum swings through the equilibrium position, its velocity is at a maximum, and therefore kinetic energy is at a maximum and gravitational potential energy is at a minimum

• Once the mass has passed the equilibrium position, kinetic energy decreases and gravitational potential energy increases

Energy interchange for a simple pendulum

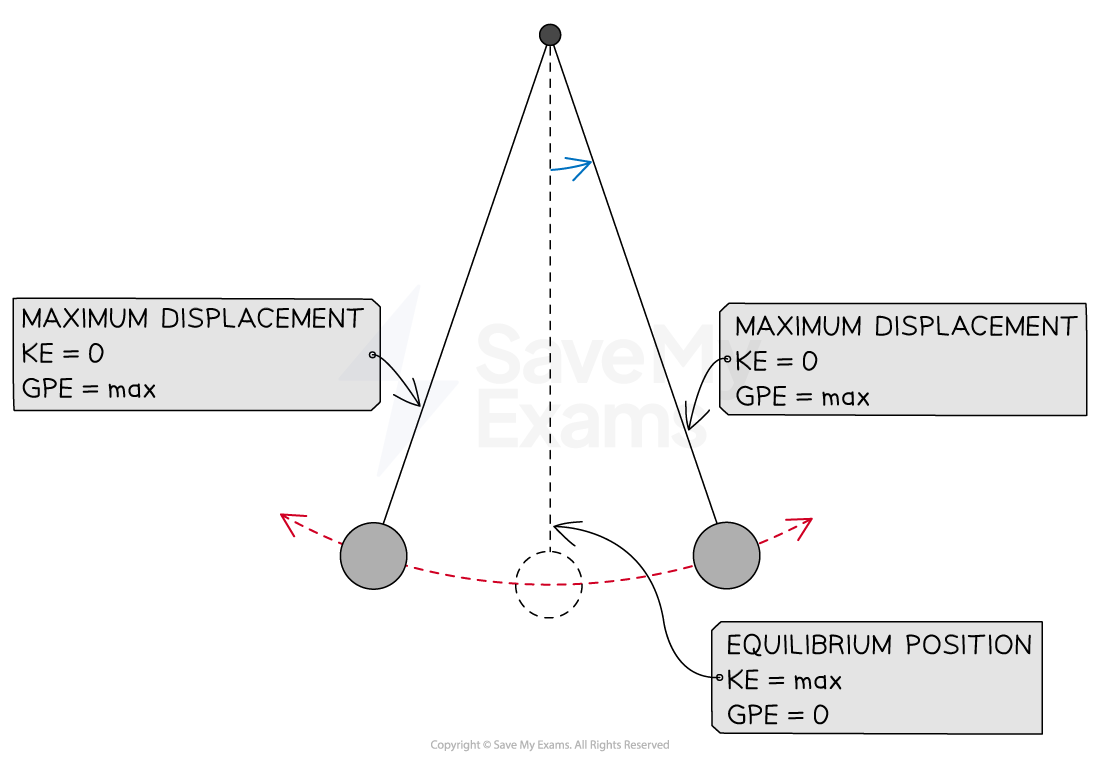
In a simple pendulum, the kinetic energy is maximum in the equilibrium position and the gravitational potential energy is maximum in the amplitude position

Calculating total energy of a simple harmonic system

Total energy equation

• The total energy of a system undergoing simple harmonic motion is defined by:

• Where:

  • E = total energy of a simple harmonic system (J)

  • m = mass of the oscillator (kg)

  • ⍵ = angular frequency (rad s^-1)

  • x₀ = amplitude (m)

Sum of potential and kinetic energies

• The total energy in the system remains constant, but the amount of kinetic and potential energy varies throughout the oscillation

• Total energy is the sum of the potential and kinetic energies:

E = E_P + E_K

• Where:

  • E = total energy in joules (J)

  • E_P = potential energy in joules (J)

  • E_K = kinetic energy in joules (J)

• Remember the equations for potential and kinetic energy:

  • Gravitational potential energy: E_p = mgh

  • Elastic potential energy, E_p = 

  • Kinetic energy, E_k = 

Energy-displacement graph

• The kinetic and potential energy transfers go through two complete cycles during one period of oscillation

  • One complete oscillation reaches the maximum displacement twice (once on the positive side and once on the negative side of the equilibrium position)

• You need to be familiar with the graph showing the total, potential and kinetic energy transfers in half an SHM oscillation (half a cycle)

Energy displacement graph for half an oscillation

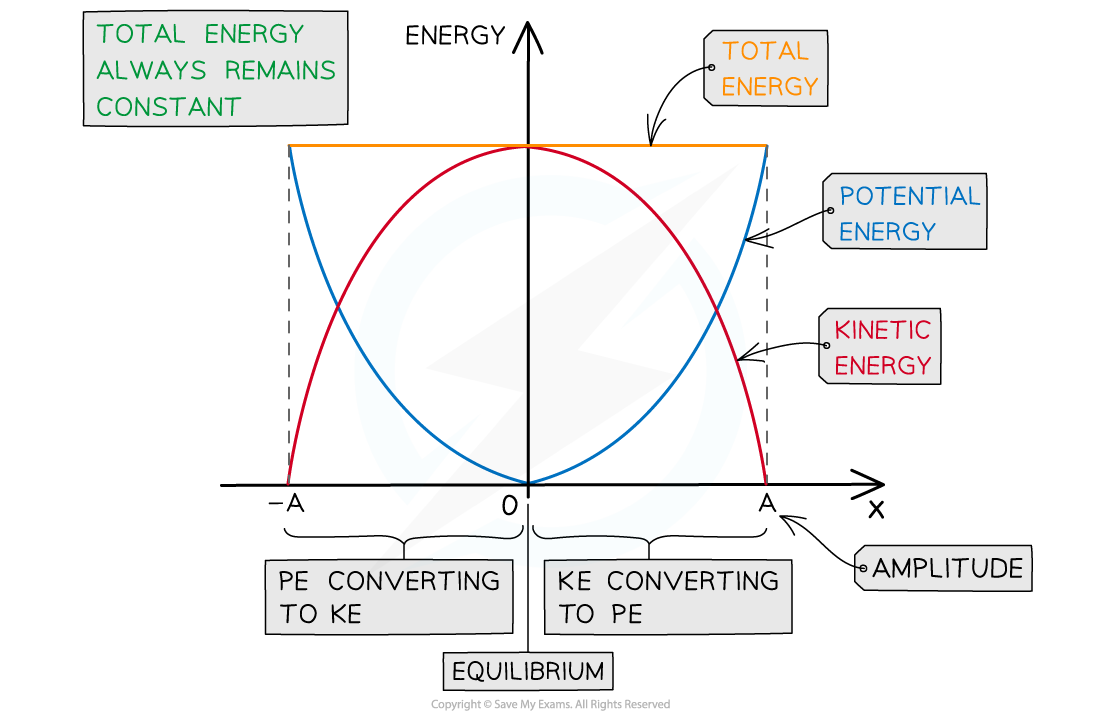
Graph showing the potential and kinetic energy against displacement in half a period of an SHM oscillation

• The key features of the energy-displacement graph are:

  • Displacement occurs in both directions, so the graph has both positive and negative x values

  • The potential energy is always maximum at the amplitude positions x = A

  • The potential energy is always at a minimum or zero at the equilibrium position x = 0

    • This is represented by a ‘U’ shaped curve

  • The kinetic energy is the opposite: 

  • Kinetic energy is at a minimum or zero at the amplitude positions x = A

  • Kinetic energy is at a maximum at the equilibrium position x = 0

    • This is represented by an ‘n’ shaped curve

  • The total energy is represented by a horizontal straight line above the curves