Syllabus Edition

First teaching 2023

First exams 2025

Gravitational Potential (CIE A Level Physics)

Revision Note

Test yourself

Author

Leander

Last updated

30 October 2024

Gravitational potential

Gravitational potential, φ, at a point is defined as:

The work done per unit mass in bringing a small test mass from infinity to the point

Gravitational potential always has a negative value because:
- It is defined as having a value of zero at infinity
- Since the gravitational force is attractive, work must be done on a mass to reach infinity

On the surface of a mass (such as a planet), gravitational potential also has a negative value
- The value becomes less negative, i.e. it increases, with distance from that mass

Work has to be done against the gravitational pull of the planet to take a unit mass away from the planet
The gravitational potential at a point depends on:
- The mass of the object
- The distance from the centre of mass of the object to the point

Changing gravitational potential

Gravitational Potential

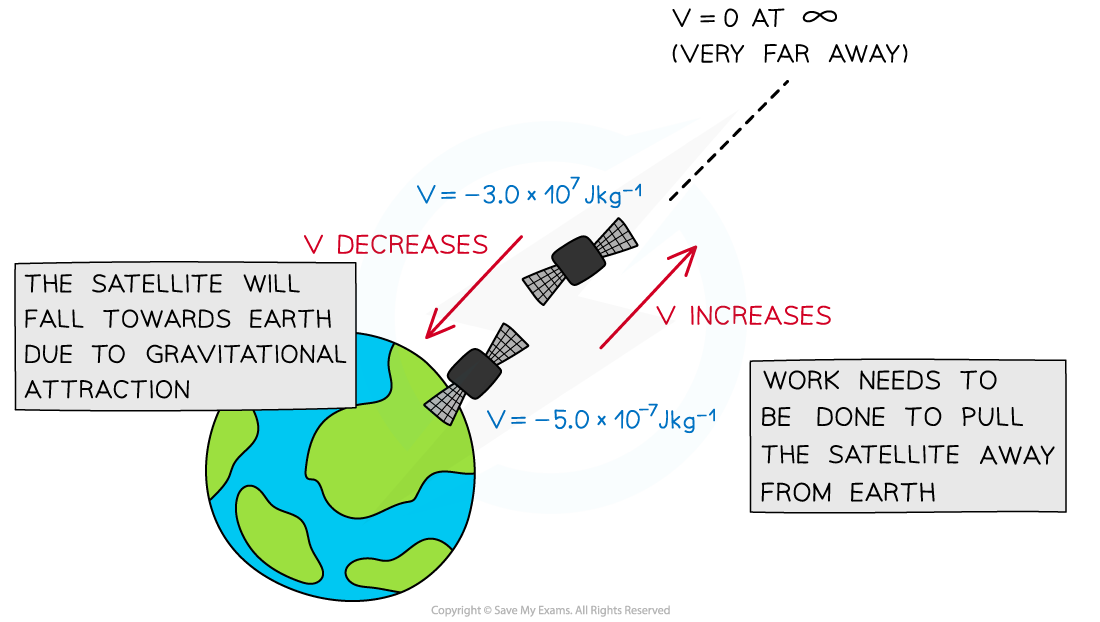
Gravitational potential decreases as the satellite moves closer to the Earth

Calculating gravitational potential

The gravitational potential, φ, in a field due to a point mass, M is given by the equation:

$φ = - \frac{G M}{r}$

Where:
- φ = gravitational potential (J kg^-1)
- G = Newton’s gravitational constant
- M = mass of the body producing the gravitational field (kg)
- r = distance from the centre of the mass to the point mass (m)

Change in gravitational potential

Two points at different distances from a mass will have different gravitational potentials
- This is because the gravitational potential increases with distance from a mass
Therefore, there will be a gravitational potential difference Δφ between the two points

$∆ φ = φ_{f} - φ_{i}$

Where:
- $φ_{i}$ = initial gravitational potential (J kg^–1)
- $φ_{f}$ = final gravitational potential (J kg^–1)

The change in gravitation potential Δφ is calculated using the equation:

$∆ φ = - \frac{G M}{r_{2}} - (- \frac{G M}{r_{1}})$

Where:
- r₁ = initial distance from the centre of mass to the point mass (m)
- r₂ = final distance from the centre of mass to the point mass (m)

Worked example

A planet has a diameter of 7600 km and a mass of 3.5 × 10²³ kg. A rock of mass 528 kg accelerates towards the planet from infinity.

At a distance of 400 km above the planet’s surface, calculate the gravitational potential of the rock.

Answer:

Step 1: Write the gravitational potential equation

$ϕ = - \frac{G M}{r}$

Step 2: Determine the value of r

r is the distance from the centre of the planet
Radius of the planet = planet diameter ÷ 2 = 7600 ÷ 2 = 3800 km

r = 3800 + 400 = 4200 km = 4.2 × 10⁶ m

Step 3: Substitute in values

$ϕ = - \frac{(6.67 \times 10^{- 11}) \times (3.5 \times 10^{23})}{4.2 \times 10^{6}} = - 5.6 \times 10^{6} J {kg}^{- 1}$

Examiner Tip

Remember to keep the negative sign in your solution for gravitational potential. However, if you’re asked for the ‘change in’ gravitational potential, no negative sign should be included since you are finding a difference in values (between 0 at infinity and the gravitational potential from your calculation).

Gravitational potential energy between two point masses

Gravitational potential energy

In a Radial field, gravitational potential energy (GPE) describes the energy an object possesses due to its position in a gravitational field

The gravitational potential energy of a system is defined as:

The work done to assemble the system from infinite separation of the components of the system

The equation for GPE between two point masses m₁ and m₂ at a distance r is:

$E_{p} = - \frac{G m_{1} m_{2}}{r}$

Where:
- G = universal gravitational constant (N m² kg^–²)
- m₁ = larger mass producing the field (kg)
- m₂ = mass moving within the field of m₁ (kg)
- r = distance between the centre of m₁ and m₂ (m)

Gravitational potential energy vs distance

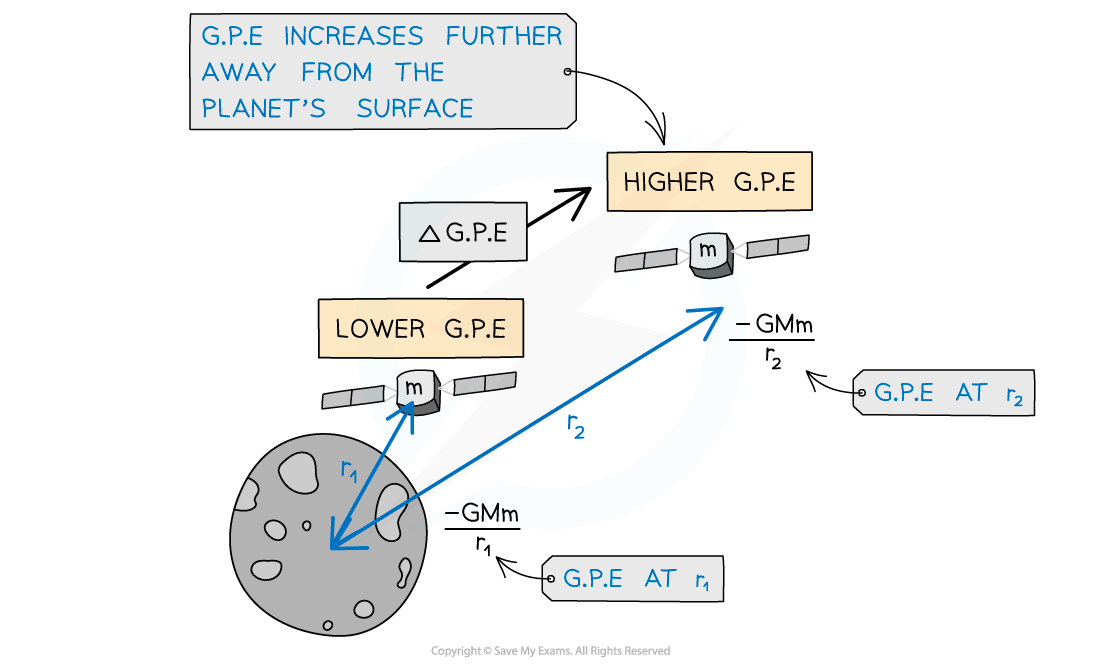
Change in GPE, downloadable AS & A Level Physics revision notes

Gravitational potential energy increases as a satellite leaves the surface of the Moon (of mass M)

Change in gravitational potential energy

The change in GPE when a small mass, m₂ moves towards, or away from, another larger mass, m₁ is given by:

$∆ E_{p} = - \frac{G m_{1} m_{2}}{r_{2}} - (- \frac{G m_{1} m_{2}}{r_{1}})$

$∆ E_{p} = G m_{1} m_{2} (\frac{1}{r_{1}} - \frac{1}{r_{2}})$

Where:
- m₁ = mass that is producing the gravitational field (e.g. a planet) (kg)
- m₂ = mass that is moving in the gravitational field (e.g. a satellite) (kg)
- r₁ = first distance of m₂ from the centre of m₁(m)
- r₂ = second distance of m₂ from the centre of m₁ (m)

Work done

The Work done against a gravitational field is equal to the change in gravitational potential energy (GPE) of an object in a gravitational field
- For example, a satellite lifted into space from the Earth’s surface

Recall that work done is equal to:
- force applied multiplied by the displacement of the object
- energy transferred

$work done = force \times displacement$

Recall that Newton's Law of Gravitation relates the magnitude of the gravitational force F between two masses m₁ and m₂ separated by distance r is:

$F = \frac{G m_{1} m_{2}}{r^{2}}$

So the work done by the gravitational force is equivalent to the change in gravitational potential energy:

$Work done = ∆ E_{p} = G m_{1} m_{2} (\frac{1}{{(r_{1} - r_{2})}^{2}}) \times (r_{1} - r_{2})$

$∆ E_{p} = G m_{1} m_{2} (\frac{1}{(r_{1} - r_{2})})$

Examiner Tip

Make sure to not confuse the ΔG.P.E equation with

ΔG.P.E = mgΔh

The above equation is only relevant for an object lifted in a uniform gravitational field (close to the Earth’s surface). The new equation for G.P.E will not include g, because this varies for different planets and is no longer a constant (decreases by 1/r²) outside the surface of a planet.

Remember, multiplying two negative numbers equals a positive number, for example:

$- (- \frac{G M}{r}) = + \frac{G M}{r}$

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: