Gravitational Force Between Point Masses (Cambridge (CIE) A Level Physics) : Revision Note
Newton's law of gravitation
The gravitational force between two bodies outside a uniform field, e.g. between the Earth and the Sun, is defined by Newton’s law of gravitation
Newton’s law of gravitation states that:
The gravitational force between two point masses is proportional to the product of the masses and inversely proportional to the square of their separation
In equation form, this can be written as:
Where:
FG = gravitational force between two masses (N)
G = Newton’s gravitational constant
m1 and m2 = two points masses (kg)
r = distance between the centre of the two masses (m)
Gravitational force between two point masses
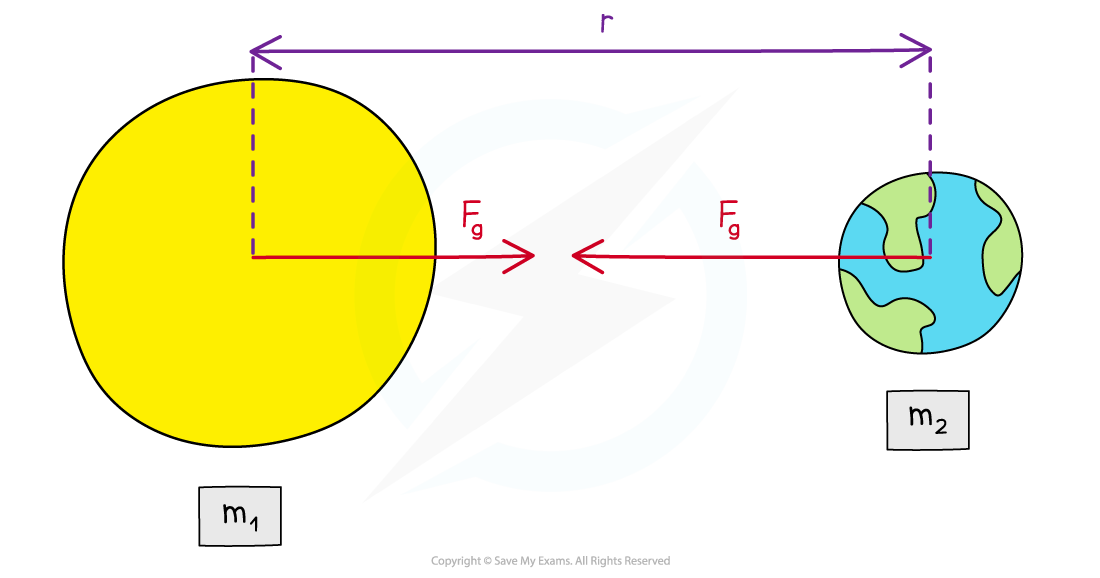
The gravitational force between two point masses outside a uniform field is defined by Newton’s law of gravitation
Newton’s law of gravitation applies to orbiting bodies, e.g. planets orbiting the Sun
Although stars and planets are very large, they can be considered to be point masses as:
they are approximately uniform spheres
their separation is much larger than their radii
The
relation is called the inverse square law
This means that when a mass is twice as far away from another, the gravitational force reduces by a quarter, i.e.
Worked Example
A satellite of mass 6500 kg is orbiting the Earth at 2000 km above the Earth's surface.
The gravitational force between them is 37 kN. The radius of the Earth is 6400 km.
Calculate the mass of the Earth.
Answer:
Step 1: List the known quantities
Mass of satellite, m1 = 6500 kg
m1 and m2 can be either way around
Distance of satellite above Earth's surface = 2000 km
Gravitational force, FG = 37 kN
Radius of Earth = 6400 km
Step 2: State the equation for Newton's Law of Gravitation and rearrange for the mass of the Earth
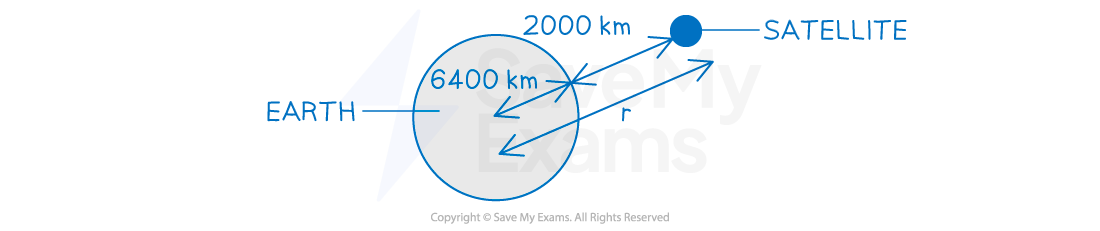
Step 3: Calculate the distance, r
r is the distance between the centre of the Earth and the satellite
r = distance of satellite above Earth's surface + radius of Earth
Step 4: Substitute the known values into Newton's Law of Gravitation to calculate the mass of the Earth
Examiner Tips and Tricks
A common mistake in exams is to forget to add together the distance from the surface of the planet and its radius to obtain the value of r. The distance r is measured from the centre of the mass, which is from the centre of the planet.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
