Circular Orbits in Gravitational Fields (Cambridge (CIE) A Level Physics): Revision Note

Circular orbits in gravitational fields

• The orbits of most planets and satellites in the Solar System are nearly circular

• The gravitational force between two bodies provides the centripetal force required to maintain a circular orbit

• Consider a satellite with mass m orbiting Earth with mass M at a distance r from the centre, travelling with linear speed v

• Equating the gravitational force to the centripetal force for a planet or satellite in orbit gives:

• The mass of the satellite m will cancel out on both sides to give:

• Where:

  • = orbital speed of the smaller mass (m s⁻¹)

  • G = Newton's Gravitational Constant

  • M = mass of the larger mass being orbited (kg)

  • r = orbital radius (m)

• This equation shows that all satellites moving in a circular orbit of fixed radius will travel at a constant speed

• The direction of a satellite orbiting in circular motion is constantly changing, which means that the satellite has

  • a velocity which is constantly changing

  • a centripetal acceleration that acts towards the satellite

  • a centripetal force, provided by the gravitational force, which causes the satellite to accelerate

Gravitational force and instantaneous velocity

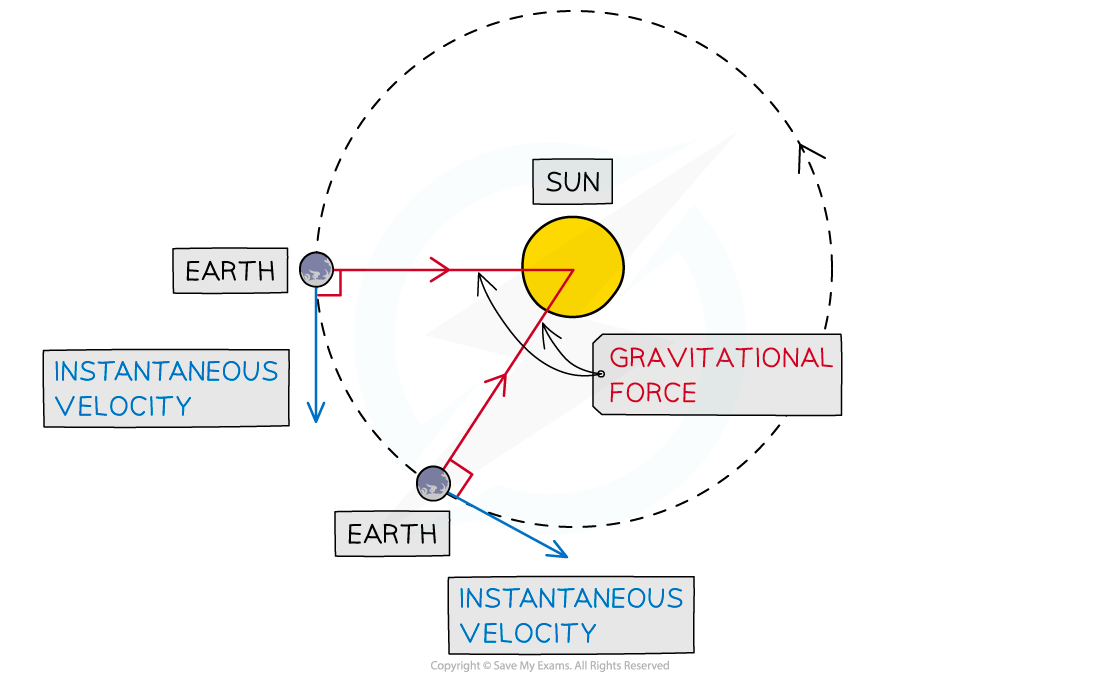
The direction of the instantaneous velocity and the gravitational force at different points of the Earth’s orbit around the sun