Gravitational Fields (Cambridge (CIE) A Level Physics)

Defining gravitational field

• There is a force of attraction between all masses

  • This force is known as the ‘force due to gravity’ or the weight

• The Earth’s gravitational field is responsible for the weight of all objects on Earth

• A gravitational field is an example of a field of force and is defined as:

  Force per unit mass

• The direction of the gravitational field is always towards the centre of the mass

  • Gravitational forces cannot be repulsive

Gravitational field strength 

• The strength of this gravitational field (g) at a point is the force (F_g) per unit mass (m) of an object at that point:

• Where:

  • g = gravitational field strength (N kg^-1)

  • F_g = force due to gravity, or weight (N)

  • m = mass (kg)

• This equation tells us:

  • On planets with a large value of g, the gravitational force per unit mass is greater than on planets with a smaller value of g

  • This means objects will have a larger weight with a larger value of g

Weight of person on Earth and on Jupiter

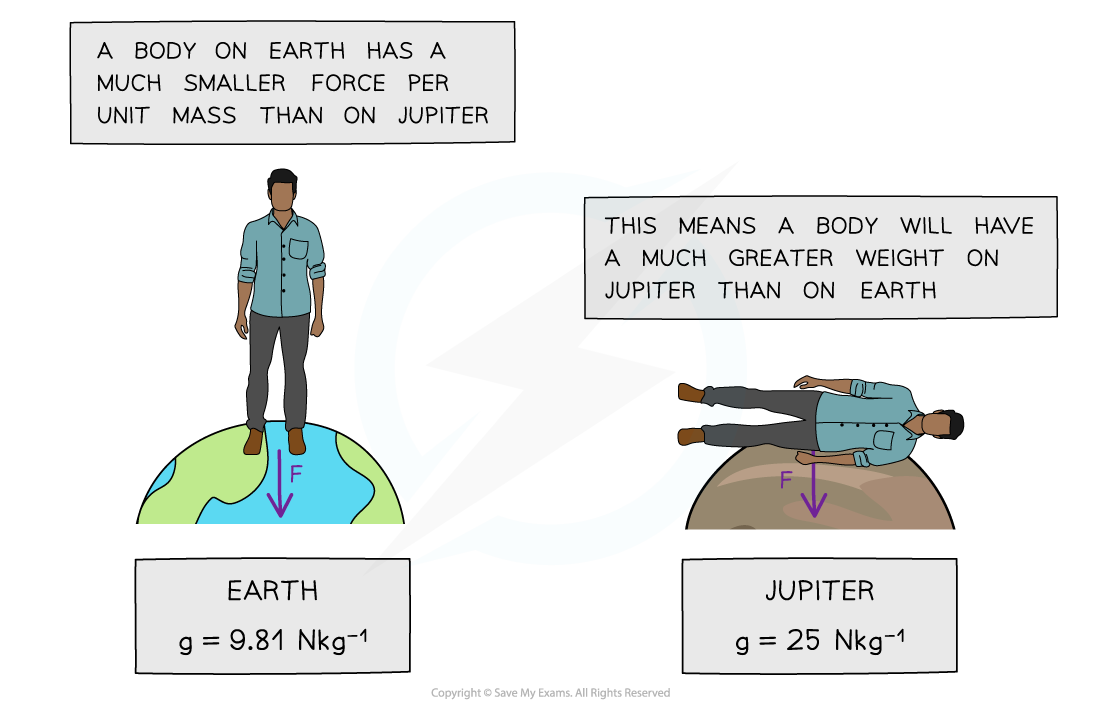
A person’s weight on Jupiter would be so large a human would be unable to fully stand up

Representing gravitational fields

• The direction and magnitude of a gravitational field is represented by gravitational field lines

  • Gravitational fields can be uniform or non-uniform

• Radial fields are non-uniform fields

  • The gravitational field strength g decreases with distance from the centre of the object

  • The gravitational field lines around a point mass are directed radially inwards

• Parallel field lines represent a uniform field

  • The gravitational field strength g is the same throughout the field

  • The gravitational field lines of a uniform field, where the field strength is the same at all points, is represented by equally spaced parallel lines

  • The Earth's gravitational field near the surface is almost uniform; therefore, it can be approximated as uniform

Gravitational field lines for a point mass and for a uniform gravitational field

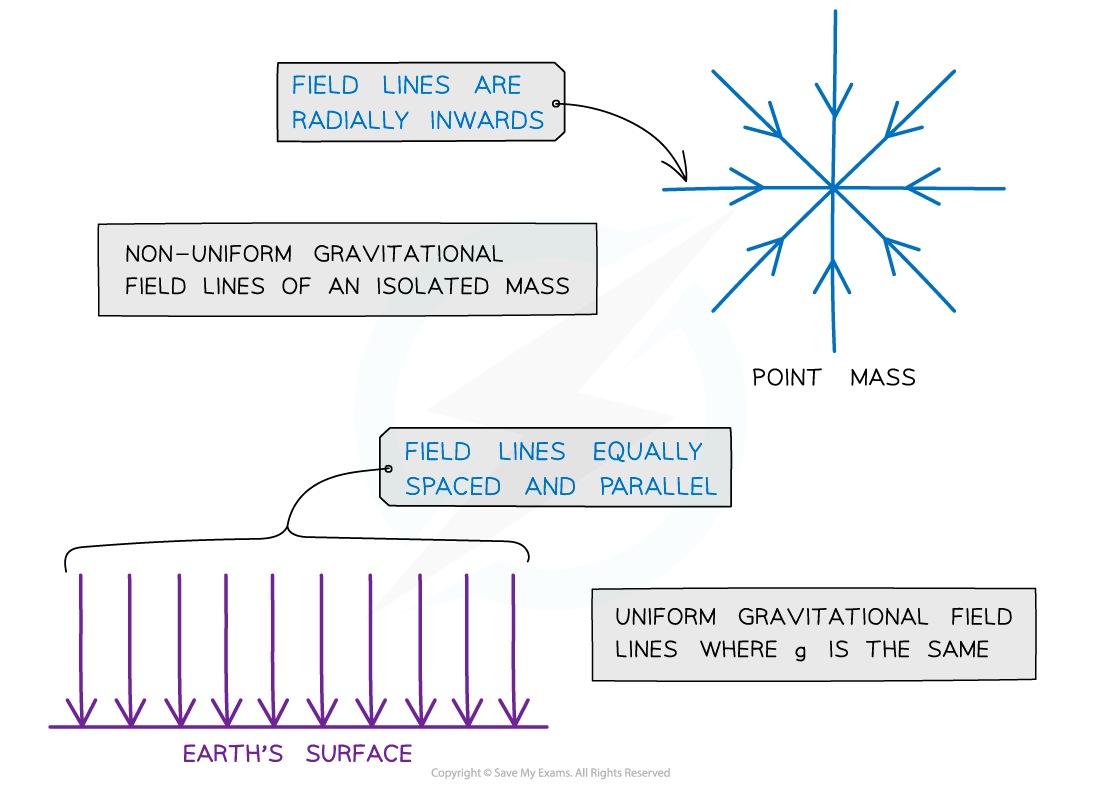
Gravitational field lines for a point mass are radial and, for a uniform gravitational field, are parallel