Calculating Centripetal Acceleration (CIE A Level Physics)

Revision Note

Test yourself

Author

Leander

Last updated

22 October 2024

Calculating centripetal acceleration

Centripetal acceleration is defined as:

The acceleration of an object towards the centre of a circle when an object is in motion (rotating) around a circle at a constant speed

It can be defined using the radius r and linear speed v:

$a = \frac{v^{2}}{r}$

Where:
- a = centripetal acceleration (m s^–2)
- v = linear speed (m s^–1)
- r = radius of the circular orbit (m)
Using the equation relating angular speed ω and linear speed v:

$v = r ω$

Where:
- ω = angular speed (rad s^–¹)

These equations can be combined to give another form of the centripetal acceleration equation:

$a = \frac{{(r ω)}^{2}}{r}$

$a = r ω^{2}$

Centripetal acceleration

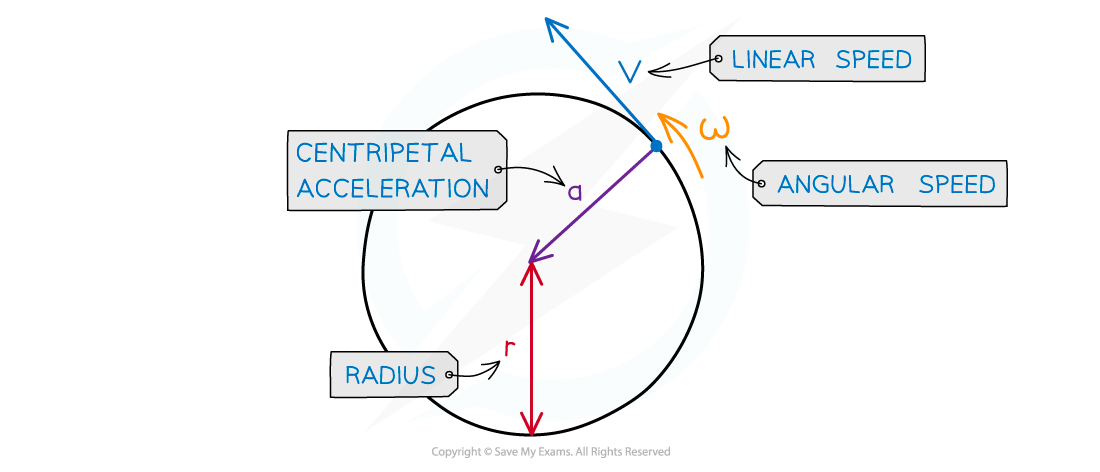
Centripetal acceleration diagram, downloadable AS & A Level Physics revision notes

Centripetal acceleration is always directed toward the centre of the circle, and is perpendicular to the object’s velocity

Where:
- a = centripetal acceleration (m s⁻²)
- v = linear speed (m s⁻¹)
- ⍵ = angular speed (rad s⁻¹)
- r = radius of the orbit (m)

Worked example

A ball tied to a string is rotating in a horizontal circle with a radius of 1.5 m and an angular speed of 3.5 rad s⁻¹.

Calculate its centripetal acceleration if the radius was twice as large and angular speed was twice as fast.

Answer:

Step 1: State acceleration in terms of angular speed

$a = r ω^{2}$

Step 2: Increase angular acceleration with twice the radius and twice the angular speed

$a = (2 r) \times {(2 ω)}^{2} = 2 r \times 4 ω^{2} = 8 r ω^{2}$

The centripetal acceleration will be 8× bigger

Step 3: Substitute in the known values to calculate

$a = 8 r ω^{2} = 8 \times 1.5 \times 3 . 5^{2} = 147 m s^{- 2}$

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?

Author: Leander

Expertise: Physics

Leander graduated with First-class honours in Science and Education from Sheffield Hallam University. She won the prestigious Lord Robert Winston Solomon Lipson Prize in recognition of her dedication to science and teaching excellence. After teaching and tutoring both science and maths students, Leander now brings this passion for helping young people reach their potential to her work at SME.