Syllabus Edition

First teaching 2023

First exams 2025

Alpha, Beta & Gamma Particles (CIE A Level Physics)

Revision Note

Test yourself

Author

Leander

Last updated

28 October 2024

Conservation of nucleon number & charge

Nuclear processes such as fission and fusion are represented using nuclear equations (similar to chemical reactions in chemistry)
The number of protons and neutrons in atom is known as its constituents
For example:

${}_{92}^{235}U + {}_{0}^{1}n \to {}_{38}^{90}{Sr} + {}_{54}^{144}{Xe} + 2 {}_{0}^{1}n$

The above equation represents a fission reaction in which a uranium nucleus is hit with a neutron and splits into two smaller nuclei – a Strontium nucleus and Xenon nucleus, releasing two neutrons in the process
In nuclear equations, the nucleon number and charge are always conserved
This means that:
- the sum of the nucleons on the left hand side must equal the sum of the nucleons on the right hand side
- the sum of the charge on the left hand side must equal the sum of the charge on the right hand side
In the above equation, the sum of the nucleon (top) numbers on both sides are equal

$235 + 1 = 90 + 144 + (2 \times 1)$

$236 = 236$

The same is true for the proton (bottom) numbers

$92 + 0 = 38 + 54 + (2 \times 0)$

$92 = 92$

By balancing equations in this way, you can determine the nucleon number, proton number or the number of missing elements

Let's consider another example:

${}_{92}^{235}U + {}_{0}^{1}n \to {}_{37}^{96}{Rb} + {}_{55}^{137}{Cs} + N {}_{0}^{1}n$

Determine the total nucleon number
- This is determined from the side of the equation where all the values are known
- In this example, from the reactants

${}_{92}^{235}U + {}_{0}^{1}n$

- The total nucleon number = 235 + 1 = 236
Equate the total nucleon number to the total nucleon number of the products including the unknown N

${}_{37}^{96}{Rb} + {}_{55}^{137}{Cs} + N {}_{0}^{1}n$

- Total nucleon number of reactants = 96 + 137 + (N ×1) = 236
Rearrange to solve for N

$N = \frac{236 - 96 - 137}{1}$

$N = 3$

Balancing the equation shows that 3 neutrons must be released in the reaction

Worked example

When a californium atom reacts with an unknown element X, the following reaction occurs.

${}_{98}^{252}{Cf} + {}_{Y}^{10}X \to 3 {}_{0}^{1}n + {}_{103}^{Z}{Lr}$

Determine the missing values of Y and Z.

Answer:

Step 1: Identify what the value of Y represents

Y is the proton number of element X

Step 2: Determine the value of Y

Determine the number of protons on both sides of the equation

$98 + Y = (3 \times 0) + 103$

$Y = 0 + 103 - 98$

$Y = 5$

Step 3: Identify what the value of Z represents

Z is the nucleon number of the element Lr

Step 4: Determine the value of Z

Determine the total nucleon numbers on both sides of the equation

$252 + 10 = (3 \times 1) + Z$

$Z = 252 + 10 - 3$

$Z = 259$

Alpha, beta & gamma particles

Some elements have nuclei that are unstable
- This tends to be when the number of nucleons does not balance

In order to become more stable, they emit particles and/or electromagnetic radiation
- These nuclei are said to be radioactive

There are three main types of radioactive emission: alpha, beta and gamma

Alpha particles

Alpha (α) particles are high energy particles made up of 2 protons and 2 neutrons (the same as a helium nucleus)
They are usually emitted from nuclei that are too large

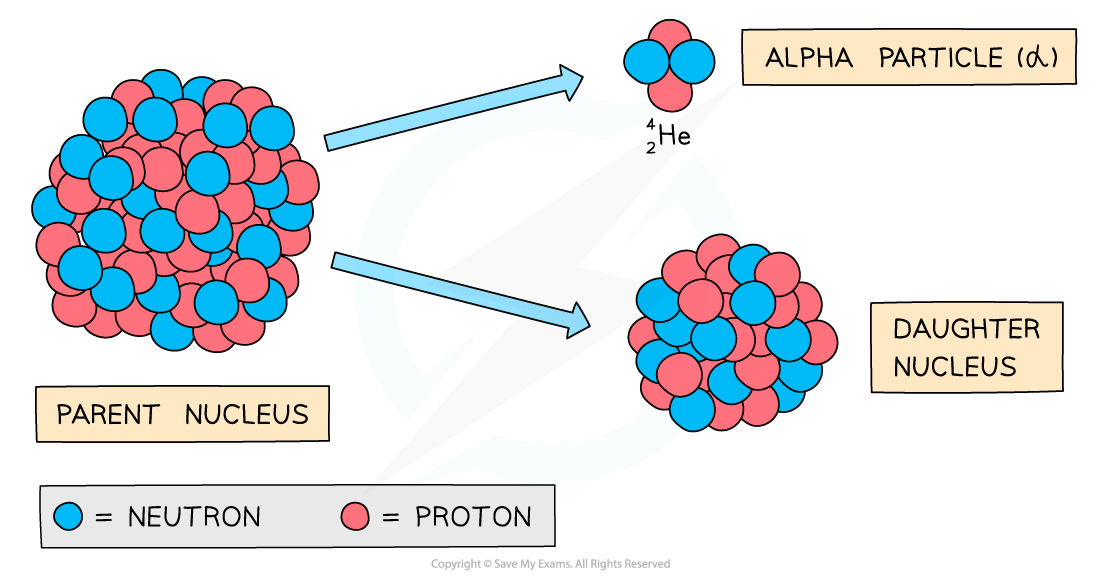
Alpha decay diagram, downloadable AS & A Level Physics revision notes

During alpha decay, a parent nucleus becomes a daughter nucleus by emitting an alpha particle (helium nucleus)

The nuclide notion for an alpha particle is:

${}_{2}^{4}α$ or ${}_{2}^{4}{He}$

Alpha is a highly ionising form of radiation
- It has a large charge of +2e
Alpha is a weakly penetrating form of radiation
- This is because it is so ionising, it readily interacts with any object instead of passing through it
- Alpha particles have a range of a few cm in air
Alpha particles can be blocked by skin or a piece of paper

Beta particles

Beta (β⁻) particles are high energy electrons emitted from the nucleus
- β⁻ particles are emitted by nuclei that have too many neutrons

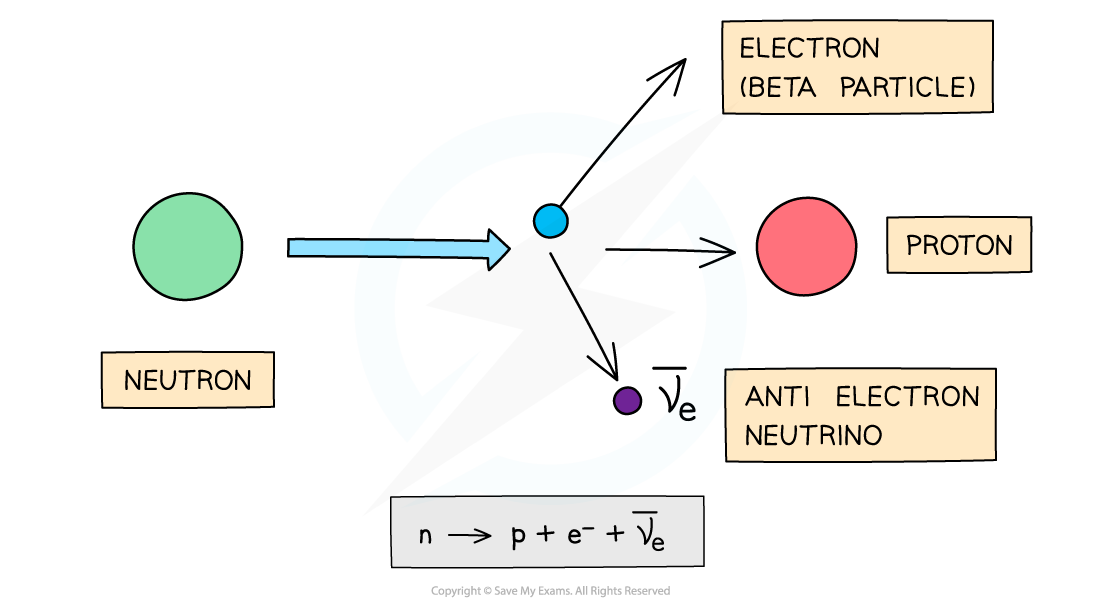
Beta minus decay diagram, downloadable AS & A Level Physics revision notes

During beta-minus decay, a neutron in a parent nucleus becomes a proton in a daughter nucleus by emitting a beta-minus particle (an electron) and an anti-electron neutrino

The nuclide notion for a beta minus particle is:

${}_{- 1}^{0}β$

Beta (β⁺) particles are high energy positrons emitted from the nucleus
- β⁺ particles are emitted by nuclei that have too many protons

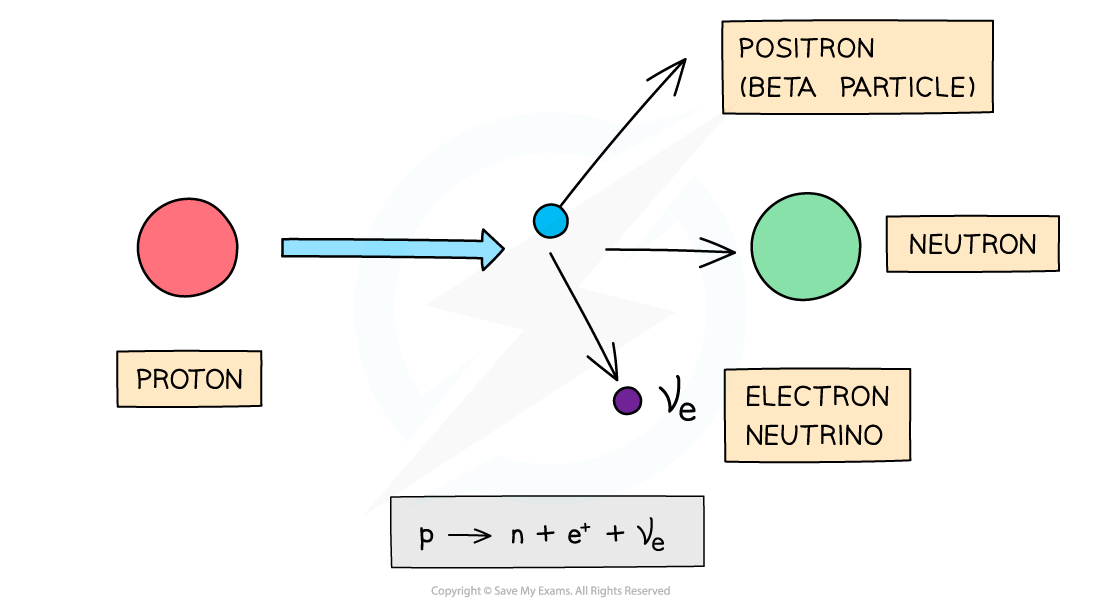
During beta-plus decay, a proton in a parent nucleus becomes a neutron in a daughter nucleus by emitting a beta-plus particle (a positron) and an electron neutrino

The nuclide notion for a beta plus particle is:

${}_{+ 1}^{0}β$

Beta is a moderately ionising type of radiation
- This is due to it having a charge of ±1e
- This means it is able to do some slight damage to cells (less than alpha but more than gamma)
Beta is a moderately penetrating type of radiation
- Beta particles have a range of around 20 cm - 3 m in air, depending on their energy
Beta particles can be stopped by a few millimetres of aluminium foil

Gamma rays

Gamma (γ) rays are high energy electromagnetic waves
They are emitted by nuclei that need to lose some energy

The nuclide notation for a gamma particle is:

${}_{0}^{0}γ$

If these particles hit other atoms, they can knock out electrons, ionising the atom
This can cause chemical changes in materials and can damage or kill living cells

Ionisation by radiation

Ionisation, downloadable AS & A Level Physics revision notes

When radiation passes close to atoms, it can knock out electrons, ionising the atom

The properties of the different types of radiation are summarised in the table below

Properties of types of radiation

Particle	Composition	Mass / u	Charge / e	Speed / c
Alpha (α)	2 protons + 2 neutrons	4	+2	0.05
Beta minus (β⁻)	Electron (e⁻)	0.0005	−1	>0.99
Beta plus (β⁺)	Positron (e⁺)	0.0005	+1	>0.99
Gamma (γ)	Electromagnetic wave	0	0	1

u is the atomic mass unit (see “Atomic Mass Unit (u)”)
e is the charge of the electron: 1.60 × 10^-19 C
c is the speed of light: 3 × 10⁸ m s^-1

Worked example

Three successive radioactive decays are shown in the diagram below. Each one results in a particle being emitted.

The first decay results in the emission of a β-particle.

The second decay results in the emission of an α-particle.

The third decay results in the emission of another β-particle.

11-1-4-we-alpha-beta-gamma-particles---cie-new

Nuclides W and Z are compared.

Which nuclide of Z is formed at the end of this decay?

A. ${}_{90}^{237}Z$ B: ${}_{92}^{233}Z$ C: ${}_{89}^{237}Z$ D: ${}_{90}^{233}Z$

Answer: D

Step 1: Write the equation for the β− decay

A β− particle is an electron
The nucleon number stays the same
The proton number increases by 1

${}_{92}^{237}W \to {}_{93}^{237}X + {}_{1}^{0}β$

Step 2: Write the equation for the α decay

An α particle is a helium nucleus
The nucleon number reduces by 4
The proton number reduces by 2

${}_{93}^{237}X \to {}_{91}^{233}Y + {}_{2}^{4}α$

Step 3: Write the equation for the β+ decay

A β+ particle is a positron
The nucleon number stays the same
The proton number reduces by 1

${}_{91}^{233}Y \to {}_{90}^{233}Z + {}_{+ 1}^{0}β$

Step 4: Determine the final nucleon Z

The final nucleon, Z will be:

${}_{90}^{233}Z$

Examiner Tip

It is important to be familiar the properties of each type of radiation and their symbols.

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?