State the physical quantity defined as the energy possessed by an object due to its position in a gravitational field.
Define gravitational potential at a point.
Gravitational potential, φ, is also defined by the equation
Fig. 1.1 shows a person on the surface of the Earth, a ball falling towards the centre of the Earth and a satellite in orbit around the Earth.
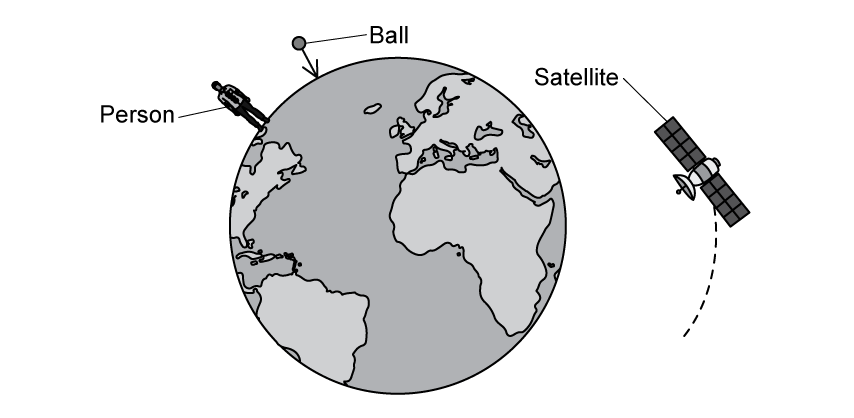
Identify the object which experiences the largest gravitational potential.
Did this page help you?




 Fig. 1.1
Fig. 1.1