Revision NotesExam QuestionsPast Papers
A LevelPhysicsCambridge (CIE)Revision Notes7. WavesProgressive WavesWave Intensity

Syllabus Edition

First teaching 2023

First exams 2025

|

Wave Intensity (Cambridge (CIE) A Level Physics)

Revision Note

Katie M

Written by: Katie M

Reviewed by: Caroline Carroll

Updated on

Wave intensity

  • Progressive waves transfer energy

  • The amount of energy passing through a unit area per unit time is the intensity of the wave

  • Therefore, the intensity is defined as power per unit area

I space equals space P over A

  • Where

    • I is intensity in W m−2

    • P is power in W

    • A is area in m2

  • The area the wave passes through is perpendicular to the direction of its velocity

  • The intensity of a progressive wave is also proportional to its amplitude squared and frequency squared

I space proportional to space A squared

I space proportional to space f squared

  • Where

    • A is amplitude in m

    • f is frequency in Hz

  •  Recall that ∝ means "proportional to"

  • This means that if the frequency or the amplitude is doubled, the intensity increases by a factor of 4 (22)

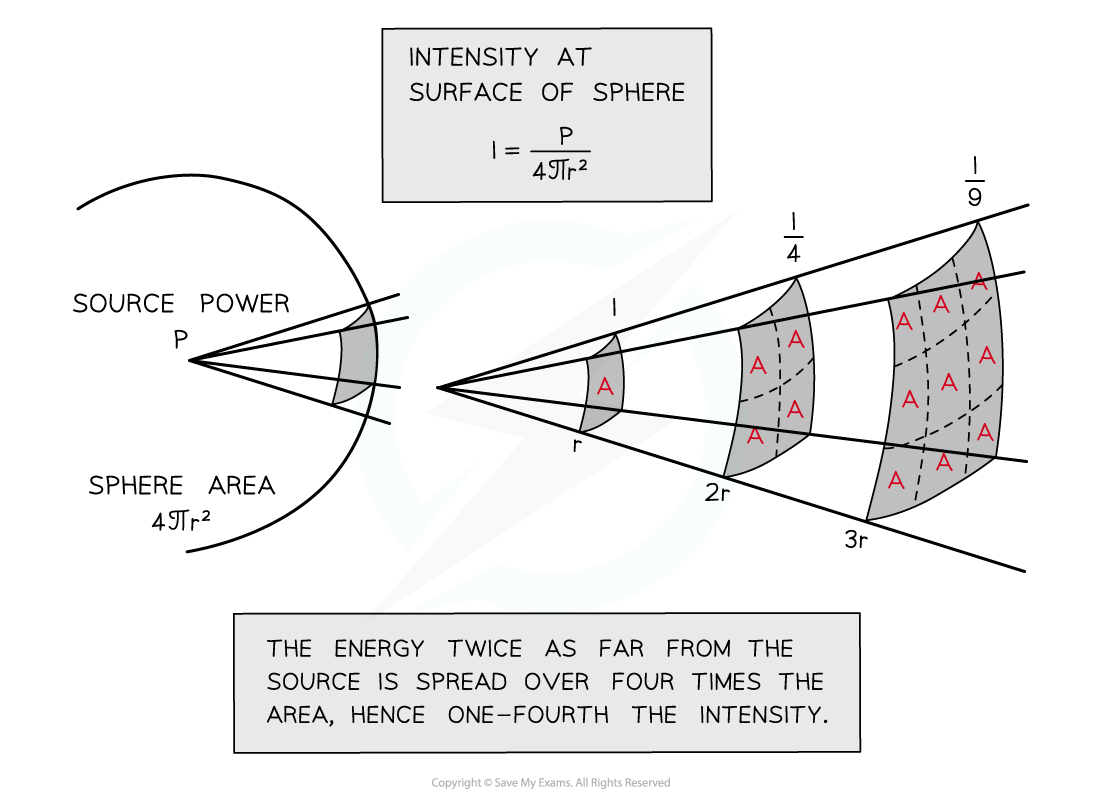
Spherical waves

  • A spherical wave is a wave from a point source which spreads out equally in all directions

  • The area the wave passes through is the surface area of a sphere: 4πr2

  • As the wave travels further from the source, the energy it carries passes through increasingly larger areas as shown in the diagram below:

Inverse square law for intensity

Intensity of a spherical wave, downloadable AS & A Level Physics revision notes

Intensity is proportional to the amplitude squared

 

  • Assuming none of the wave energy is absorbed, the intensity I decreases with increasing distance from the source

  • The inverse square law states that

     I space proportional to 1 over r squared

    • The inverse square law means when the source is twice as far away, the intensity is 4 times smaller

Worked Example

The intensity of a progressive wave is proportional to the square of the amplitude of the wave. It is also proportional to the square of the frequency. The variation with time t of displacement x of particles when two progressive waves Q and P pass separately through a medium, are shown on the graphs.

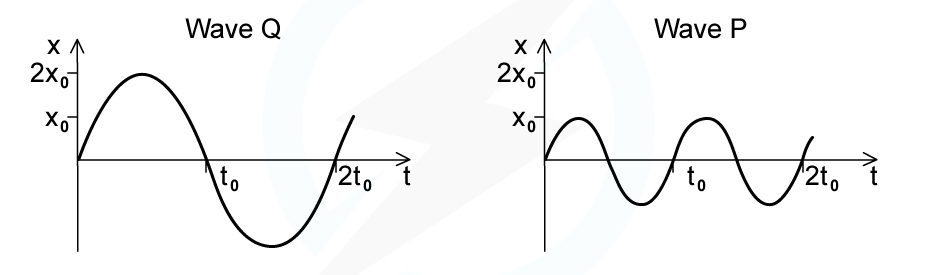
The intensity of wave Q is I0.What is the intensity of wave P?

Answer:

Step 1: Compare waves Q and P:

  • The amplitude of wave Q is twice the amplitude of wave P

  • The frequency of wave P is double the frequency of wave Q

Step 2: Evaluate how amplitude affects the intensities:

  • Q has twice the amplitude of P 

A subscript Q over A subscript P space equals space 2

  • The ratio of amplitudes squared is equal to the ratio of intensities, because intensity and amplitude squared are proportional

A subscript Q squared over A subscript P squared space equals space 4 space equals space I subscript Q over I subscript P

I subscript Q space equals space 4 I subscript P

  • So Q's larger amplitude increases its intensity by a factor of 4

Step 3: Evaluate how frequency affects the intensities:

  • Q has half the frequency of P

f subscript Q over f subscript P space equals space 1 half

  • The ratio of frequencies squared is equal to the ratio of intensities because intensity and frequency squared are proportional

f subscript Q squared over f subscript P squared space equals space 1 fourth space equals space I subscript Q over I subscript P

I subscript Q space equals space 1 fourth I subscript P

  • So Q's lower frequency decreases its intensity by a factor of 4

Step 4: Determine the intensity of wave P in terms of I0 :

  • P has a lower amplitude which reduces its intensity by a factor of 4 compared to Q

  • However, P has a higher frequency which increases its intensity by a factor of 4 compared to Q

  • These effects cancel out, so wave P has an intensity of I0 , which is equal to that of wave Q

Examiner Tips and Tricks

The key concept with intensity is that it has an inverse square relationship with distance (not a linear one). This means the energy of a wave decreases very rapidly with increasing distance

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:The Wave EquationNext:Transverse & Longitudinal Waves
    Author
    Reviewer
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.