A LevelPhysicsCIERevision Notes21. Alternating Currents21.1 Properties and Uses of Alternating Current21.1.3 Mean Power

Syllabus Edition

First teaching 2020

Last exams 2024

|

Mean Power (CIE A Level Physics)

Revision Note

Test yourself
Katie M

Author

Katie M

Last updated

Mean Power

  • In mains electricity, current and voltage are varying all the time
  • This also means the power varies constantly, recall the equations for power:

P space equals space I V space equals space I squared R space equals space V squared over R

  • Where:
    • I = direct current (A)
    • V = direct voltage (V)
    • R = resistance (Ω)

  • The r.m.s values means equations used for direct current and voltage can now be applied to alternating current  and voltage
  • These are also used to determine an average current or voltage for alternating supplies
  • Recall the equation for peak current:

I subscript 0 space equals space square root of 2 I subscript r. m. s end subscript

  • The peak (maximum) power and the mean (average) power are given by:

P subscript m e a n end subscript space equals space open parentheses I subscript r. m. s end subscript close parentheses squared R

P subscript p e a k end subscript space equals space I subscript 0 squared R

  • Peak power can be written in terms of r.m.s current as

P subscript p e a k end subscript space equals space open parentheses square root of 2 I subscript r. m. s end subscript close parentheses squared R

  • Therefore, peak power is related to mean power by:

2 open parentheses I subscript r. m. s end subscript close parentheses squared R space equals space 2 P subscript m e a n end subscript

P subscript m e a n end subscript space equals space P subscript p e a k end subscript over 2

  • Therefore, it can be concluded that:

The mean power in a resistive load is half the maximum power for a sinusoidal alternating current or voltage

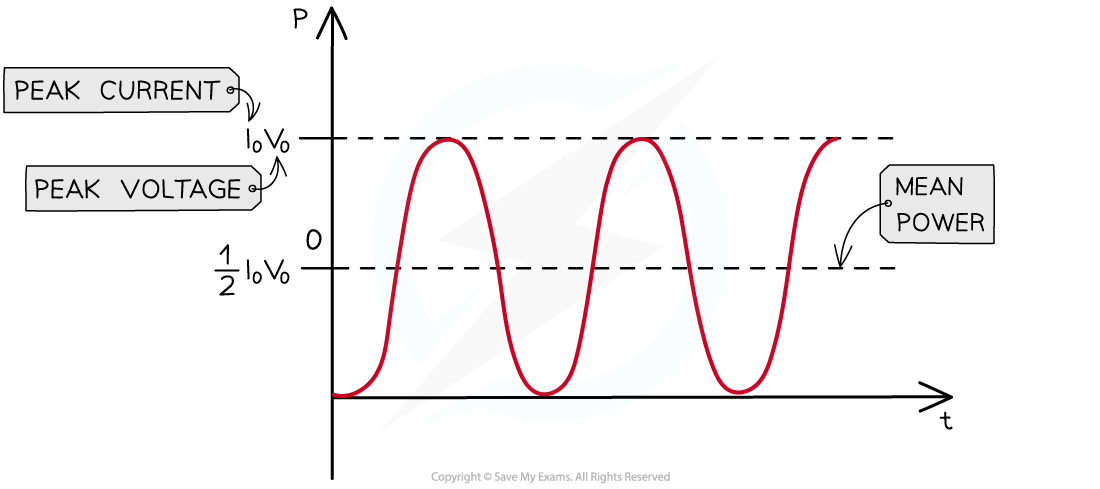
Average power graph, downloadable AS & A Level Physics revision notes

Mean power is exactly half the maximum power

Worked example

An alternating voltage supplied across a resistor of 40 Ω has a peak voltage V0 of 240 V.Calculate the mean power of this supply.

Step 1: Write down the known quantities

Resistance, R = 40 Ω

Peak voltage, V0 = 240 V

Step 2: Write out the equation for the peak power and calculate

Mean Power Worked Example equation 1

Mean Power Worked Example equation 2

Step 3: Calculate the mean power

        • The mean power is half of the maximum (peak) power

Mean power = 1440 / 2 = 720 W

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:21.1.2 Root-Mean-Square Current & VoltageNext:21.1.4 Rectification
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.