Electric Potential Energy (Cambridge (CIE) A Level Physics): Revision Note
Exam code: 9702
Electric potential energy of two point charges
When a charge moves through an electric field, work is done
The work done in moving a charge q is given by:
Where:
ΔW = work done (J)
q = magnitude of charge moving in the field (C)
ΔV = potential difference between two points (J C−1)
Work is done when
a positive charge in an electric field moves against the field lines
a negative charge moves with the field lines
Electrical potential difference
Two points at different distances from a charge will have different electric potentials
This is because the electric potential increases with distance from a negative charge and decreases with distance from a positive charge
Therefore, there will be an electric potential difference between the two points equal to:
Where:
Vf = final electric potential (J C−1)
Vi = initial electric potential (J C−1)
The potential difference due to a point charge can be written:
Where
Q = magnitude of point charge producing the potential
ε0 = permittivity of free space (F m−1)
rf = final distance from charge Q (m)
ri = initial distance from charge Q (m)
Electric potential energy
The electric potential energy of two point charges is given by:
Where:
Ep = electric potential energy (J)
Q1, Q2 = magnitudes of the charges (C)
r = distance between the centres of the two charges (m)
Similar to electric potential, values of electric potential energy depend on the signs of Q1 and Q2
By definition, potential V = 0 at infinity, therefore Ep = 0 at infinity
Like electric potential, the value of electric potential energy can be positive or negative
Change in electric potential energy
There is a change in electric potential energy when one charge moves away from another
This is because work must be done on the field to bring similar charges together or to separate opposite charges
Conversely, work is done by the field to separate similar charges or to bring opposite charges together
When a charge q moves away from a charge Q, the change in electric potential energy is equal to:
Where:
Q = charge that is producing the electric field (C)
q = charge that is moving in the electric field (C)
r1 = initial distance of q from the centre of Q (m)
r2 = final distance of q from the centre of Q (m)
Electric potential energy for moving charges
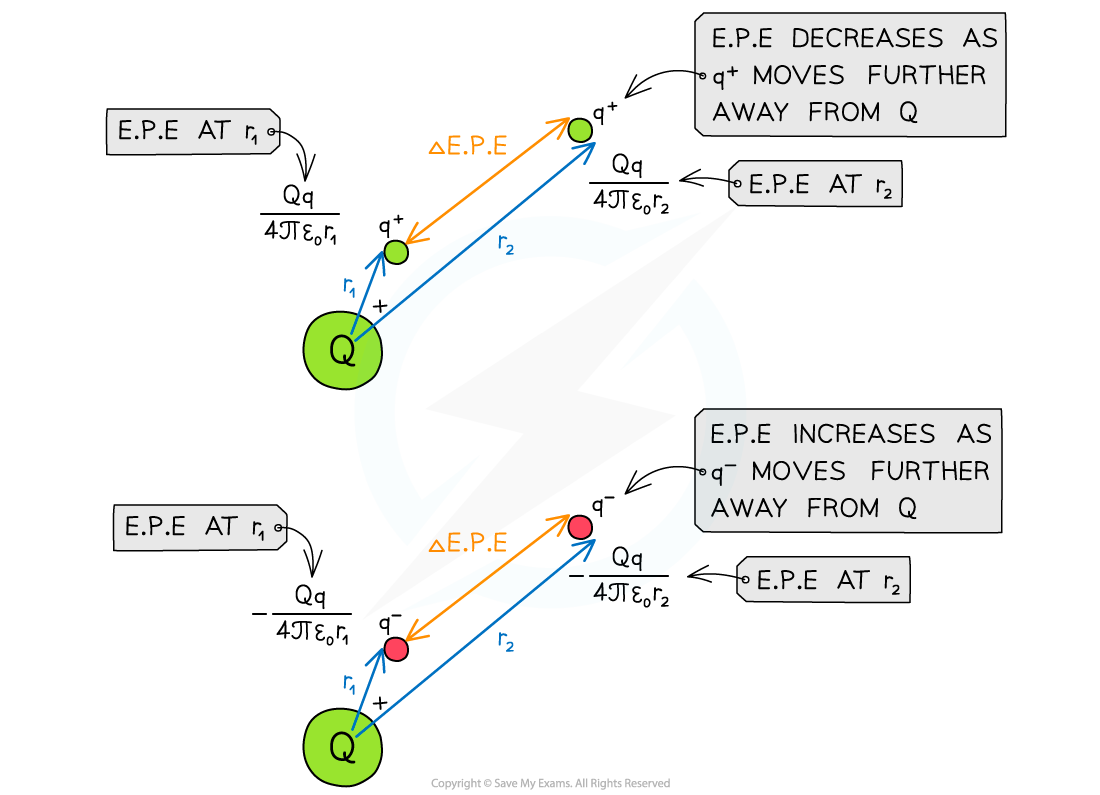
Work is done when moving a point charge away from another charge
The change in electric potential energy between two charges is analogous to the change in gravitational potential energy between two masses
Comparing gravitational and electric potential energy
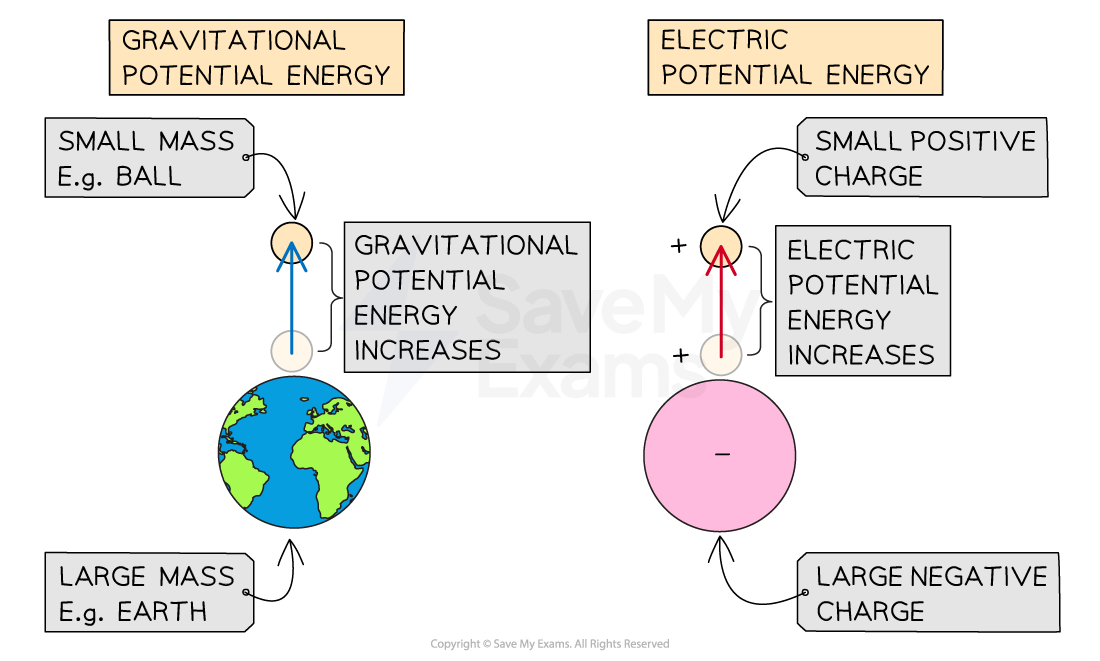
When a small mass is lifted on Earth, there is an increase in gravitational potential energy. This is similar to the increase in electric potential energy when a negative charge moves away from a positive charge
Worked Example
An α-particle is moving directly towards a stationary gold nucleus
.
At a distance of 4.7 × 10−15 m the α-particle momentarily comes to rest.
Calculate the electric potential energy of the particles at this instant.
Answer:
Step 1: Write down the known quantities
Distance, r = 4.7 × 10−15 m
Elementary charge, e = 1.60 × 10−19 C
Coulomb constant, k = 8.99 × 109 N m2 C−2
Step 2: Determine the magnitudes of the charges
An alpha particle (helium nucleus) contains 2 protons
Charge of alpha particle, q1 = 2e
The gold nucleus contains 79 protons
So, charge of gold nucleus, q2 = 79e
Step 3: Write down the equation for electric potential energy
Step 4: Substitute values into the equation
J (2 s.f.)
Examiner Tips and Tricks
This topic has a lot of concepts and language that can be easy to mix up, as well as many equations and graphs to learn. Take careful notes on this topic and learn the correct equations for each quantity, for example, when calculating electric potential energy, make sure you do not square the distance!
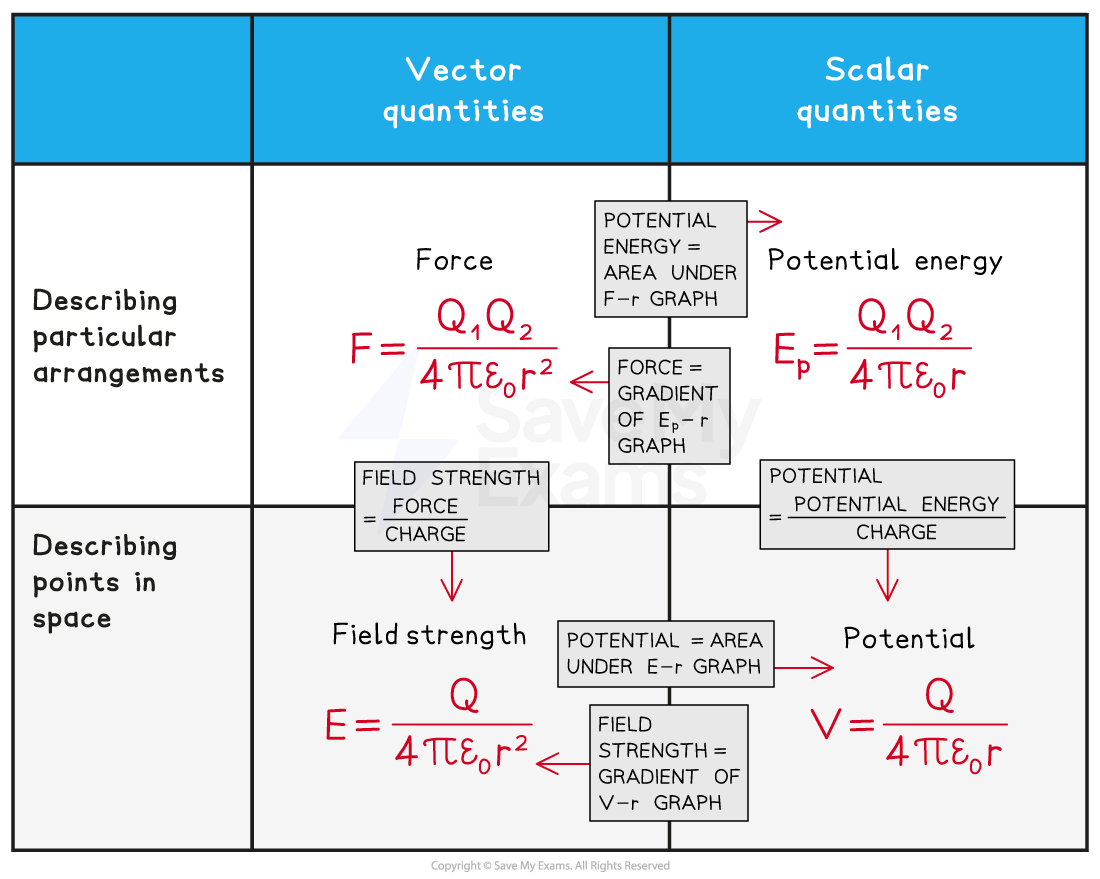
A good way to revise these is to find a way of organising the knowledge in a way that resonates with you, here is an example of one possible way to do this:

Unlock more, it's free!
Did this page help you?