SHM Graphs (Cambridge (CIE) A Level Physics): Revision Note
Exam code: 9702
SHM graphs
The displacement, velocity and acceleration of an object in simple harmonic motion can be represented graphically against time
The graphs of all undamped SHM oscillations are represented as periodic functions
This means they can all be described by sine and cosine curves
You need to know what each graph looks like and how it relates to the other graphs
Remember that:
Velocity is the rate of change of displacement
Acceleration is the rate of change of velocity
When oscillations start from the equilibrium position then:
The displacement-time graph is a sine curve
The velocity-time graph is the gradient of the displacement-time graph, so a cosine graph and 90o out of phase with the displacement-time graph
The acceleration-time graph is the gradient of the velocity-time graph, so a negative sine graph and 90o out of phase with the velocity-time graph
More information on this can be found in the IGCSE Maths revision notes on differentiation and CIE A level Maths pure 3 revision notes on differentiating other functions
Graphs of displacement, velocity and acceleration against time
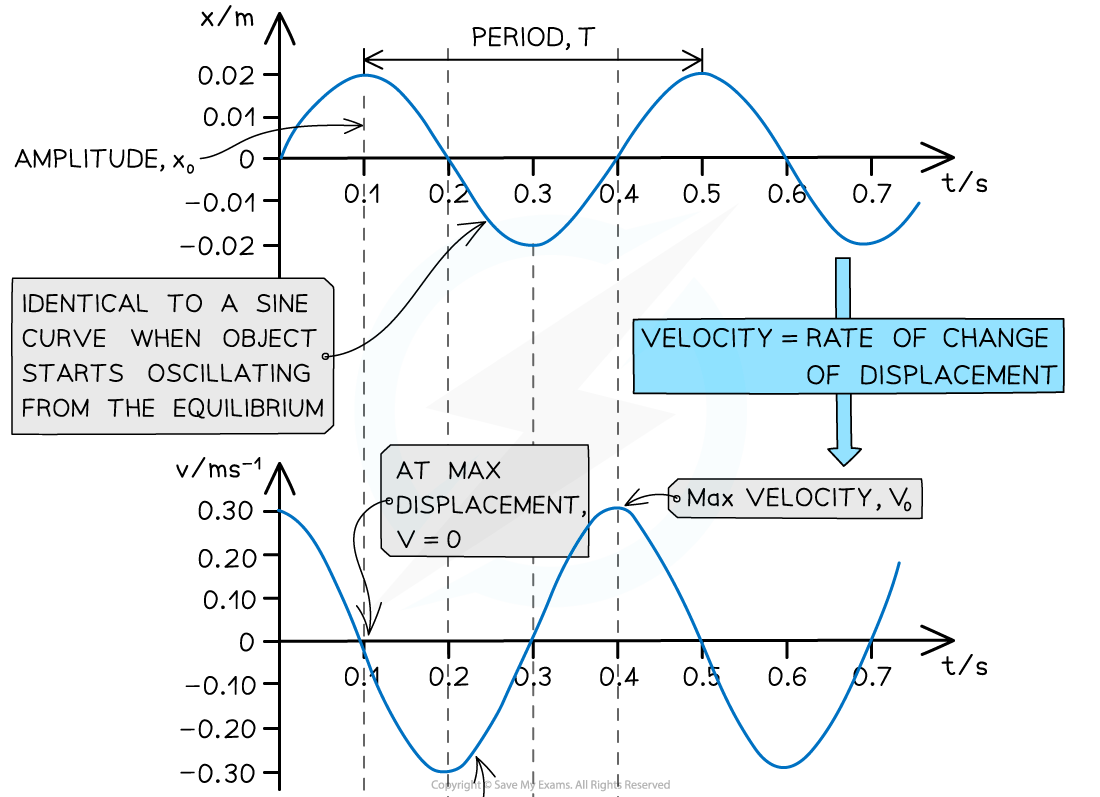
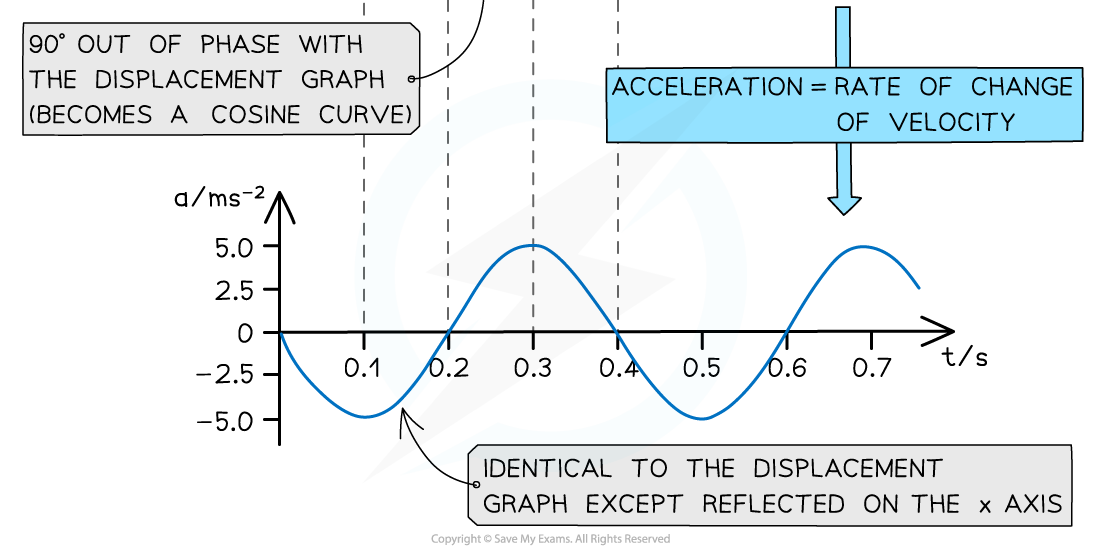
The displacement, velocity and acceleration graphs in SHM are all 90° out of phase with each other
Relationship between graphs
Key features of the displacement-time graphs:
The amplitude of oscillations A is the maximum value of x
The time period of oscillations T is the time taken for one full wavelength cycle
Key features of the velocity-time graphs:
The velocity of an oscillator at any time can be determined from the gradient of the displacement-time graph:

An oscillator moves the fastest at its equilibrium position
Therefore, the velocity is at its maximum when the displacement is zero (the amplitude of the graph is vmax)
Key features of the acceleration-time graph:
The acceleration graph is a reflection of the displacement graph in the x-axis
This means when a mass has positive displacement (to the right) the acceleration is in the opposite direction (to the left) and vice versa (from a = −ω2x)
The acceleration of an oscillator at any time can be determined from the gradient of the velocity-time graph:

The maximum value of the acceleration is when the oscillator is at its maximum displacement
Worked Example
A swing is pulled 5 cm and then released. The variation of the horizontal displacement x of the swing with time t is shown on the graph below.
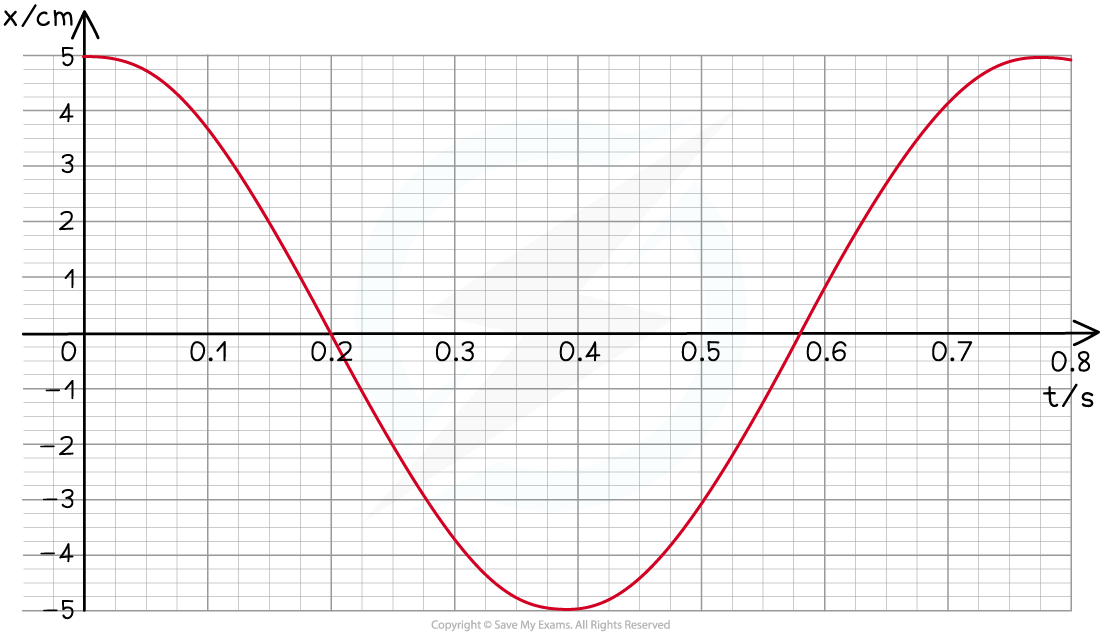
The swing exhibits simple harmonic motion.
Use data from the graph to determine at what time the velocity of the swing is first at its maximum.
Answer:
Step 1: The velocity is at its maximum when the displacement x = 0
Step 2: Reading value of time when x = 0
From the graph, this is equal to 0.2 s
Examiner Tips and Tricks
These graphs might not look identical to what is in your textbook, depending on where the object starts oscillating from at t = 0 (on either side of the equilibrium, or at the equilibrium). However, if there is no damping, they will all always be general sine or cosine curves.

Unlock more, it's free!
Did this page help you?