Average Kinetic Energy of a Molecule (CIE A Level Physics)

• An important property of molecules in a gas is their average kinetic energy
• This can be deduced from the ideal gas equations relating pressure, volume, temperature and speed
• Recall the ideal gas equation:

pV = NkT

• Also recall the equation linking pressure and mean square speed of the molecules:

• The left hand side of both equations are equal (pV)
• This means the right hand sides are also equal:

• N will cancel out on both sides and multiplying by 3 obtains the equation:

m<c²> = 3kT

• Recall the familiar kinetic energy equation from mechanics:

• Instead of v² for the velocity of one particle, <c²> is the average speed of all molecules

• Multiplying both sides of the equation by ½ obtains the average translational kinetic energy of the molecules of an ideal gas:

• Where:
  • E_K = kinetic energy of a molecule (J)
  • m = mass of one molecule (kg)
  • <c²> = mean square speed of a molecule (m² s^-2)
  • k = Boltzmann constant
  • T = temperature of the gas (K)

• Note: this is the average kinetic energy for only one molecule of the gas
• A key feature of this equation is that the mean kinetic energy of an ideal gas molecule is proportional to its thermodynamic temperature

E_K ∝ T

• Translational kinetic energy is defined as:

The energy a molecule has as it moves from one point to another

• A monatomic (one atom) molecule only has translational energy, whilst a diatomic (two-atom) molecule has both translational and rotational energy

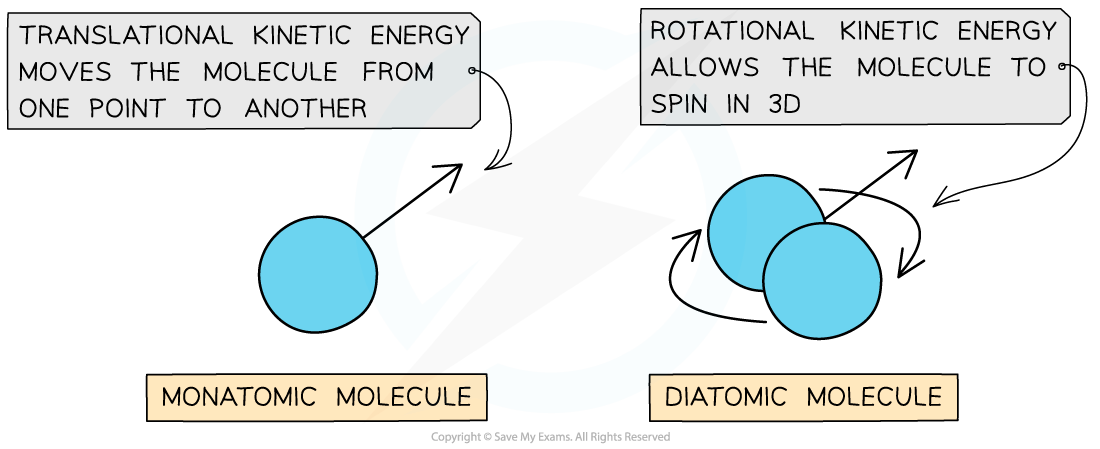
A diatomic molecule has both rotational and translational kinetic energy

Step 1:            Write down the equation for the average translational kinetic energy:

Step 2:            Find the relation between c_r.m.s and temperature T

Since m and k are constant, <c²> is directly proportional to T

<c²> ∝ T

Therefore, the relation between c_r.m.s and T is:

Step 3:            Write the equation in full

where a is the constant of proportionality

Step 4:            Calculate the constant of proportionality from values given by rearranging for a:

T = 45 ^oC + 273.15 = 318.15 K

Step 5:            Calculate c_r.m.s  at 80 ^oC by substituting the value of a and new value of T

T = 80 ^oC + 273.15 = 353.15 K