A gymnast dismounts from an exercise in which he swings on a high bar. The gymnast rotates in the air before landing.
Figure 1 shows the gymnast in three positions during the dismount.
Figure 1
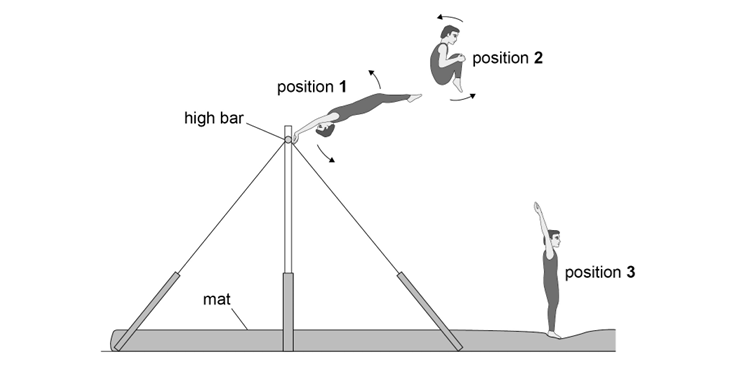
The arrows show the direction of rotation of the gymnast.
In position 1 the gymnast has just let go of the bar. His body is fully extended.
Position 2 shows the rotating gymnast a short time later. His knees have been brought close to his chest into a ‘tuck’.
Position 3 is at the end of the dismount as the gymnast lands on the mat. His body is once again fully extended.
Explain why the moment of inertia about the axis of rotation decreases when his knees are moved towards his chest.
Go on to explain the effect this has on his angular speed.
Table 1 gives some data about the gymnast in position 1 and in position 2.
Table 1
Position | Moment of inertia / kg m2 | Angular speed / rad s−1 |
|---|---|---|
1 | 13.5 | |
2 | 4.1 | 14.2 |
Calculate the angular speed of the gymnast in position 1.
The gymnast stays in the tuck for 1.2 s.
Determine the number of complete rotations performed by the gymnast when in the tuck during the dismount.
The gymnast repeats the exercise. The height of the bar remains unchanged.
State and explain two actions the gymnast can take to complete more rotations during the dismount.
Did this page help you?








