A LevelPhysicsAQARevision NotesAstrophysicsCosmologyThe Doppler Effect of Light

The Doppler Effect of Light (AQA A Level Physics)

Revision Note

Test yourself
Katie M

Author

Katie M

Last updated

The Doppler Effect of Light

  • The Doppler shift for a light-emitting non-relativistic (v << c) source can be described using the equation:

fraction numerator increment f over denominator f end fraction space equals space fraction numerator increment lambda over denominator lambda end fraction space almost equal to fraction numerator increment v over denominator c end fraction

  • Where:

    • increment f = change in frequency (Hz)

    • space f = reference frequency (frequency of the source) (Hz)

    • increment lambda = change in wavelength (m)

    • space lambda = reference wavelength (wavelength of the source) (m)

    • increment v = relative velocity of the source and observer (m s–1)

    • space c = the speed of light (m s–1)

  • The change in wavelength increment lambda is equal to:

increment lambda space equals space lambda apostrophe space minus space lambda

  • Where:

    • lambda apostrophe = observed wavelength of the source (m)

  • The relative speed between the source and observer along the line joining them is given by:

increment v space equals space v subscript s space minus space v subscript o

  • Where:

    • v subscript s = velocity of the light source (m s–1)

    • v subscript o = velocity of the observer (m s–1)

  • The velocity of the observer (usually from Earth) can be assumed to be stationary, i.e. v subscript o space equals space 0

  • The relative speed then simply becomes the speed of the source:

 increment v space equals space v subscript s space equals space v

  • Hence, the Doppler shift equation can be written as:

fraction numerator increment f over denominator f end fraction space equals space fraction numerator lambda apostrophe space minus space lambda over denominator lambda end fraction space equals space fraction numerator increment lambda over denominator lambda end fraction space equals space v over c

Redshift

  • The fractional change in the wavelength fraction numerator increment lambda over denominator lambda end fraction is called the redshift and is given the symbol z

  • In terms of wavelength, redshift is given by:

z space equals space fraction numerator increment lambda over denominator lambda end fraction space equals space minus v over c

  • In terms of frequency, redshift is given by:

z space equals space minus fraction numerator increment f over denominator f end fraction space equals space v over c

  • This shows that if the source moves away from the observer then

    • The wavelength increases

    • The frequency decreases

  • Note: the sign of z  can cause some confusion, remember to look at the context - z  is a measure of redshift so write it as positive for receding objects

Doppler Shift of Light

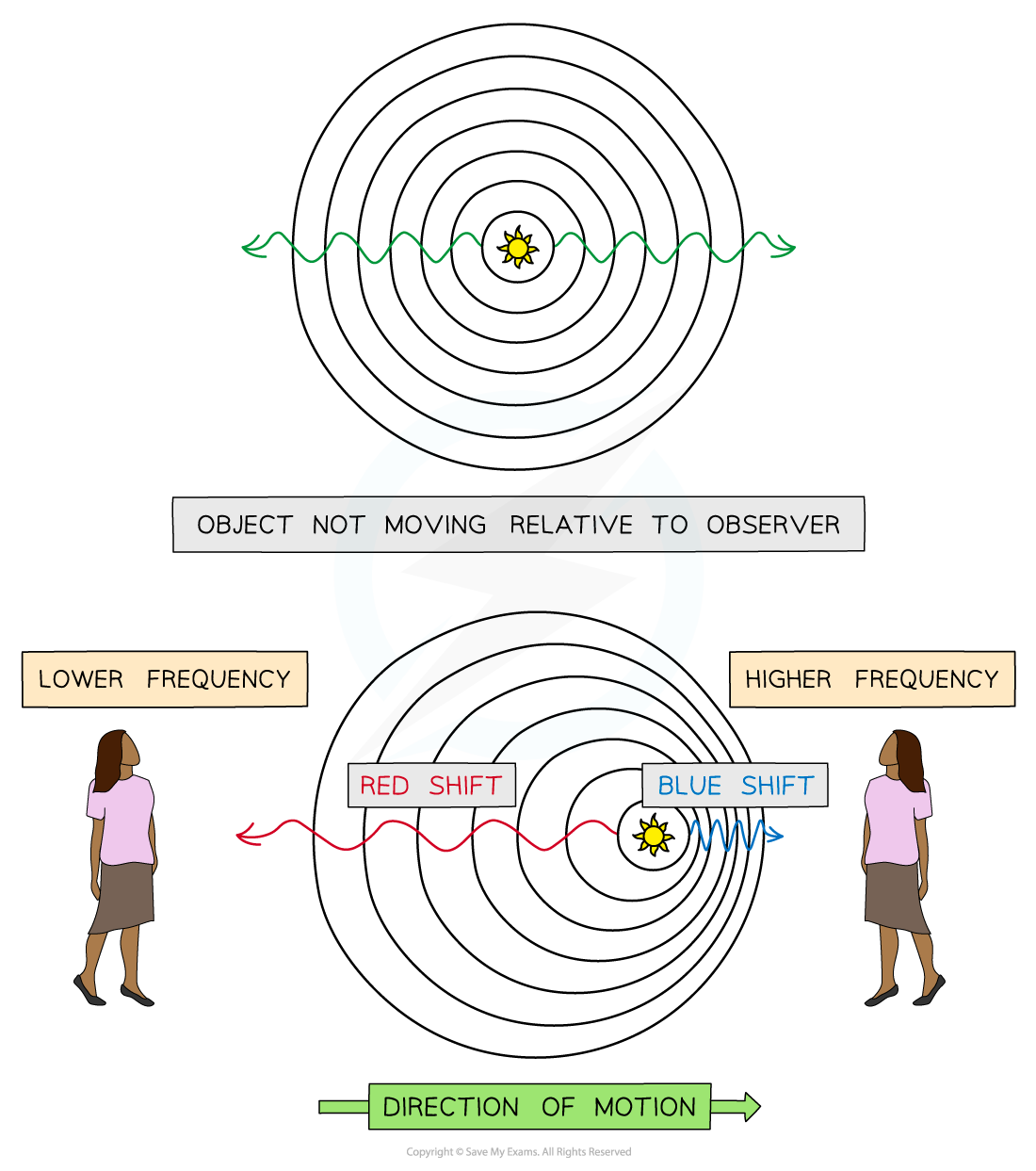
Light Doppler Shift

  • Doppler shift can be observed in the spectra of stars and galaxies

  • If the star is approaching the Earth, blueshift is observed (negative z)

    • The relative velocity v is positive

    • The change in wavelength increment lambda is negative

  • If the star is receding from the Earth, redshift is observed (positive z)

    • The relative velocity v is negative

    • The change in wavelength increment lambda is positive

Worked Example

A stationary source of light is found to have a spectral line of wavelength 438 nm.  The same line from a distant star that is moving away from the Earth has a wavelength of 608 nm.

Calculate the speed at which the star is travelling away from the Earth.

Answer:

Step 1: List the known quantities

  • Unshifted wavelength, λ = 438 nm

  • Shifted wavelength, λ' = 608 nm

  • Change in wavelength, Δλ = (608 – 438) nm = 170 nm 

  • Speed of light, c = 3.0 × 108 m s–1

Step 2: Write down the Doppler equation and rearrange for velocity v

fraction numerator increment lambda over denominator lambda end fraction space equals space v over c

v space equals space fraction numerator c increment lambda over denominator lambda end fraction

Step 3: Substitute values to calculate v

v space equals space fraction numerator left parenthesis 3.0 blank cross times blank 10 to the power of 8 right parenthesis cross times 170 over denominator 438 end fraction = 1.16 × 108 m s–1

Worked Example

The stars in a distant galaxy can be seen to orbit about a galactic centre. The galaxy can be observed 'edge-on' from the Earth.

Light emitted from a star on the left-hand side of the galaxy is measured to have a wavelength of 656.44 nm. The same spectral line from a star on the right-hand side is measured to have a wavelength of 656.12 nm.

The wavelength of the same spectral line measured on Earth is 656.28 nm.

(a) State and explain which side of the galaxy is moving towards the Earth.

(b) Calculate the rotational speed of the galaxy.

Answer:

Part (a)

  • The light from the right-hand side (656.12 nm) is observed to be at a shorter wavelength than the reference line (656.28 nm)

  • Therefore, the right-hand side shows blueshift and must, therefore, be moving towards the Earth

Part (b)

Step 1: List the known quantities

  • Observed wavelength on LHS, lambda subscript L H S end subscript = 656.44 nm

  • Observed wavelength on RHS, lambda subscript R H S end subscript = 656.12 nm

  • Reference wavelength, λ = 656.28 nm

  • Speed of light, c = 3.0 × 108 m s−1

Step 2: Calculate the average change in wavelength

  • The magnitude of redshift or blueshift from each side is different, so you must calculate the average

increment lambda space equals space fraction numerator lambda subscript L H S end subscript space minus space lambda subscript R H S end subscript over denominator 2 end fraction space equals space fraction numerator 656.44 space minus space 656.12 over denominator 2 end fraction

increment lambda space= 0.16 nm

  • Tip: you don't need to change the wavelengths from nm to m, as the units will cancel out later

Step 3: Write down the Doppler equation and rearrange for velocity v

fraction numerator increment lambda over denominator lambda end fraction space equals space v over c

v space equals space fraction numerator c increment lambda over denominator lambda end fraction

Step 4: Substitute values into the velocity equation

v space equals space fraction numerator open parentheses 3 cross times 10 to the power of 8 close parentheses space cross times space 0.16 over denominator 656.28 end fraction

Rotational speed:  v space equals space 7.31 space cross times 10 to the power of 4 space straight m space straight s to the power of negative 1 end exponent space equals space 73 space km space straight s to the power of negative 1 end exponent

Examiner Tips and Tricks

You need to recall that, in the visible light spectrum, red light has a longer wavelength and a lower frequency compared to blue light which has a shorter wavelength and a higher frequency

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:The Hertzsprung-Russell DiagramNext:Binary Star Systems
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.