Wien’s Displacement Law

All bodies emit a spectrum of thermal radiation in the form of electromagnetic waves

An ideal black-body radiator is one that absorbs and emits all wavelengths
- A perfect black-body radiator is a theoretical object
- However, stars are the best approximation there is

The radiation emitted from a black body has a characteristic spectrum that is determined by the temperature alone
This can be represented on a black-body radiation curve of intensity against wavelength
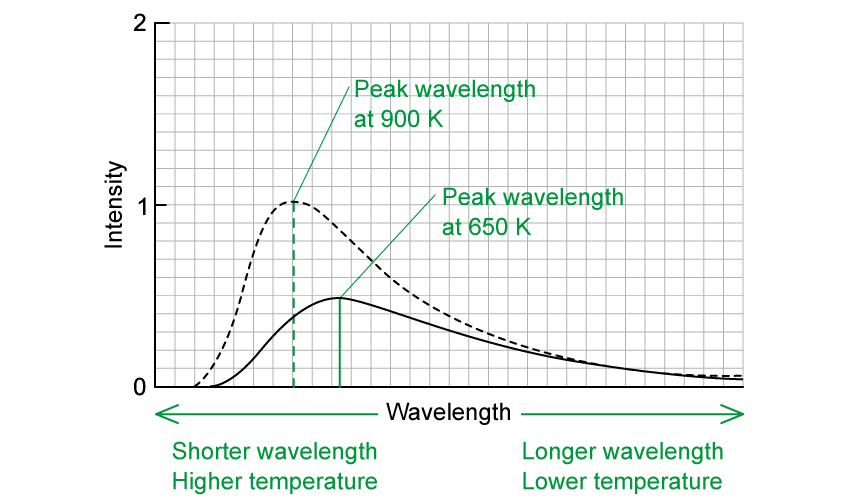
- As the temperature increases, the peak of the curve moves
- This moves to a lower wavelength and a higher intensity

Black-body radiators at different temperatures

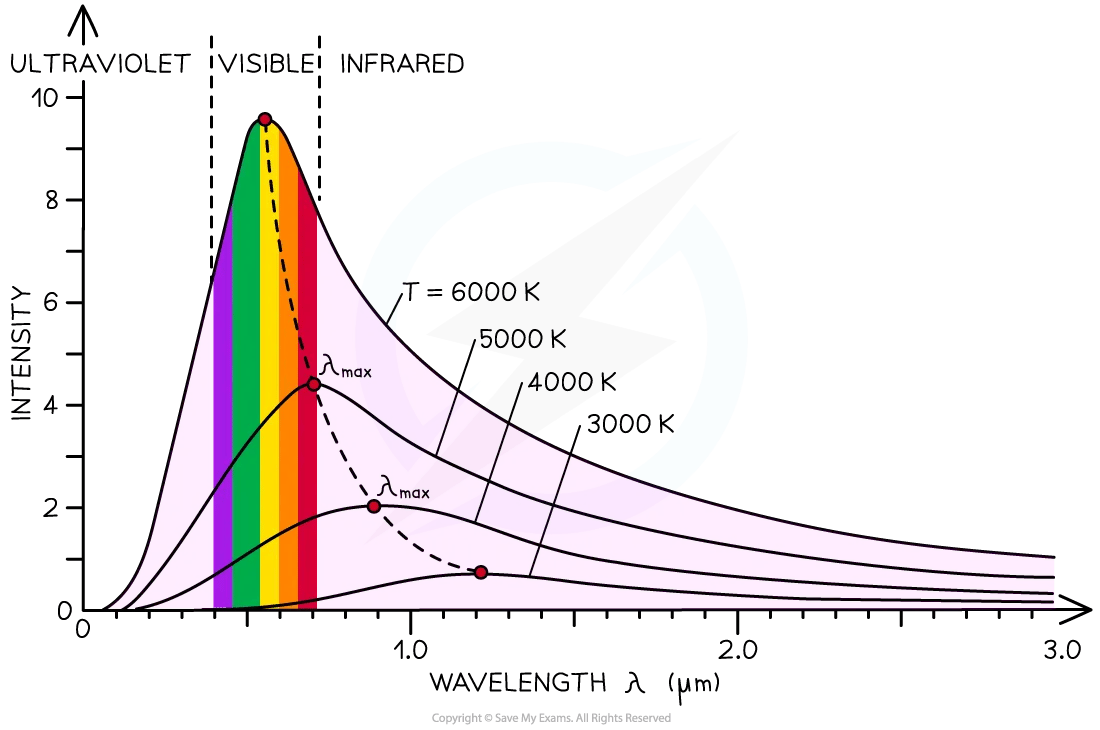
Wien's Displacement Law Graph, for IB Physics Revision Notes

The intensity-wavelength graph shows how thermodynamic temperature links to the peak wavelength for four different bodies

Wien’s displacement law relates the observed wavelength of light from an object to its surface temperature, it states:

The black body radiation curve for different temperatures peaks at a wavelength that is inversely proportional to the temperature

This relation can be written as:

$λ_{m a x} \propto \frac{1}{T}$

Where:
- λ_max = the maximum wavelength emitted by an object at the peak intensity (m)
- T = the surface temperature of an object (K)

Wien's displacement law can be written as:

λ_maxT = 2.9 × 10⁻³ m K

This equation shows that the higher the temperature of a body...
- The shorter the wavelength at the peak intensity (i.e. hotter objects tend to be white or blue, and cooler objects tend to be red or yellow)
- The greater the intensity of the radiation at each wavelength

Table to compare surface temperature and star colour

Star Colour	Temperature / K
blue	>33 000
blue-white	10 000 − 30 000
white	7500 − 10 000
yellow-white	6000 − 7500
yellow	5000 − 6000
orange	3500 − 5000
red	<3500

Worked example

The black-body radiation curve of an object at 900 K is shown in the diagram below.

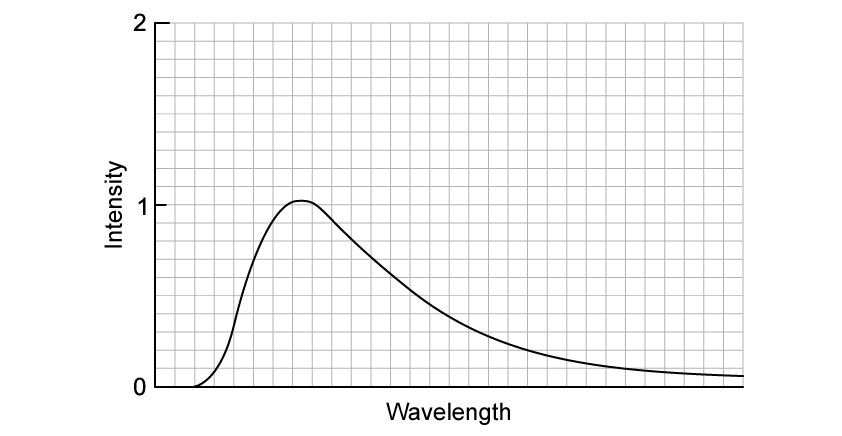
2-1-15-wiens-displacement-law-worked-example-graph-ib-2025-physics

Which of the following shows the black-body radiation curve of an object at 650 K?

The dashed line represents the curve of the object at 900 K.

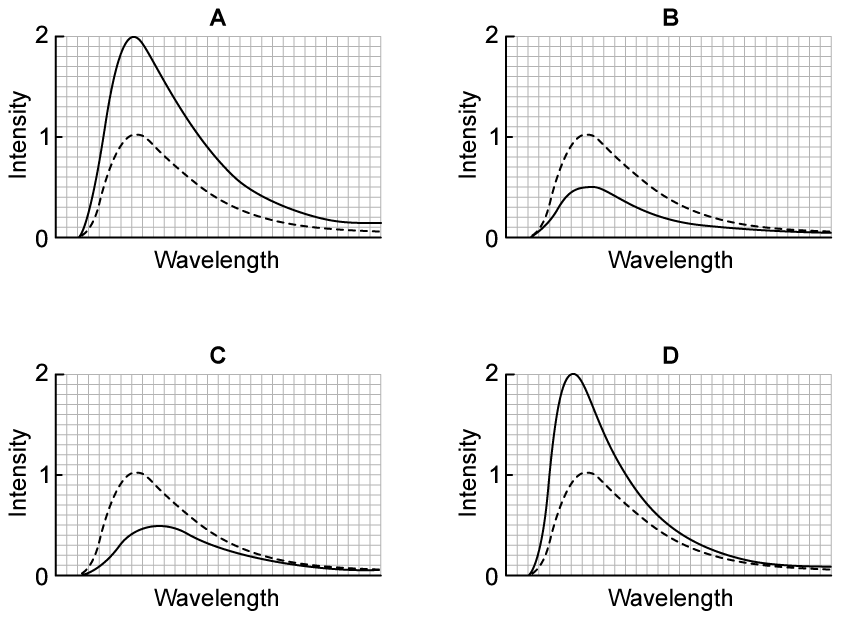
2-1-15-wiens-displacement-law-worked-example-graph-options

Answer: C

From Wien's displacement law: $λ_{m a x} \propto \frac{1}{T}$
Therefore, a curve with a longer peak wavelength will correspond to a lower temperature

Worked example

The spectrum of the star Rigel in the constellation of Orion peaks at a wavelength of 263 nm, while the spectrum of the star Betelgeuse peaks at a wavelength of 828 nm.

Determine which of these two stars, Betelgeuse or Rigel, is cooler.

Answer:

Step 1: List the known quantities

Maximum emission wavelength of Rigel = 263 nm = 263 × 10⁻⁹ m
Maximum emission wavelength of Betelgeuse = 828 × 10⁻⁹ m

Step 2: Write down Wien’s displacement law and rearrange for temperature T

$λ_{m a x} T = 2.9 \times 10^{- 3} m K$

$T = \frac{2.9 \times 10^{- 3}}{λ_{m a x}}$

Step 3: Calculate the surface temperature of each star

Rigel: $T = \frac{2.9 \times 10^{- 3}}{263 \times 10^{- 9}} = 11 027 = 11 000 K$

Betelgeuse: $T = \frac{2.9 \times 10^{- 3}}{828 \times 10^{- 9}} = 3502 = 3500 K$

Step 4: Write a concluding sentence

Betelgeuse has a surface temperature of 3500 K, therefore, it is much cooler than Rigel

Wien's law and stars in the Orion constellation

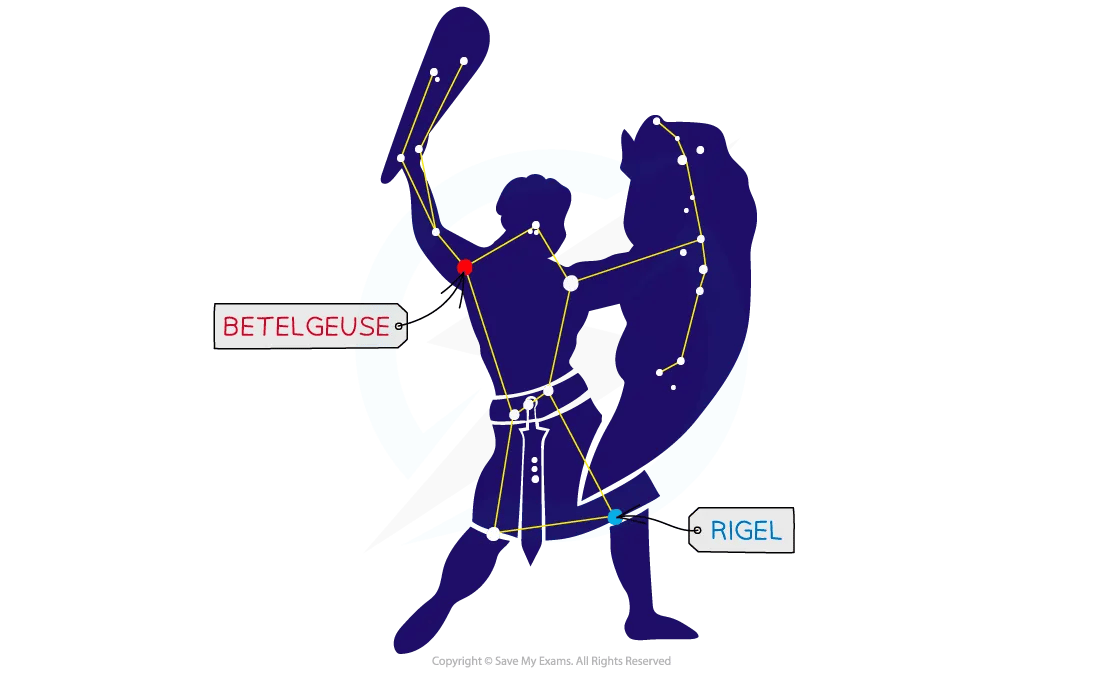
Wien's Law Orion and Betelguese Worked Example, for IB Physics Revision Notes

The Orion Constellation; cooler stars, such as Betelgeuse, appear red or yellow, while hotter stars, such as Rigel, appear white or blue

Examiner Tip

Note that the temperature used in Wien’s Law is in Kelvin (K). Remember to convert from °C if the temperature is given in degrees in the question before using the Wien’s Law equation.

If you're asked to draw a black-body curve in the exam, make sure to avoid these common errors:

Drawing the right side of the curve steeper than the left side (remember it increases sharply and decreases more steadily)
Drawing the right side of the curve so that it decreases to zero (it should not meet zero as it decreases)
Drawing the curve through the intensity axis (there are no negative wavelengths!)

Wien’s Displacement Law (AQA A Level Physics)

Revision Note