Absolute Magnitude (AQA A Level Physics)

Absolute Magnitude

• The inherent brightness, or intensity of a star, as seen to the naked eye on Earth, depends on its:

  • Luminosity

  • Distance from Earth

• If two different stars have the same apparent magnitude it does not necessarily mean they emit the same amount of light or are the same size

  • Therefore, it's useful to compare how bright they would appear to be if they were exactly the same distance from the Earth

  • This is where the concept of absolute magnitude comes in

• The absolute magnitude of a star is defined as:

  The apparent magnitude it would have if it were observed from a distance of 10 parsecs away from Earth

• Since most stars are much further than 10 parsecs away, they would appear brighter if observed at a distance of 10 parsecs

Apparent vs. absolute magnitude

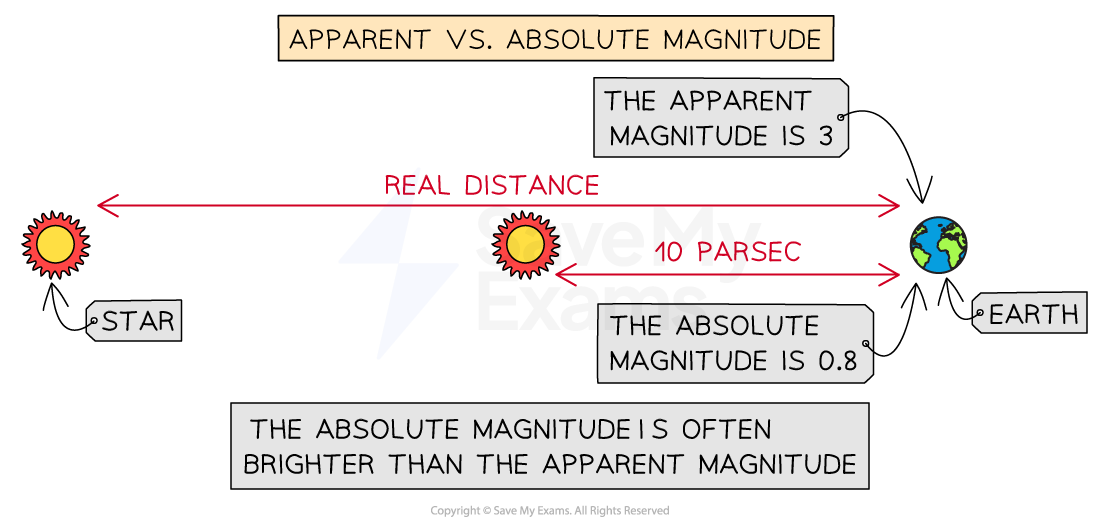
The absolute magnitude is often brighter than the apparent magnitude

• For example, a real bright star very far away would have the same apparent magnitude as a dim star close by

  • However, their absolute magnitudes will be different

• This means that:

  • Absolute and apparent magnitudes are measured on the same logarithmic scale

  • Values of absolute magnitudes are more negative than their associated apparent magnitudes

• The relationship between the apparent magnitude, absolute magnitude and distance of a star from Earth is:

• Where:

  • M = absolute magnitude

  • m = apparent magnitude

  • d = distance of the star from Earth (measured in parsecs)

• The difference between apparent and absolute magnitude is known as the distance modulus

• This is useful for quickly determining the relative distance of a star

  • Distance modulus is negative for stars closer than 10 pc

  • Distance modulus is positive for stars further away than 10 pc