Neutron Stars & Black Holes | AQA A Level Physics Revision Notes 2017

Neutron Stars

Neutron stars are objects which form after a supernova has ejected the outer layers of a star into space
- A core which has a mass between 1.4 and 3 solar masses will become a neutron star

A neutron star is defined as:

An extremely dense collapsed star made up of neutrons

Neutron stars are extremely small and dense (~10¹⁷ kg m⁻³)
- A neutron star with the mass of the Sun would have a diameter of about 30 km
- A teaspoon of neutron star would have a mass of about 100 million tonnes

The immense gravitational forces acting on the core crush the electrons and protons until they combine into neutrons, via reverse beta decay:

$p + e^{-} \to n + ν$

Further collapse is prevented by neutron degeneracy pressure

Some neutron stars rotate rapidly (up to 600 times per second) emitting bursts of highly directional electromagnetic radiation
- These stars are called pulsars

What is a pulsar?

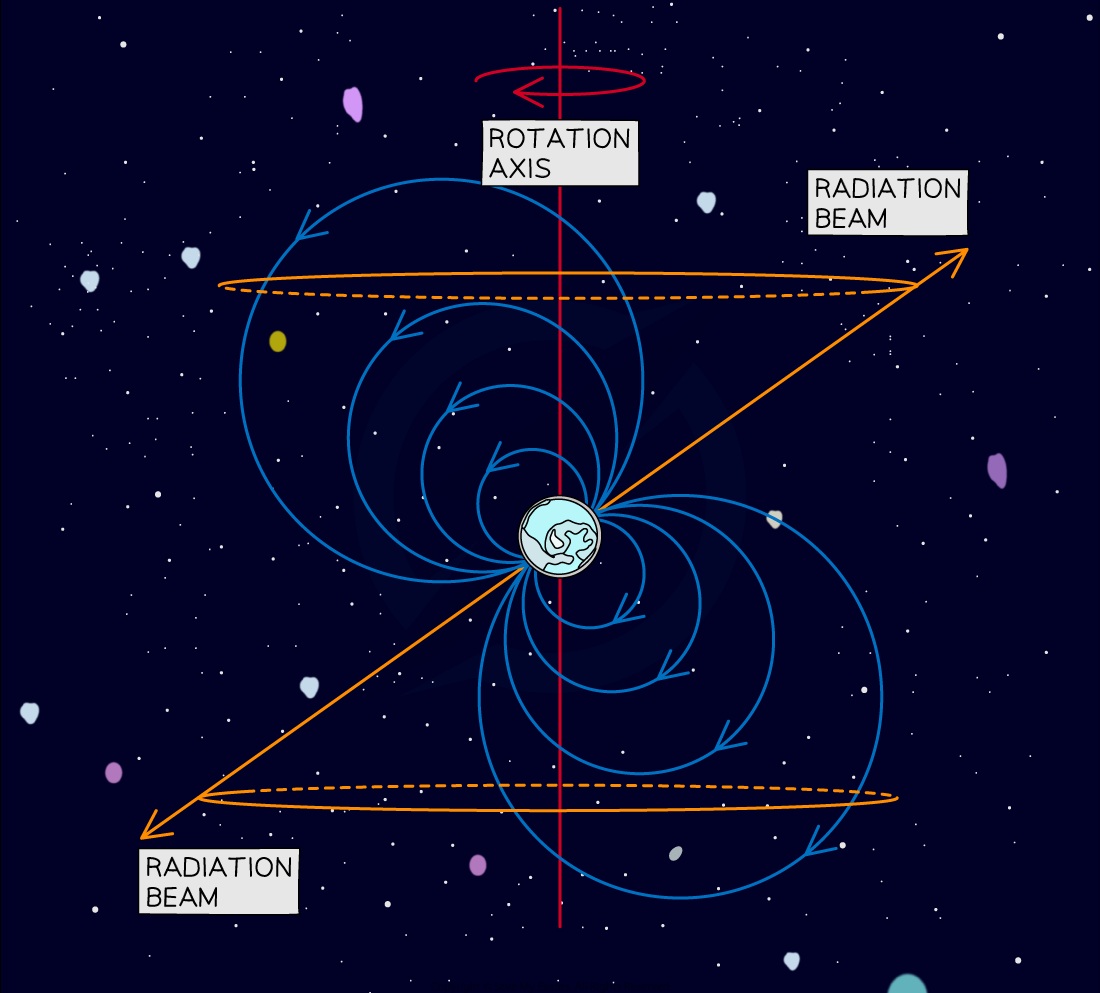
A fast-rotating neutron star is called a pulsar

Pulsars are much easier to identify than slow, or non-rotating, neutron stars
- This is because they emit radiation periodically which makes them easier to detect
- In particular, they emit radio waves strongly, and sometimes X-rays and gamma rays

Black Holes

After a supernova has ejected the outer layers of a star into space, the most massive cores can collapse into an infinitely dense point called a singularity
- A core which has a mass greater than 3 solar masses will become a black hole

The gravitational field around a black hole is so strong that nothing, not even light, can escape it

The boundary at which light and matter cannot escape the gravitational pull of the black hole is called the event horizon
The escape velocity beyond the event horizon is greater than the speed of light
- This is why black holes cannot be seen directly, as photons cannot escape beyond the event horizon

What is a black hole?

5-10-6-characteristics-of-a-black-hole_ocr-al-physics

A black hole is an object which is so dense that its escape velocity is greater than the speed of light

Schwarzchild Radius of a Black Hole

The radius of a black hole’s event horizon is called the Schwarzschild radius and is given by:

$R_{s} \approx \frac{2 G M}{c^{2}}$

Where:
- $R_{s}$ = the Schwarzschild radius (m)
- $G$ = gravitational constant
- $M$ = mass of the black hole
- $c$ = speed of light

Supermassive Black Holes

Observations of stars at the centre of the Milky Way suggest that a mass equivalent to millions of stars is contained in a very small volume
Astronomers determined that the mass at the galactic centre is, in fact, a supermassive black hole
- Sagitarrius A*, the one in our galactic centre, has a mass of 4 million solar masses

Since this discovery, over 150 supermassive black holes have been identified at the centres of other galaxies similar to the Milky Way
- This is thought to be strong evidence that supermassive black holes exist at the centres of nearly all large galaxies

Worked example

Some galaxies, known as Seyfert galaxies, have very active galactic centres. They are believed to host supermassive black holes at their centres.

The black hole at the centre of the galaxy NGC 5252 is found to have a mass 9.5 × 10⁹ times that of the Sun.

(a)

Explain what is meant by the ‘event horizon’ of a black hole.

(b)

Calculate the radius of the event horizon in terms of solar radii.

(c)

Calculate the average density of matter inside the event horizon.

(d)

Compare your answer to (c) with the density of a black hole which has the same mass as the Sun.

Answer:

(a) An event horizon is:

The boundary of the region around a black hole inside of which light cannot escape

(b)

Step 1: List the known quantities

Mass of the black hole, $M$ = 9.5 × 10⁹ $M_{☉}$
Mass of the Sun, $M_{☉}$ = 1.99 × 10³⁰ kg (from the data booklet)
Gravitational constant, $G$ = 6.67 × 10^–11 N m² kg^–2 (from the data booklet)
Speed of light, $c$ = 3.00 × 10⁸ m s^–1 (from the data booklet)
Radius of the Sun, $R_{☉}$ = 6.96 × 10⁸ m (from the data booklet)

Step 2: Write down the equation for the Schwarzschild radius

$R_{s} = \frac{2 G M}{c^{2}}$

Note: this equation is included in the data booklet

Step 3: Calculate the radius of the event horizon

$R_{s} = \frac{2 \times (6.67 \times 10^{- 11}) \times (9.5 \times 10^{9}) \times (1.99 \times 10^{30})}{{(3.00 \times 10^{8})}^{2}}$

Schwarzschild radius: $R_{S}$ = 2.8 × 10¹³ m

Step 4: Convert to solar radii

Schwarzschild radius: $R_{S} = \frac{2.8 \times 10^{13}}{6.96 \times 10^{8}} = 40 000 R_{☉}$

This means the size of the black hole is the equivalent length of 40,000 Suns placed side-by-side

(c)

Step 1: Recall the equations for density and volume

We can treat the volume of the black hole as a sphere:

$V = \frac{4}{3} π {R_{S}}^{3}$

The density of the black hole is therefore given by

$ρ = \frac{M}{V} = \frac{3 M}{4 π {R_{S}}^{3}}$

Step 2: Calculate the average density of the matter within the event horizon

$ρ = \frac{3 \times (9.5 \times 10^{9}) \times (1.99 \times 10^{30})}{4 π {\times (2.8 \times 10^{13})}^{3}} = 0.21 kg m^{- 3}$

(d)

Step 1: Write expressions for the densities and Schwarzschild radii of the black holes

Density of a solar-mass black hole:

$ρ_{1} = \frac{M_{☉}}{V_{1}} = \frac{3 M_{☉}}{4 π {R_{1}}^{3}}$

Where $R_{1} = \frac{2 G M_{☉}}{c^{2}}$

Density of a supermassive black hole:

$ρ_{2} = \frac{(9.5 \times 10^{9}) M_{☉}}{V_{2}} = (9.5 \times 10^{9}) \frac{3 M_{☉}}{4 π {R_{2}}^{3}}$

Where $R_{2} = (9.5 \times 10^{9}) \frac{2 G M_{☉}}{c^{2}}$

Step 2: Determine the ratio of the densities and make a comparison

$\frac{ρ_{1}}{ρ_{2}} = \frac{3 M_{☉}}{4 π {R_{1}}^{3}} \times \frac{1}{9.5 \times 10^{9}} \frac{4 π {R_{2}}^{3}}{3 M_{☉}}$

$\frac{ρ_{1}}{ρ_{2}} = \frac{1}{9.5 \times 10^{9}} {(\frac{R_{2}}{R_{1}})}^{3}$

Substituting $\frac{R_{2}}{R_{1}} = 9.5 \times 10^{9}$ :

$\frac{ρ_{1}}{ρ_{2}} = \frac{1}{9.5 \times 10^{9}} {(9.5 \times 10^{9})}^{3} = {(9.5 \times 10^{9})}^{2} = 9 \times 10^{19}$

This means that the solar-mass black hole is ~10²⁰ times denser than the supermassive black hole
The density of a black hole must be proportional to the inverse square of its mass, i.e. the more massive the black hole, the less dense it is

Examiner Tip

When writing the definition for the event horizon of a black hole, make sure to be clear that it is the boundary where the escape velocity = c

Avoid definitions that describe the event horizon as a point or a distance, as this is not correct.

Neutron Stars & Black Holes (AQA A Level Physics)

Revision Note

Neutron Stars

What is a pulsar?

Black Holes

What is a black hole?

Schwarzchild Radius of a Black Hole

Supermassive Black Holes

Worked example

Examiner Tip

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Katie M