Brightness & Apparent Magnitude

Apparent magnitude m is defined as

The perceived brightness of a star as seen from Earth

The value of m is a number with no unit
The Hipparcos scale of apparent magnitude initially classified brightness by assigning values from 1.0 to 6.0, where
- Magnitude 1.0 represented the brightest stars that could be seen with the naked eye
- Magnitude 6.0 represented dimmer stars that were only just visible to the naked eye

As astronomy progressed, the Hipparcos scale was able to be defined more precisely as a logarithmic scale
This allows stars to be compared meaningfully in terms of their brightness, or intensity, such that:

A magnitude 1 star is 100 times brighter than a magnitude 6 star

This means that a change of 5 orders of magnitude corresponds to:
- m = 6 → m = 1: an increase in brightness by a factor of $100$
- m = 1 → m = 6: a decrease in brightness by a factor of $100$

Therefore, for a change of 1 order of magnitude:
- Magnitude decreases by 1 (e.g. m = 6 → m = 5): brightness increases by a factor of $100^{\frac{1}{5}} \approx 2.51$
- Magnitude increases by 1 (e.g. m = 1 → m = 2): brightness decreases by a factor of $100^{\frac{1}{5}} \approx 2.51$

To compare the brightness of two objects, A and B, we can write an expression in terms of the ratio of their intensities:

$\frac{I_{A}}{I_{B}} = 2 . 51^{(m_{B} - m_{A})}$

Where:
- $I_{A}$ = intensity of object A (W m⁻²)
- $I_{B}$ = intensity of object B (W m⁻²)
- $m_{A}$ = apparent magnitude of object A
- $m_{B}$ = apparent magnitude of object B

The Relationship between Apparent Magnitude & Brightness

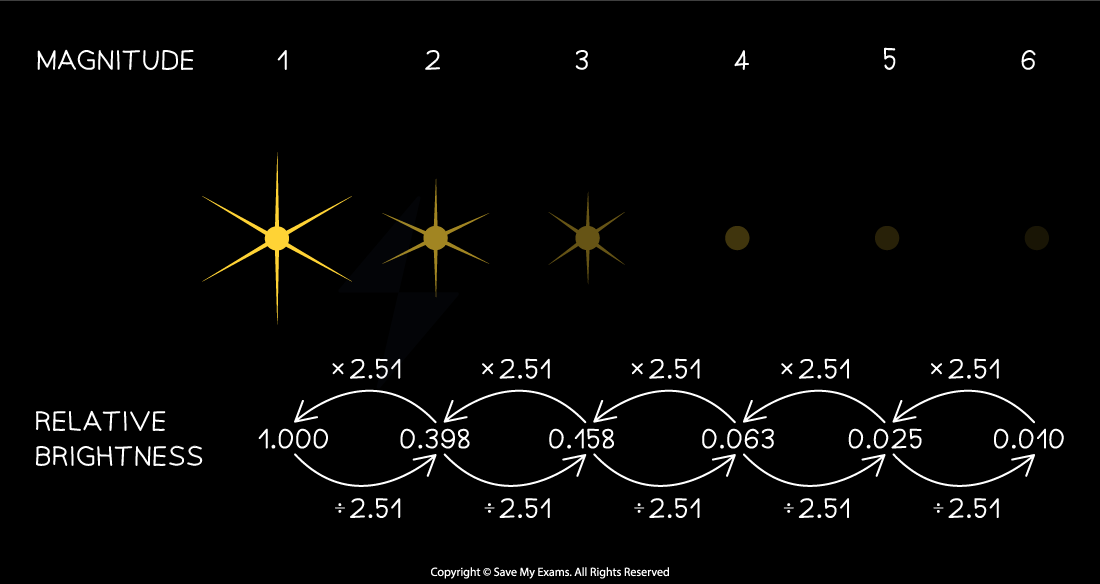
9-2-1-apparent-magnitude-and-brightness-scale

Each order of magnitude on the apparent brightness scale represents an increase or decrease in brightness by a factor of 2.51

Since the invention of the telescope, the scale has been expanded, so that
- The more negative the apparent magnitude, the brighter an object appears e.g. the Sun has an apparent magnitude of −26
- The more positive the apparent magnitude, the fainter an object appears e.g. Pluto has an apparent magnitude of 15

Apparent Magnitudes of Common Astronomical Objects

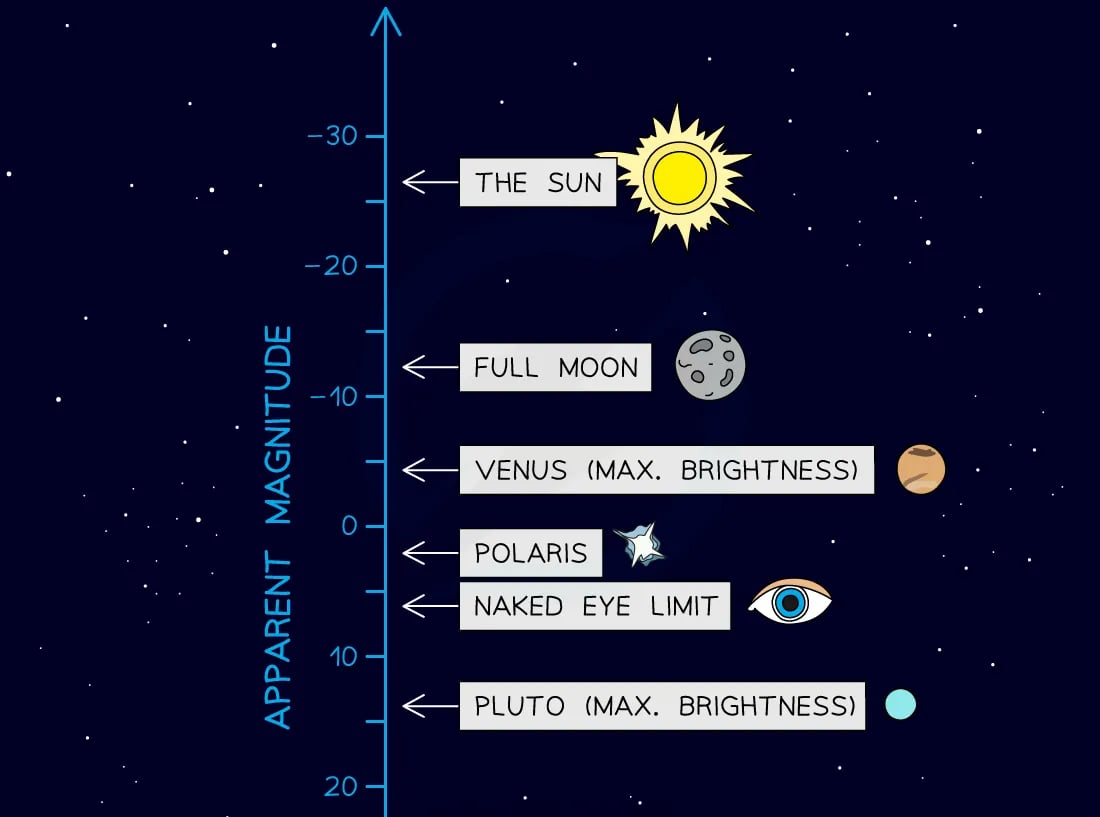
apparent-magnitude-scale-ib-physics-revision-notes

This scale shows that the most visible object in the sky is (unsurprisingly) the Sun and that objects such as Venus and the star Polaris are easy to spot with the naked eye, whereas Pluto is not

The full apparent magnitude scale is a powerful tool for comparing and quantifying differences in brightness
- For example, the naked eye can detect objects as faint as magnitude +6
- The Hubble Space Telescope (HST) can detect objects as faint as magnitude +31

This means that the faintest object that can be detected by the HST is $2 . 51^{(31 - 6)} \approx$ 10¹⁰ times dimmer than the faintest object that can be detected by the naked eye!

Worked example

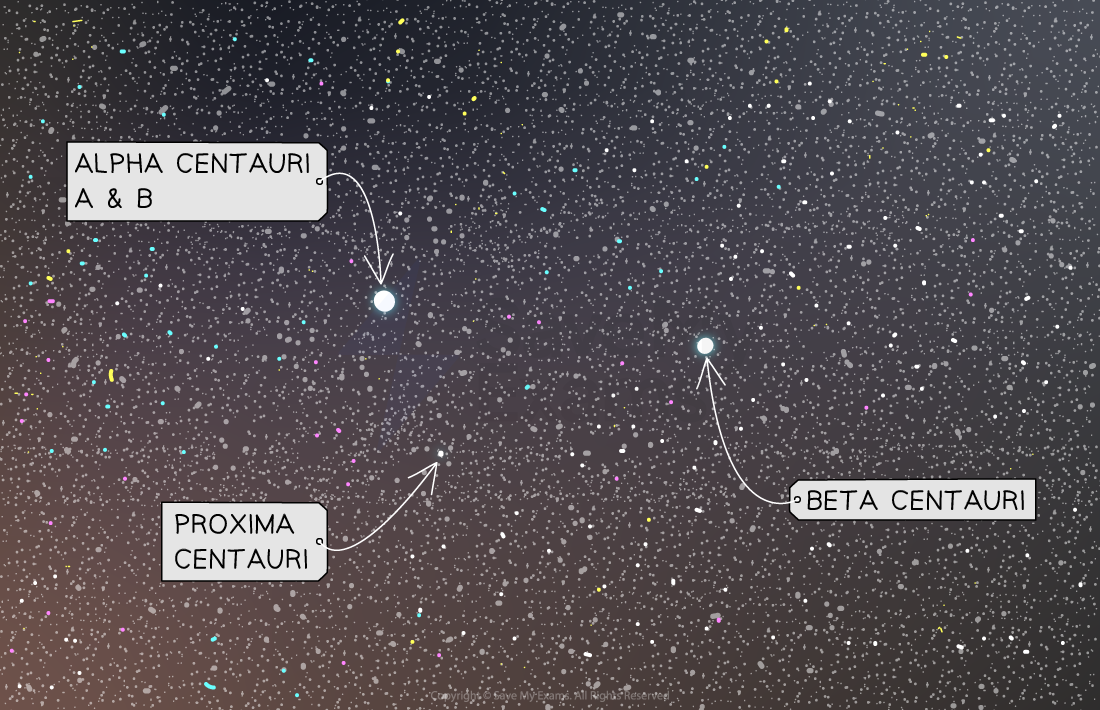
The constellation of Centaurus contains two triple star systems, Alpha Centauri and Beta Centauri.

Alpha Centauri is made up of the binary star pair Alpha Centauri A and B along with Proxima Centauri, the closest star to the Earth after the Sun.

Beta Centauri also contains a binary star pair Beta Centauri Aa and Ab, along with Beta Centauri B.

To the naked eye, some of these stars appear to be a single star. The combined apparent magnitudes are shown in the table.

Star	Apparent magnitude
Alpha Centauri A	−0.27
Alpha Centauri B	−0.27
Proxima Centauri	11.1
Beta Centauri Aa	0.61
Beta Centauri Ab
Beta Centauri B

Compare the stars as seen by a naked-eye observer on Earth. Support your answer with suitable calculations.

Answer:

Step 1: Identify the brightest and dimmest objects

The higher the magnitude, the dimmer the star
- Proxima Centauri has the highest apparent magnitude
- Therefore, Proxima Centauri appears the dimmest

The lower the magnitude, the brighter the star
- The binary pair Alpha Centauri A and B have the lowest apparent magnitude
- Therefore, Alpha Centauri A and B appear the brightest

Step 2: Identify how many stars will be visible to the naked eye

Only two points of light will be visible:
- Alpha Centauri A and B appear as a single star
- All three stars in Beta Centauri appear as a single star

According to the Hipparcos scale, magnitude 6 is the dimmest star that can be observed by the naked eye
- Therefore, Proxima Centauri will not be visible

Step 3: Make comparisons between the intensities of the stars

The ratio of the brightness, or intensities, of two objects is given by

$\frac{I_{A}}{I_{B}} = 2 . 51^{(m_{B} - m_{A})}$

Where object A = Alpha Centauri A and B (appearing as one star), and object B = Beta Centauri
The difference in magnitude between A and B is

$m_{B} - m_{A} = 0.61 - (- 0.27) = 0.88$

The difference in brightness is therefore:

$\frac{I_{A}}{I_{B}} = 2 . 51^{0.88} = 2.25$

This means that Alpha Centauri AB appears 2.25 times brighter than Beta Centauri

9-2-1-we-alpha-beta-and-proxima-centauri

Examiner Tip

The change in intensity equation is not given on your data sheet, so you must remember this.

Brightness & Apparent Magnitude (AQA A Level Physics)

Revision Note