Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesAstrophysicsTelescopesCollecting Power of Telescopes

Collecting Power of Telescopes (AQA A Level Physics)

Revision Note

Katie M

Author

Katie M

Last updated

Collecting Power

  • Telescopes are designed to gather as much light as possible

    • The more light energy a telescope can gather, the brighter the images it will be able to produce

    • This can be measured by a telescope's collecting power

  • The collecting power of a telescope is defined as:

    A measure of the amount of light energy it collects per second

  • This is equivalent to the power per unit area, or intensity of the incident radiation collected

Differences in Collecting Power

9-1-6-collecting-power

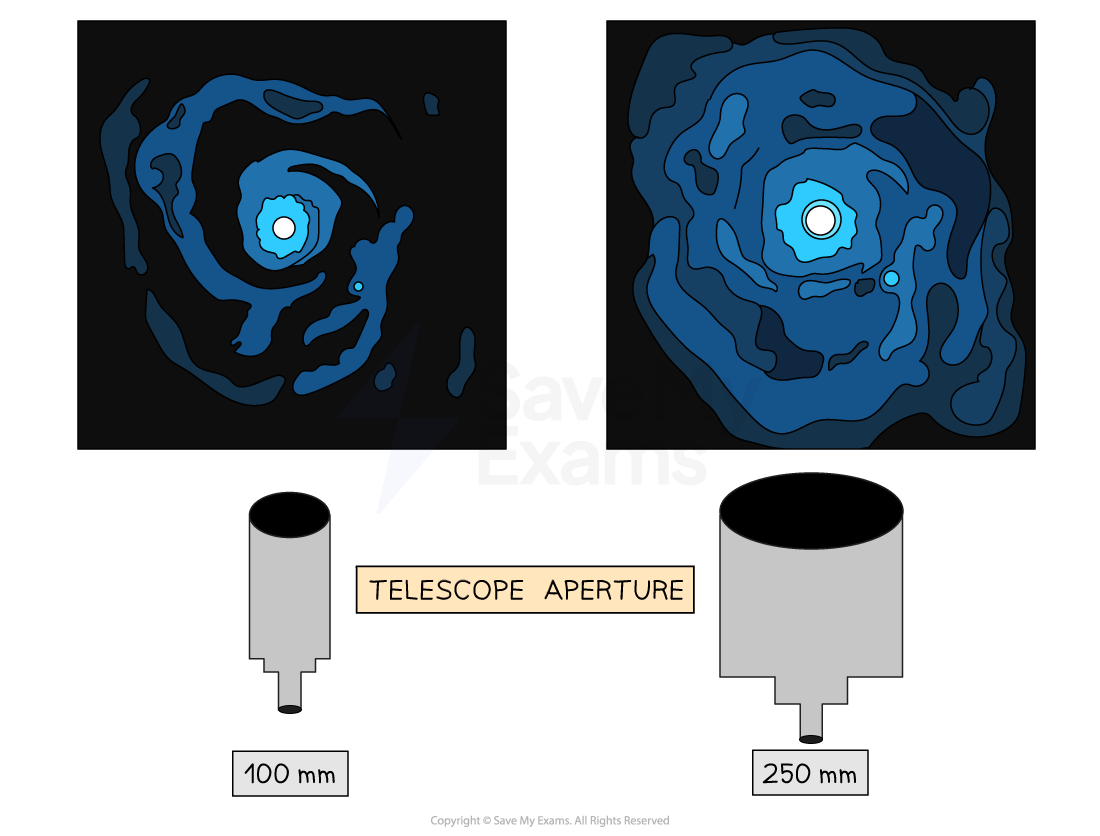
The telescope with the larger aperture is able to produce a brighter image

  • The collecting power of a telescope is directly proportional to the square of the diameter of its objective

c o l l e c t i n g space p o w e r space proportional to space D squared

  • This is because: 

    • Intensity is proportional to surface area 

    • The surface area of a circular object of diameter D is equal to fraction numerator straight pi D to the power of italic 2 over denominator 4 end fraction

  • This means that objects at greater distances can also be seen

    • The intensity of light from a point source decreases inversely with the square of the distance from the inverse square law

Large Diameter Telescopes

  • Larger aperture diameter telescopes are advantageous for two main reasons:

    • They have a greater collecting power so images are brighter

    • They have a greater resolving power so images are clearer

  • The collecting power of two telescopes can be calculated using the ratio

fraction numerator c o l l e c t i n g space p o w e r space o f space t e l e s c o p e space 1 over denominator c o l l e c t i n g space p o w e r space o f space t e l e s c o p e space 2 end fraction space equals space open parentheses D subscript 1 over D subscript 2 close parentheses squared

  • The resolving power of two telescopes operating at the same wavelength can be calculated using the ratio

fraction numerator r e s o l v i n g space p o w e r space o f space t e l e s c o p e space 1 over denominator r e s o l v i n g space p o w e r space o f space t e l e s c o p e space 2 end fraction space equals space theta subscript 1 over theta subscript 2 space equals space fraction numerator begin display style fraction numerator lambda space over denominator D subscript 1 end fraction end style over denominator begin display style lambda over D subscript 2 end style end fraction space equals space D subscript 2 over D subscript 1

Worked Example

The largest refracting telescope still in operation is the Yerkes refractor. The construction of this telescope later paved the way for the Otto Struve reflector to be built. Both telescopes detect optical wavelengths of light.

The table below summarises some of the properties of the two optical telescopes.

Telescope

Type

Objective diameter / cm

Yerkes

refractor

102

Otto-Struve

reflector

208

 Compare the two telescopes in terms of their collecting power and resolving power.

Answer:

Step 1: Compare the collecting power of the telescopes

  • Since collecting power, or intensity of light collected proportional to area proportional to (diameter)2

fraction numerator c o l l e c t i n g space p o w e r space o f space r e f l e c t o r over denominator c o l l e c t i n g space p o w e r space o f space r e f r a c t o r end fraction space equals space open parentheses D subscript r e f l e c t o r end subscript over D subscript r e f r a c t o r end subscript close parentheses squared

fraction numerator c o l l e c t i n g space p o w e r space o f space r e f l e c t o r over denominator c o l l e c t i n g space p o w e r space o f space r e f r a c t o r end fraction space equals space open parentheses 208 over 102 close parentheses squared space equals space 4.16 space almost equal to space 4

  • The collecting power of the Otto-Struve reflector is 4 times greater than the Yerkes refractor, meaning it will produce brighter images

Step 2: Compare the resolving power of the telescopes

  • Resolving power, or minimum angular resolution:  theta space proportional to space 1 over D  (for the same wavelength)

theta subscript r e f l e c t o r end subscript over theta subscript r e f r a c t o r end subscript space equals space D subscript r e f r a c t o r end subscript over D subscript r e f l e c t o r end subscript

theta subscript r e f l e c t o r end subscript over theta subscript r e f r a c t o r end subscript space equals space 102 over 208 space equals space 0.49 space almost equal to space 0.5

  • The Yerkes refractor can resolve detail half as well as the Otto-Struve reflector

  • Therefore, the resolving power of the Otto-Struve reflector is twice as great as the Yerkes refractor, meaning it will produce clearer images

Examiner Tips and Tricks

Remember: the smaller the value of θ, the greater the resolving power

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Resolving Power of TelescopesNext:Radio, IR, UV & X-Ray Telescopes
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.