Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesAstrophysicsTelescopesResolving Power of Telescopes

Resolving Power of Telescopes (AQA A Level Physics)

Revision Note

Katie M

Author

Katie M

Last updated

Minimum Angular Resolution

  • A circular aperture, such as a lens in a telescope, is designed so that a cone of light can enter into a region behind it

    • This allows light to act like a point source once it passes through

  • When two point sources are placed near each other, or viewed from a large distance, they will appear to be a single unresolved source of light

    • For example, two distant car headlights may initially appear as a single point source until the car moves close enough for your eyes to resolve them into two individual headlights

  • Light from any object passing through a circular aperture, including the human eye, will diffract and create interference fringes upon the detector inside

    • The pattern is circular and is an approximate pattern for a circular aperture

  • The large central maximum is called an Airy disc and is twice as wide as the further maxima in the pattern

9-1-5-airy-disc

Diffraction of Light using a Circular Aperture

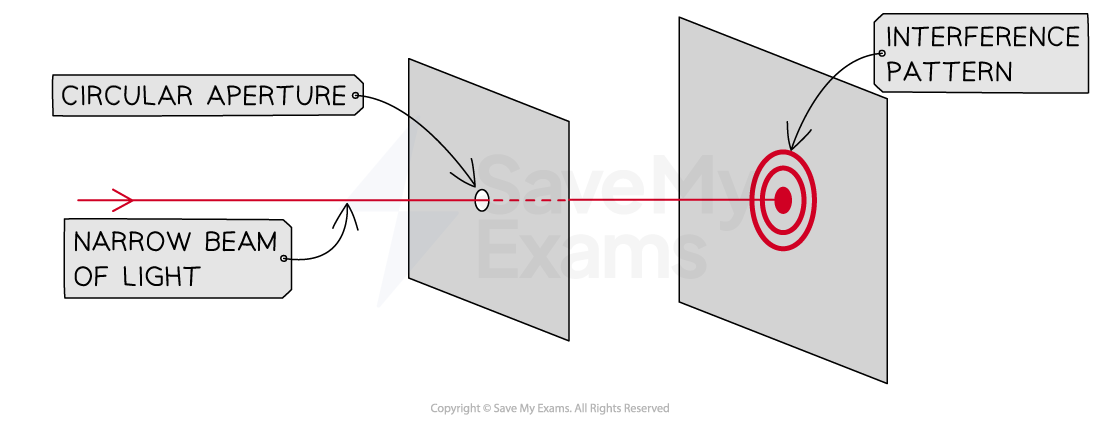
9-1-5-circular-aperature-airy-disc

A circular interference pattern can be seen when light is diffracted through a circular aperture instead of a rectangular slit

  • Diffraction also affects how well a telescope can resolve fine detail

  • The resolving power or minimum angular resolution of a telescope can be determined using the Rayleigh criterion

  • The Rayleigh criterion states that:

    Two sources will be resolved if the central maximum of one diffraction pattern coincides with the first minimum of the other

  • The resolution, or resolving power, of a telescope can be increased by reducing the amount the light diffracts, for example, by:

    • Increasing the diameter of the aperture

    • Operating at a shorter wavelength of light

Visual diffraction pattern

Variation of intensity with separation

9-4-1-visually-unresolved-ib-hl
9-4-1-intensity-resolution-unresolved-ib-hl

A. Two sources that cannot be resolved

 Two sources (red & blue curves) that are too close together appear as one single source (purple curve)

9-4-1-visually-just-resolved-ib-hl
9-4-1-intensity-resolution-rayleigh-criterion-ib-hl

B. Two sources that can only just be resolved, as defined by the Rayleigh Criterion 

 Two sources (red & blue curves) which do not overlap significantly, but just about appear as two sources (purple curve)

C. Two sources that are clearly resolved

 Two sources (red & blue curves) which are far apart enough to appear as two distinct sources (purple curve)

Examiner Tips and Tricks

The terms 'resolution' and 'resolving power' are often both used interchangeably to describe the quality of a telescope in terms of the minimum angular separation it can achieve

For example, saying

  • A telescope has a resolution (or resolving power) of 0.005 degrees

Is the same as saying

  • A telescope can resolve two stars which have an angular separation of at least 0.005 degrees

Remember that the 'Airy disc' is just the central maximum of the interference pattern, not the name of the whole pattern itself.

The Rayleigh Criterion

  • The Rayleigh Criterion can be mathematically described by considering angular separation and single-slit diffraction through a circular aperture

  • Angular separation can be calculated using the equation:

theta space equals space s over d

  • Where:

    • θ = angular separation (rad)

    • s = distance between the two sources (m)

    • d = distance between the sources and the observer (m)

9-4-2-angular-separation-ib-hl

Angular separation, θ, is equal to the separation, s, of two sources divided by the distance, d, between the sources and the observer

  • In single-slit diffraction, minima in the pattern appear at angles given by:

sin space theta space equals space fraction numerator n lambda over denominator D end fraction

  • Where:

    • θ = the angle of diffraction (rad)

    • n = the order of the minimum (1,2,3 etc)

    • λ = the wavelength of the light (m)

    • D = the slit width (m)

Intensity Pattern from a Circular Aperture

9-1-5-diffraction-through-a-circular-aperture

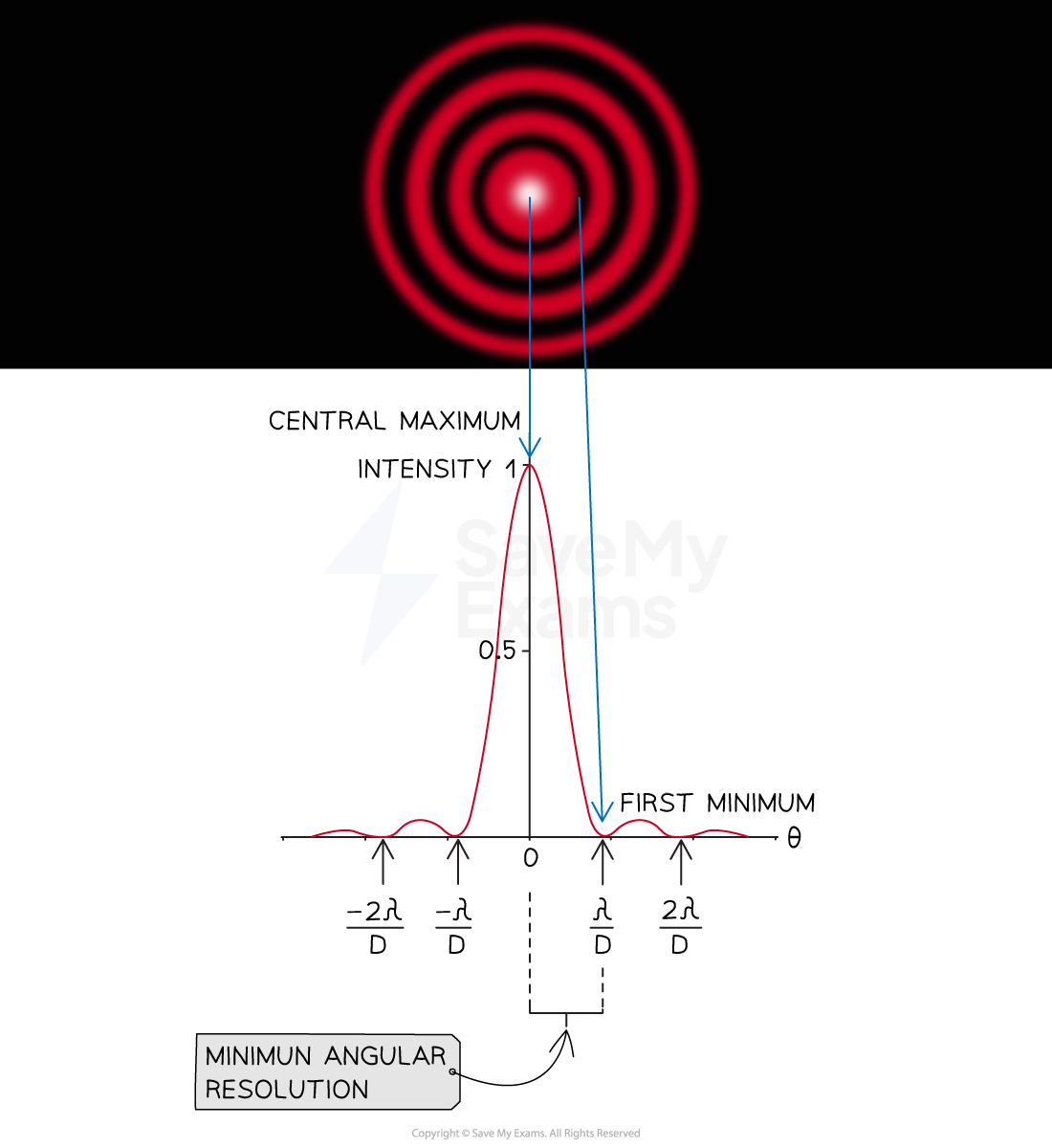
The minimum angular resolution of a telescope can be determined using the angular separation between a source's central maximum and the first minimum

  • For a telescope, the first minimum (when n = 1) occurs when the angle of diffraction is:

sin space theta space equals space lambda over D

  • Using the small-angle approximation open parentheses sin space theta space almost equal to space theta close parentheses, we obtain an expression for the minimum angular resolution of the telescope (The Rayleigh Criterion)

theta space almost equal to space lambda over D

  • Where:

    • θ = minimum angular resolution of the telescope (rad)

    • λ = operating wavelength of the telescope (m)

    • D = diameter of the telescope's aperture (m)

  • The Rayleigh criterion can therefore be written mathematically as follows:

1. Sources are resolvable when

theta space greater than space lambda over D

2. Sources are just resolvable when

theta space almost equal to space lambda over D

3. Sources are not resolvable when

theta space less than space lambda over D

  • For a circular aperture, the value is multiplied by a factor of 1.22

theta space equals fraction numerator space 1.22 lambda over denominator D end fraction

  • This is the same as the expression for two sources that are 'just resolvable' but removes the need for the "approximately equals" (almost equal to) sign

Worked Example

The supermassive black hole at the centre of the Milky Way galaxy is 25,000 light years from the Earth. It has a Schwarzchild radius of 1.2 × 1010 m and emits radio waves at a frequency of 230 GHz.

The Event Horizon Telescope (EHT) is an array of radio telescopes which has the same resolution as a single radio telescope with a diameter of 8000 km.

(a) Calculate the minimum angular separation which could be resolved by the EHT.

 (b) Deduce whether the resolution of the EHT is suitable to obtain a detailed view of the supermassive black hole. Support your answer with a calculation.

 Answer:

Part (a) 

Step 1: List the relevant quantities

  • Frequency of the radio waves, f = 230 GHz = 230 × 109 Hz

  • Speed of light, c = 3 × 108 m s−1

  • Diameter of EHT, D = 8000 km = 8000 × 103 m

Step 2: Write down the equation for the minimum angular separation and substitute in the wave equation 

  • Wave equation: lambda space equals space c over f

  • Minimum angular separation:  theta space equals space lambda over D space equals space fraction numerator c over denominator f D end fraction

Step 3: Calculate the minimum angular separation the EHT can resolve

theta space equals space fraction numerator 3 cross times 10 to the power of 8 over denominator open parentheses 230 cross times 10 to the power of 9 close parentheses cross times open parentheses 8000 cross times 10 cubed close parentheses end fraction = 1.63 × 10−10 rad

  • This means the EHT can obtain a detailed view of objects down to an angular size of 1.63 × 10−10 rad

Part (b)

Step 1: List the relevant quantities

  • Diameter of the black hole, s = 2 × (1.2 × 1010) m = 2.4 × 1010 m

  • Light year, 1 ly = 9.46 × 1015 m (included in the data booklet)

  • Distance to black hole, d = 25 000 ly

Step 2: Write down the equation for angular size

  • Angular size = angle subtended by the black hole (i.e. 2 × Schwarzchild radius): 

s space equals space d theta space space space space space rightwards double arrow space space space space space theta space equals space s over d

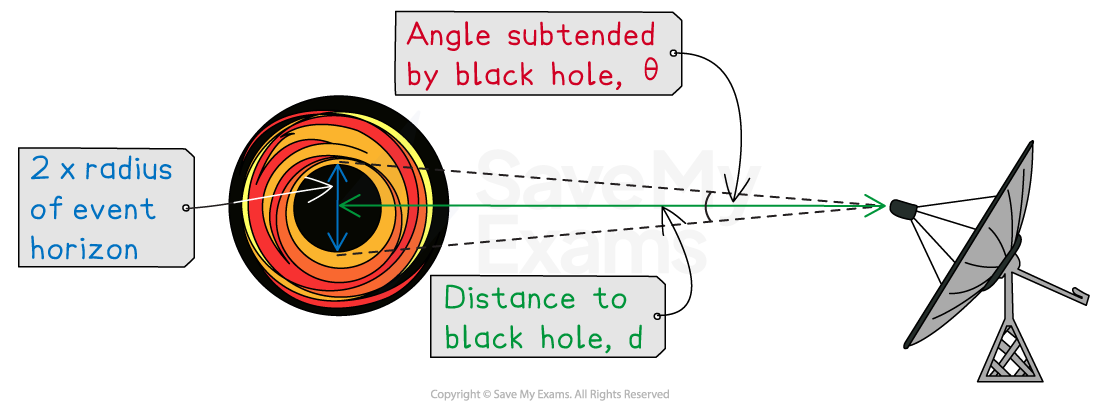
Diagram showing a radio telescope measuring the size of a black hole. Labels: angle θ, distance d, and twice the event horizon radius. Lines and arrows indicate measurements.

Step 3: Carry out a supporting calculation and write a conclusion

You could use...

Method 1:  Calculate the angle subtended by the black hole

  • At a distance of 25 000 ly, the black hole subtends an angular size of:

theta space equals space s over d

theta space equals space fraction numerator 2.4 cross times 10 to the power of 10 over denominator 25 space 000 space cross times space open parentheses 9.46 cross times 10 to the power of 15 close parentheses end fraction = 1.01 × 10−10 rad

  • Compare with the resolution of the EHT:

So, 1.63 × 10−10 rad > 1.01 × 10−10 rad

  • Conclusion:

The angle subtended by the black hole, 1.01 × 10−10 rad, is approximately 1.6 times greater than the limit of the resolution of the EHT, 1.63 × 10−10 rad.

Therefore, it will not be able to suitably resolve detail in an image of the black hole.

The angle of the black hole as viewed from Earth is wider than the angle that the telescope can view. 

Or, you could use...

Method 2:  Calculate the size of an object that could just be resolved at this distance

  • At a distance of 25 000 ly, the smallest object the EHT could resolve in detail is:

s space equals space d theta

s space equals space 25 space 000 space cross times space open parentheses 9.46 cross times 10 to the power of 15 close parentheses space cross times space open parentheses 1.63 cross times 10 to the power of negative 10 end exponent close parentheses = 3.85 × 1010 m

  • Compare with the diameter of the black hole:

So, 3.85 × 1010 m > 8 × 106 m

  • Conclusion: 

The smallest object the EHT could just resolve at this distance, 3.85 × 1010 m, is approximately 1.6 times greater than the diameter of the black hole, 1.2 × 1010 m.

Therefore, it will not be able to suitably resolve detail in an image of the black hole.

The distance between two objects that can be identified as two when viewed from Earth is much greater than the diameter of the black hole. 

Examiner Tips and Tricks

It is better to say that θ is the 'minimum angular resolution' of the telescope instead of 'resolving power', as this implies that θ is a power (in Watts) instead of an angle. However, if you are asked for the resolving power in the exam, it means to calculate θ.

Remember the wavelength and diameter must be in the same units. 

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Reflecting vs Refracting TelescopesNext:Collecting Power of Telescopes
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.