Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesAstrophysicsTelescopesRefracting Telescopes

Refracting Telescopes (AQA A Level Physics)

Revision Note

Katie M

Author

Katie M

Last updated

Ray Diagram for a Refracting Telescope

  • A refracting telescope, or refractor, utilises two converging lenses to project images of distant objects

  • One of the lenses is called an objective lens

    • This lens collects the light from stars and brings it to a focus at its focal length f subscript o 

  • The other lens is called an eyepiece lens

    • This lens is placed at a distance of its focal length f subscript e away from the image and produces parallel rays of light to be analysed

Ray Diagram for a Refractor

9-1-2-ray-diagram-for-a-refractor

Ray diagram of a refracting telescope in normal adjustment showing axial and non-axial rays

  • A simple refractor is usually adjusted so that the final image is at infinity

    • This is known as normal adjustment

  • For a refractor to be in normal adjustment

    • Both lenses must be arranged so that their focal points meet in the same place

    • The focal length of the objective lens must be longer than the focal length of the eyepiece lens, i.e. f subscript o space greater than space f subscript e

  • Note: in the exam, you will be expected to draw this ray diagram with at least 3 non-axial rays - see the worked example below

Worked Example

Draw a ray diagram for an astronomical refracting telescope in normal adjustment.

Your diagram should show the paths of three non-axial rays passing through both lenses.

Label the principal foci of the two lenses.

zQ9lZ_cf_9-1-2-we-refractor-ray-diagram---principal-axis

Answer:

Step 1: Start by drawing and labelling the two lenses

UzlAC1lQ_9-1-2-we-refractor-ray-diagram-step-1

  • If the question does not include a principal axis, make sure to draw this first!

  • You can draw the lenses as lines with arrows or very thin ellipses

Step 2: Mark and label the common principal foci

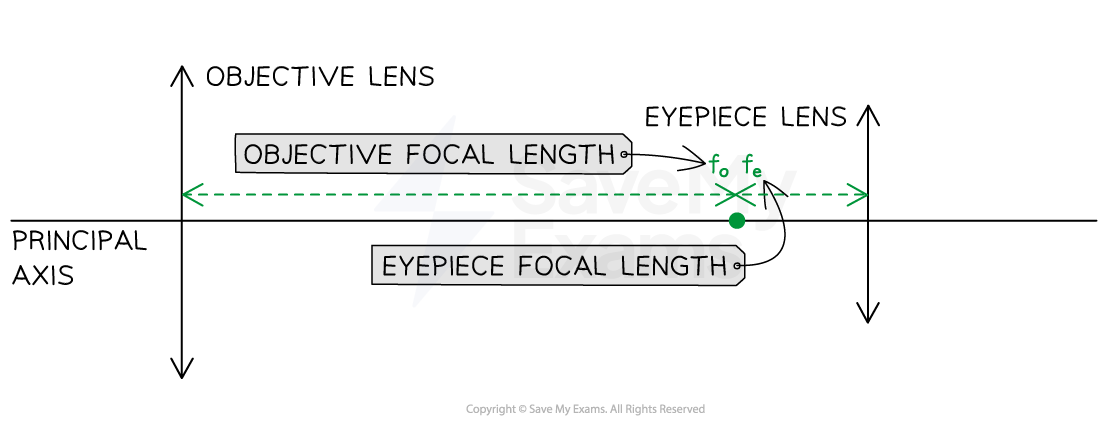
ih-NoNcq_9-1-2-we-refractor-ray-diagram-step-2

  • The objective focal length must be longer than the eyepiece focal length open parentheses f subscript o space greater than space space f subscript e close parentheses

  • You could also mark a single point and label it F 

Step 3: Draw an off-axis ray through the centre of the objective to the eyepiece

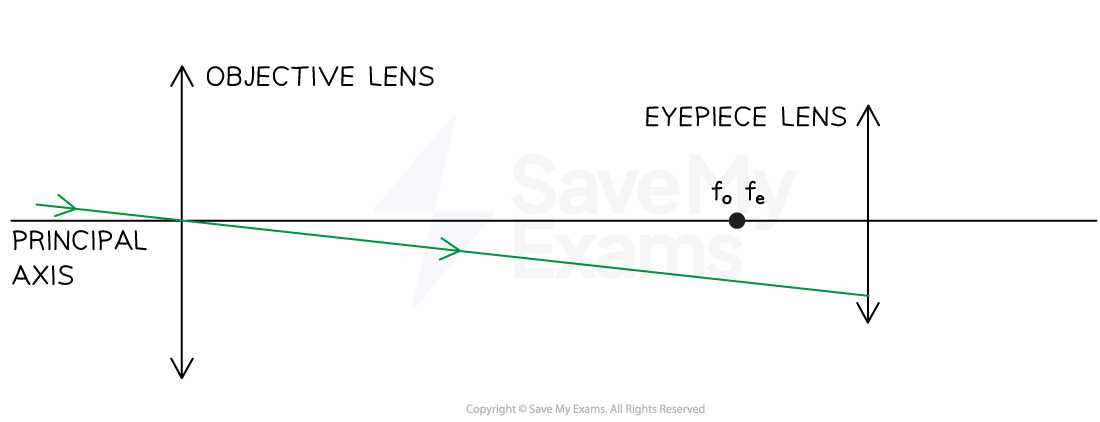
AdyDAE5Z_9-1-2-we-refractor-ray-diagram-step-3

 

  • The rays must be off-axis (non-axial), meaning drawn at an angle to the principal axis

Step 4: Draw an arrow to show the intermediate image from the common principal foci to this ray

mQbFzuzv_9-1-2-we-refractor-ray-diagram-step-4

  • You don't have to do this step, but it will help the examiner to clearly see your working

Step 5: Draw a construction line from the end of the intermediate image through the centre of the eyepiece

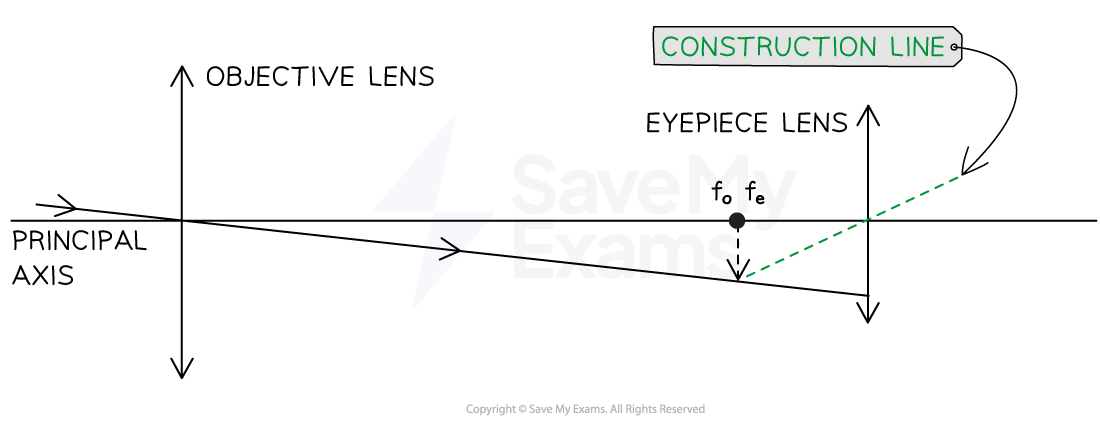
aIKuWOLZ_9-1-2-we-refractor-ray-diagram-step-5

  • You don't have to do this either, but it will help the examiner to clearly see your working

Step 6: Draw two rays to the eyepiece, crossing at where the focal lengths meet

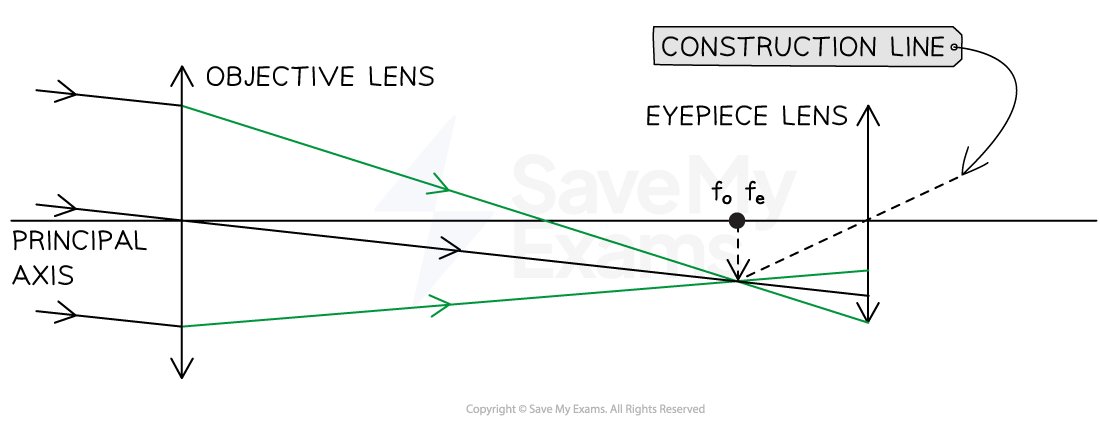
BYxxw2E6_9-1-2-we-refractor-ray-diagram-step-7

Step 7: Draw the continuation of the three rays from the eyepiece, parallel to the construction line

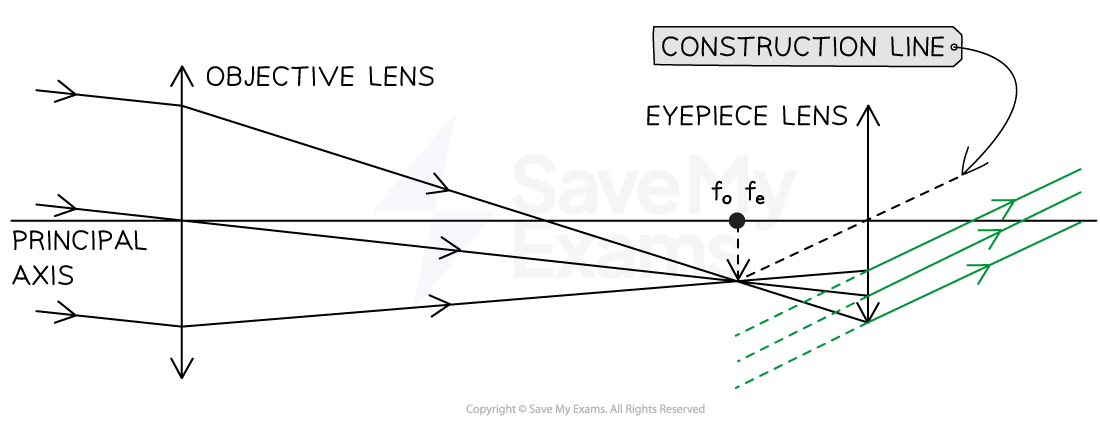
Kv1YH0Qd_9-1-2-we-refractor-ray-diagram-step-8

Step 8: Check your final image and make sure everything is included to gain the marks

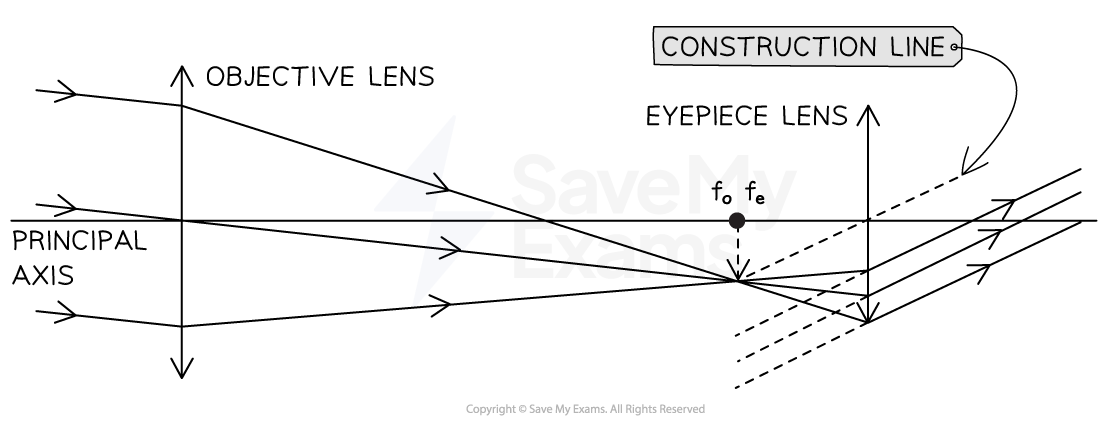
xIgeLG44_9-1-2-we-refractor-ray-diagram-final

  • For a three-mark question, examiners will be looking for:

    • Both focal points are marked and labelled at the same point on the principal axis with f subscript o space greater than space f subscript e

    • Three off-axis rays drawn through the objective lens

    • Three rays drawn through the eyepiece lens parallel to a construction line

Examiner Tips and Tricks

It is important that you get lots of practice drawing this diagram, it's a common exam question, and examiners can be extremely meticulous when it comes to marking them 

Make sure to avoid these common problems when drawing the diagram:

  • Drawing axial rays (parallel to the principal axis) rather than non-axial rays (at an angle to the principal axis)

  • Bending the central ray at the objective lens

  • Bending the rays at the intermediate image (i.e. at f subscript o, f subscript e)

  • Not drawing the rays parallel to each other, or the construction line, at the eyepiece lens

  • Labelling the principal foci where the rays cross, rather than on the principal axis

Angular Magnification

  • The angle, in radians, subtended by an object of height h, at a distance d away is given by:

theta space equals space h over d

  • This is also known as the angular size of an object

  • Note: this is the angle between the rays seen at the extremities of the object to the eyes or telescope lens

Angular Size of the Moon

SnFUjEaC_9-1-2-angular-size-of-the-moon

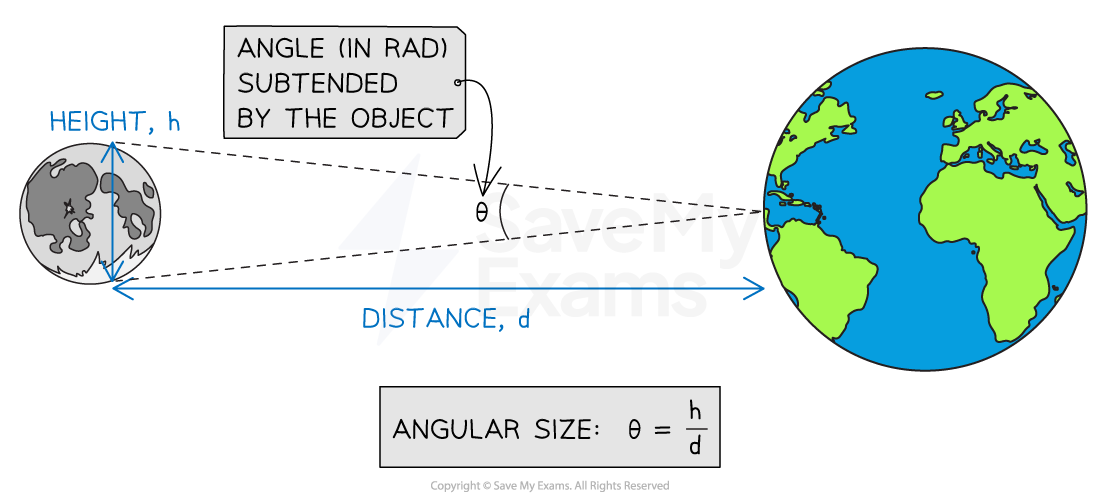
How to calculate the angle subtended by an astronomical object

  • For astronomical objects that are very distant, essentially at infinity, it isn't easy to directly measure their size or the distance to them

  • Therefore, it makes more sense to use angular magnification, which is defined as:

 M space equals space fraction numerator a n g l e space s u b t e n d e d space b y space i m a g e space a t space e y e over denominator a n g l e space s u b t e n d e d space b y space o b j e c t space a t space u n a i d e d space e y e end fraction space equals space beta over alpha

  • Like magnification, angular magnification is a ratio and has no units

Angles Subtended by the Object & the Image

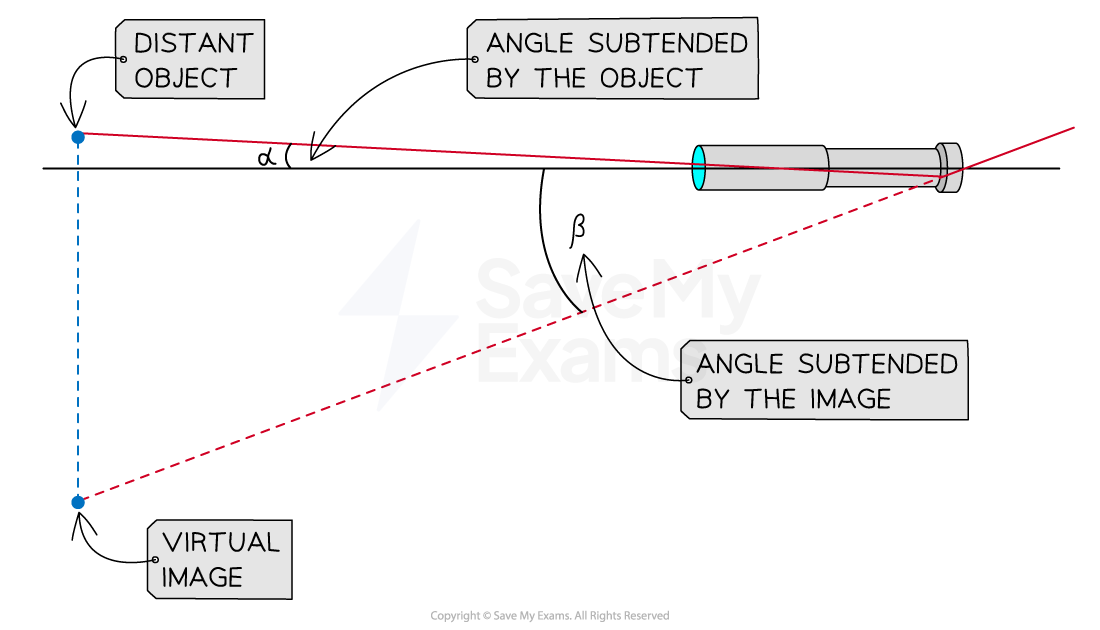
ahvy~vYb_9-1-2-angular-magnification-in-a-refractor

The angle subtended by an astronomical object and the angle subtended by the image produced by the telescope

  • Telescopes magnify the angular size of distant objects, this means that: 

    • The telescope produces an image which subtends a larger angle than the object 

    • When viewed by the naked eye, the angle subtended by the object alpha is much less than the angle subtended by the image beta when viewed through a telescope

Angular Magnification of a Refractor

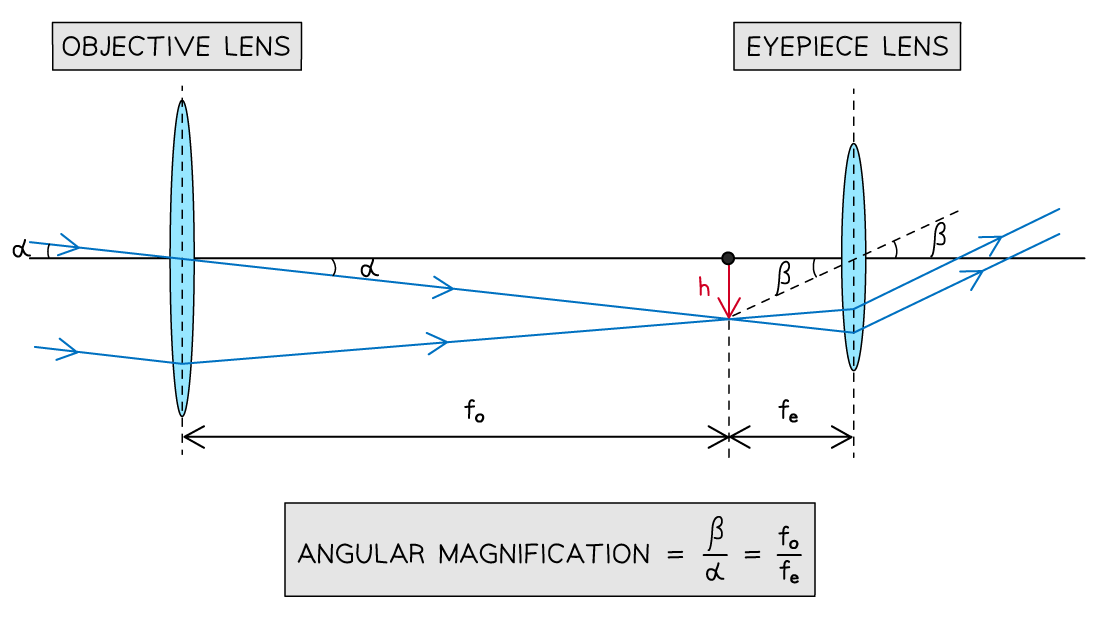
u79ww3df_9-1-2-angular-magnification-normal-adjustment

How to determine the angular magnification of a refracting telescope in normal adjustment

  • When looking at the ray diagram of a refractor in normal adjustment, the rays of light inside the telescope can be seen to form similar triangles

  • The angle subtended by the object open parentheses alpha close parentheses can be described as:

tan space alpha space equals space h over f subscript o space space space space space rightwards double arrow space space space space space alpha space equals space h over f subscript o

  • The angle subtended by the image open parentheses beta close parentheses can be described as:

tan space beta space equals space h over f subscript e space space space space space rightwards double arrow space space space space space beta space equals space h over f subscript e

  • Where:

    • h = the height of the image (m)

    • f subscript o = focal length of the objective lens (m)

    • f subscript e = focal length of the eyepiece lens (m)

    • tan space theta space almost equal to space theta when the angle is very small (rad)

  • Combining these equations leads to the following expression for angular magnification:

M space equals space beta over alpha space equals space f subscript o over f subscript e

  • This equation tells us that to achieve greater magnifications:

    • longer objective focal lengths open parentheses f subscript o close parentheses and shorter eyepiece focal lengths open parentheses f subscript e close parentheses are required

    • refractors must be very long, as the length is equal to space f subscript o space plus space f subscript e

Worked Example

A student is looking for suitable lenses to use in a simple refracting astronomical telescope. 

The student sets out to measure the focal length of a converging lens by placing an object and screen at a fixed distance of 300 cm apart.

A sharp image is observed on the screen when the lens is placed between the object and the screen at a distance of 207 cm from the object.

(a) Calculate the focal length of the lens.

(b) State whether the lens formed the eyepiece or objective, giving reasons for your answer.

Answer:

Part (a)

Step 1: Sketch a quick diagram to visualise the scenario

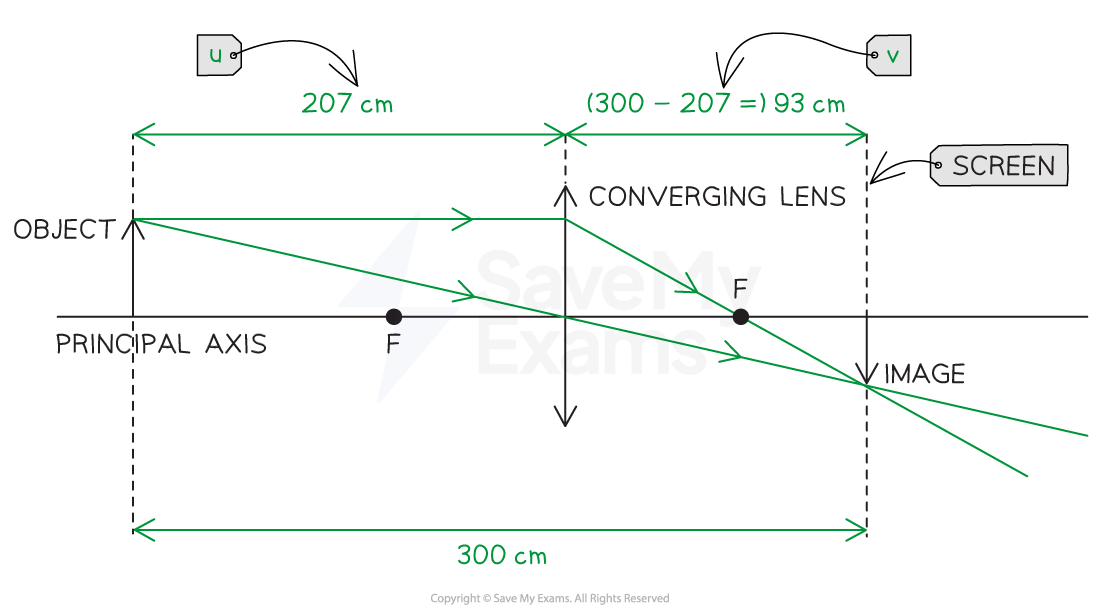
G9hpIyHV_9-1-2-we-angular-magnification

Step 2: Write down the lens equation

lens equation:  1 over f space equals space 1 over u space plus space 1 over v

  • Where u = 207 cm and v = 93 cm

Step 3: Calculate the focal length of the lens

1 over f space equals space 1 over 207 space plus space 1 over 93

f space equals space open parentheses 1 over 207 space plus space 1 over 93 close parentheses to the power of negative 1 end exponent space equals space 64 space cm

Part (b)

You could either argue...

  • The eyepiece forms a virtual, inverted, magnified image

  • The objective lens forms a real, inverted, diminished image of a distant object very near the focal point of the eyepiece

  • The image formed by the lens in (a) is real, inverted, and diminished

  • Therefore, the lens must be an objective lens

Or, you could argue...

  • In a refracting telescope, angular magnification is given by:  M space equals space f subscript o over f subscript e

  • Hence, the eyepiece must have a shorter focal length and the objective must have a longer focal length:  f subscript o space greater than space space f subscript e

  • For the best possible magnification, the image due to the objective lens, which acts as the object for the eyepiece lens, must be located at the focal point of the eyepiece

  • Hence, the two lenses must be separated by a distance f subscript o space plus space space f subscript e (i.e. the telescope length)

  • Therefore, the lens must be an objective lens

Worked Example

An astronomical refracting telescope which is 1.23 m long and has an angular magnification of 200 is used to observe Neptune at its closest approach to Earth.

  • distance from Earth to Neptune at closest approach = 4.3 × 109 km

  • diameter of Neptune = 4.9 × 104 km

(a) Calculate the focal lengths of the objective lens and eyepiece lens.

(b) Calculate the angle subtended by the image of Neptune when viewed through this telescope.

Answer:

Part (a)

Step 1: List the relevant equations and known quantities

Telescope length:  f subscript o space plus space space f subscript e space equals space 1.23 space straight m

Angular magnification:  M space equals space f subscript o over f subscript e space equals space 200

Step 2: Write an expression for one of the focal lengths in terms of the other

f subscript o space equals space 200 space f subscript e

200 space f subscript e plus space space f subscript e space equals space 1.23 space straight m

201 space f subscript e space equals space 1.23 space straight m

Step 3: Solve to determine the focal lengths of the lens

  • Focal length of the eyepiece:  f subscript e space equals space fraction numerator 1.23 over denominator 201 end fraction space equals space 6.1 space cross times space 10 to the power of negative 3 end exponent space straight m space almost equal to space 0.01 space straight m

  • Focal length of the objective:  f subscript o space equals space 200 space cross times space open parentheses 6.1 cross times 10 to the power of negative 3 end exponent close parentheses space equals space 1.22 space straight m

Part (b)

Step 1: Recall the equations for angular size and angular magnification

Angular size: theta space equals fraction numerator space h over denominator d end fraction

  • Where diameter, h = 4.9 × 104 km and distance, d = 4.3 × 109 km

Angular magnification:  M space equals space beta over alpha

  • Where α = angle subtended by Neptune at unaided eye and β = angle subtended by the image of Neptune at eye

Step 2: Determine the angle subtended by Neptune at unaided eye

theta space equals space fraction numerator 4.9 cross times 10 to the power of 4 over denominator 4.3 cross times 10 to the power of 9 end fraction space equals space 1.14 space cross times space 10 to the power of negative 5 end exponent space rad

  • The angle subtended by Neptune with the unaided eye:  α = 1.14 × 10–5 rad

Step 3: Determine the angle subtended by the image of Neptune at the eyepiece

M space equals space beta over alpha space space space space space rightwards double arrow space space space space space beta space equals space alpha M

beta space equals space open parentheses 1.14 cross times 10 to the power of negative 5 end exponent close parentheses space cross times space 200 space equals space 2.28 space cross times space 10 to the power of negative 3 end exponent space rad

  • Angle subtended by the image of Neptune at eyepiece:  β = 2.28 × 10–3 rad

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Lenses & Ray Diagrams for TelescopesNext:Reflecting Telescopes
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.