Lenses & Ray Diagrams for Telescopes (AQA A Level Physics)

• A lens is a piece of equipment that forms an image by refracting light
• There are two types of lenses: 
  • A convex, or converging lens
  • A concave, or diverging lens
• Note: in the Astrophysics module, only converging lenses will be discussed

• In a converging lens, parallel rays of light are brought to a focus along the principal axis
  • This point is called the focal point

• The distance from the centre of the lens to the focal point is called the focal length
  • This length depends on how curved, or how thick, the lens is
  • The more curved (thicker) the lens, the shorter the focal length
  • The shorter the focal length, the more powerful the lens

The focal length is shorter in a lens that is thicker and more curved. This makes for a more powerful lens

Real & Virtual Images

• Images produced by lenses can be either real or virtual

Real image	Virtual image
light converges towards a focal point	light diverges away from a focal point
always inverted	always upright
can be projected onto a screen	cannot be projected onto a screen
intersection of two solid lines	intersection of two dashed lines (or a dashed and a solid line)
example: image from a projector onto a screen	example: image in a mirror

Constructing Ray Diagrams

• When constructing ray diagrams of refractors, it is generally assumed that the lenses used are very thin
  • This simplifies the situation by reducing the amount the incident rays of light refract

• As a result, the three main rules for constructing ray diagrams are as follows:

1. Rays passing through the principal axis will pass through the optical centre of the lens undeviated

2. Rays that are parallel to the principal axis will be refracted and pass through the focal point f

3. Rays passing through the focal point f will emerge parallel to the principal axis

Image Formation by a Converging Lens

• Images formed by lenses can be described by their
  • Nature: Real or virtual
  • Orientation: Inverted or upright (compared to the object)
  • Size: Magnified (larger), diminished (smaller), or the same size (compared to the object)

Drawing ray diagrams of real images

• For an object placed at a distance greater than 2 focal lengths...

• The image that forms will have the following properties:

The image forms...	between f and 2f
The nature of the image is...	real
The orientation of the image is...	inverted
The size of the image is...	diminished

 

• For an object placed at a distance equal to 2 focal lengths...

• The image that forms will have the following properties:

The image forms...	at 2f
The nature of the image is...	real
The orientation of the image is...	inverted
The size of the image is...	the same

 

• For an object placed at a distance between 1 and 2 focal lengths

• The image that forms will have the following properties:

The image forms...	beyond 2f
The nature of the image is...	real
The orientation of the image is...	inverted
The size of the image is...	magnified

 

Drawing ray diagrams of virtual images

• For an object placed at a distance less than the focal length (i.e. a magnifying glass):

• The image that forms will have the following properties:

The image forms...	at 2f (on the same side as the object)
The nature of the image is...	virtual
The orientation of the image is...	upright
The size of the image is...	magnified

The Lens Equation

• The lens equation relates the focal length of a lens to the distances between the lens and the image and the object

• Where:
  • f = focal length (m)
  • v = distance of the image from lens (m)
  • u = distance of the object from lens (m)

Lens Equation for a Real Image

All values are positive for a real image

• This equation only works for thin converging (or diverging) lenses
  • If the image is real, the value of v is positive 
  • If the image is virtual, the value of v is negative

Lens Equation for a Virtual Image

A virtual image forms on the same side as the object making the value of v negative

Magnification as a Ratio of Heights

• Magnification, M, is the ratio of the image height to the object height

• Where:
  • = magnification
  •  = image height (m)
  •  = object height (m)

Magnification as a Ratio of Distances

• A diagram of an object and its real image will produce similar triangles
• Therefore, magnification can be determined by comparing the distances from the lens to the object and the image

Magnification Ray Diagram for a Real Image

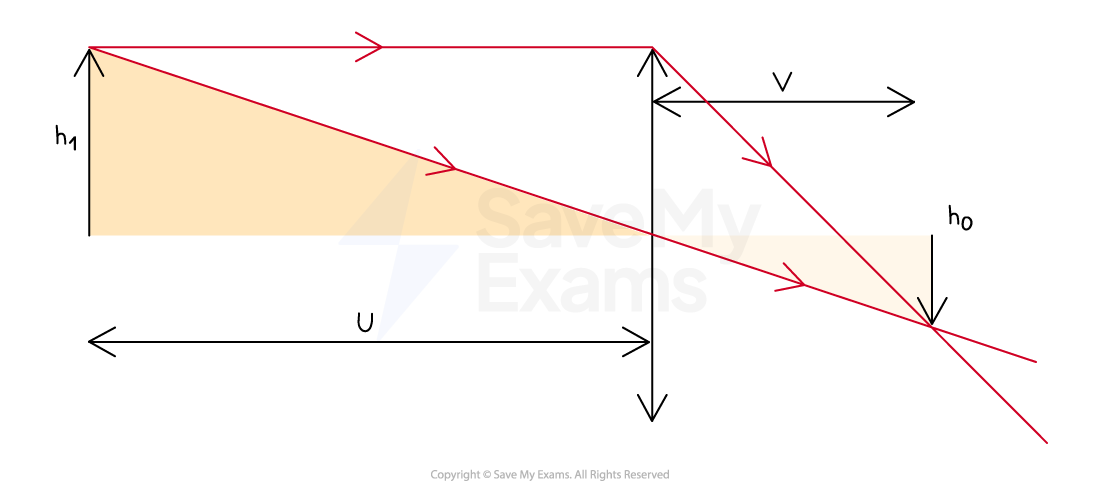
Magnification for a real image can be derived using similar triangles

• This also works for virtual images

Magnification Ray Diagram for a Virtual Image

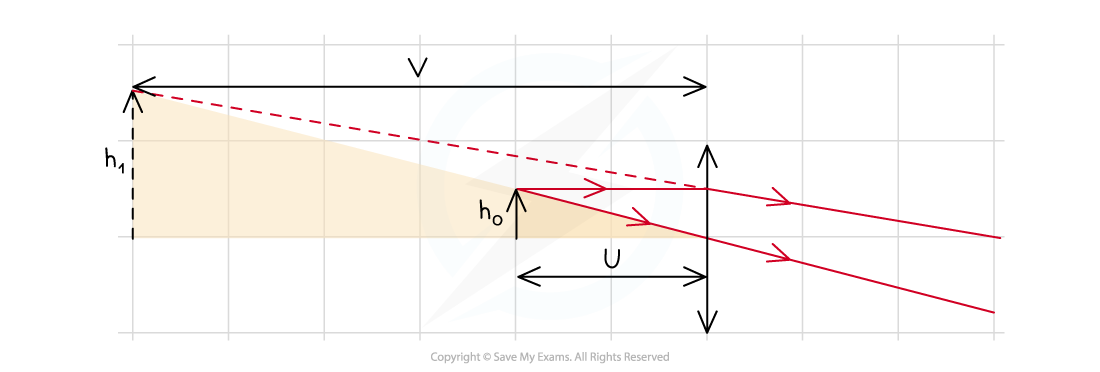
Magnification for a virtual image can also be derived using similar triangles

• As magnification can be described using the ratio of the two opposite sides and , the same ratio must apply to the two adjacent sides and

• Therefore, magnification can also be written as:

 

• Where:
  • = magnification
  • = distance from lens to image (m)
  • = distance from lens to object (m)

• Since magnification is a ratio, it has no units