Mass Difference & Binding Energy (AQA A Level Physics)

Revision Note

Test yourself

Author

Katie M

Last updated

8 November 2024

Mass Difference & Binding Energy

Experiments into nuclear structure have found that the total mass of a nucleus is less than the sum of the masses of its constituent nucleons
This difference in mass is known as the mass defect
Mass defect is defined as:
The difference between an atom's mass and the sum of the masses of its protons and neutrons
The mass defect Δm of a nucleus can be calculated using:

Δm = Zm_p + (A – Z)m_n – m_total

Where:
- Z = proton number
- A = nucleon number
- m_p = mass of a proton (kg)
- m_n = mass of a neutron (kg)
- m_total = measured mass of the nucleus (kg)

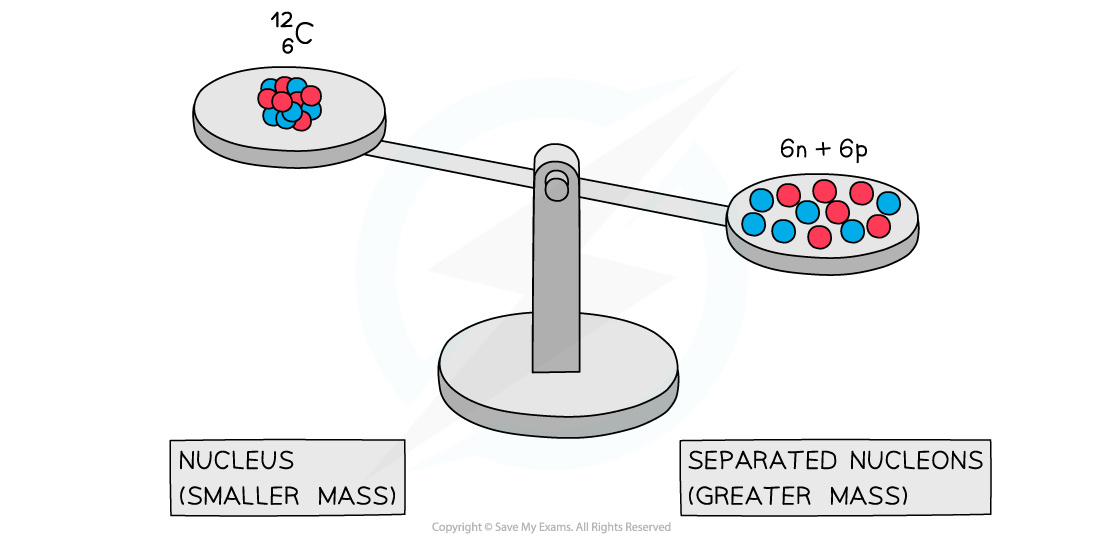
Binding Energy, downloadable AS & A Level Physics revision notes

A system of separated nucleons has a greater mass than a system of bound nucleons

Due to the equivalence of mass and energy, this decrease in mass implies that energy is released in the process
Since nuclei are made up of neutrons and protons, there are forces of repulsion between the positive protons
- Therefore, it takes energy, ie. the binding energy, to hold nucleons together as a nucleus

Binding energy is defined as:
The amount of energy required to separate a nucleus into its constituent protons and neutrons
Energy and mass are proportional, so, the total energy of a nucleus is less than the sum of the energies of its constituent nucleons
The formation of a nucleus from a system of isolated protons and neutrons is, therefore, an exothermic reaction - meaning that it releases energy
This can be calculated using the equation:

E = Δmc²

In a typical nucleus, binding energies are usually measured in MeV
- This is considerably larger than the few eV associated with the binding energy of electrons in the atom
Nuclear reactions involve changes in the nuclear binding energy whereas chemical reactions involve changes in the electron binding energy
- This is why nuclear reactions produce much more energy than chemical reactions

Worked Example

Calculate the binding energy per nucleon, in MeV, for the radioactive isotope potassium-40 (₁₉K).

Nuclear mass of potassium-40 = 39.953 548 u

Mass of one neutron = 1.008 665 u

Mass of one proton = 1.007 276 u

Answer:

Step 1: Identify the number of protons and neutrons in potassium-40

Proton number, Z = 19
Neutron number, N = 40 – 19 = 21

Step 2: Calculate the mass defect, Δm

Proton mass, m_p = 1.007 276 u
Neutron mass, m_n = 1.008 665 u
Mass of K-40, m_total = 39.953 548 u

Δm = Zm_p + Nm_n – m_total

Δm = (19 × 1.007276) + (21 × 1.008665) – 39.953 548

Δm = 0.36666 u

Step 3: Convert from u to kg

1 u = 1.661 × 10^–27 kg

Δm = 0.36666 × (1.661 × 10^–27) = 6.090 × 10^–28 kg

Step 4: Write down the equation for mass-energy equivalence

E = Δmc²

Where c = speed of light

Step 5: Calculate the binding energy, E

E = 6.090 × 10^–28 × (3.0 × 10⁸)² = 5.5 × 10^–11 J

Step 6: Determine the binding energy per nucleon and convert J to MeV

Take the binding energy and divide it by the number of nucleons
1 MeV = 1.6 × 10^–13 J

Examiner Tips and Tricks

The terms binding energy and mass defect can cause students confusion, so be careful when using them in your explanations.

Avoid describing the binding energy as the energy stored in the nucleus – this is not correct – it is energy that must be put into the nucleus to separate all the nucleons.

The same goes for the term mass defect, make sure to only use this when all the nucleons are separated and not to describe the decrease in mass which occurs during radioactive decay.

Atomic Mass Unit (u)

The unified atomic mass unit (u) is roughly equal to the mass of one proton or neutron:
- 1 u = 1.66 × 10⁻²⁷ kg
It is sometimes abbreviated to a.m.u
This value will be given on your data sheet in the exam
The a.m.u is commonly used in nuclear physics to express the mass of subatomic particles. It is defined as
The mass of exactly one-twelfth of an atom of carbon-12
Therefore, one atom of carbon-12 has a mass of exactly 12 u
Since mass and energy are interchangeable, the a.m.u can also be expressed in MeV
- 1 u is equivalent to 931.5 MeV

Table of common particles with mass in a.m.u

The mass of an atom in a.m.u is roughly equal to the sum of its protons and neutrons (nucleon number)
- For example, the mass of Uranium-235 is roughly equal to 235u
A.m.u might be quoted in kg or MeV since mass and energy are equivalent via E = mc²
- MeV is a unit of energy whilst kg is a unit of mass