Nuclear Fusion & Fission (AQA A Level Physics)

Nuclear Fusion & Fission

Nuclear Fusion

• Fusion is defined as:

  The fusing together of two small nuclei to produce a larger nucleus

• Low mass nuclei (such as hydrogen and helium) can undergo fusion and release energy

• When two protons fuse, the element deuterium is produced

• In the centre of stars, the deuterium combines with a tritium nucleus to form a helium nucleus, plus the release of energy, which provides fuel for the star to continue burning

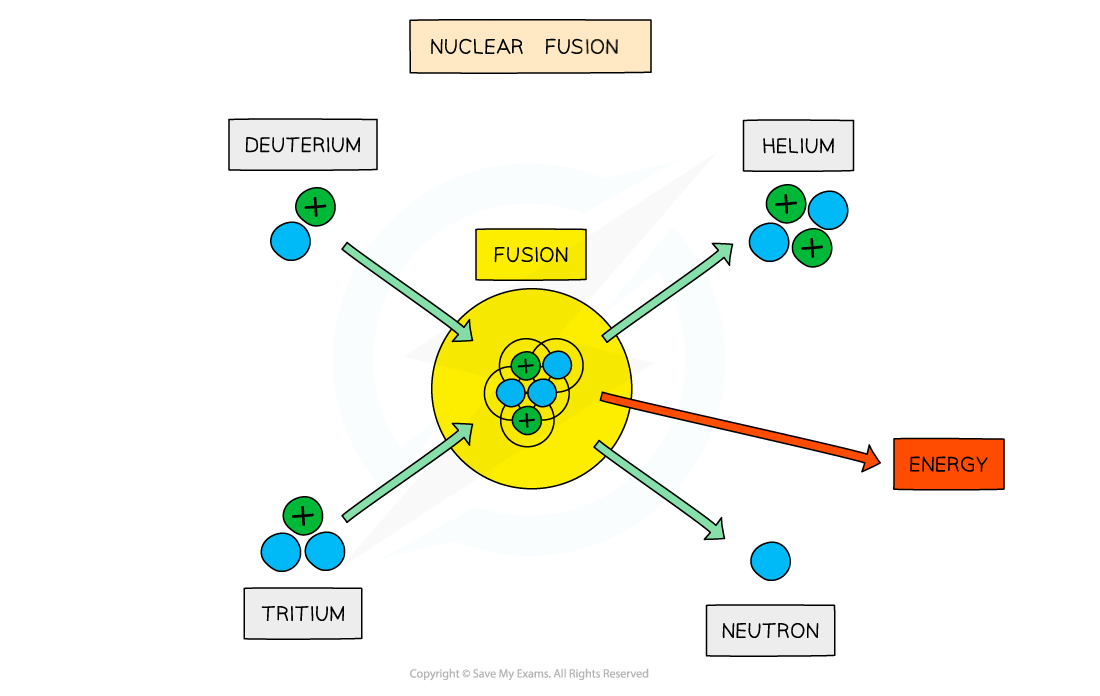
The fusion of deuterium and tritium to form helium with the release of energy

• For two nuclei to fuse, both nuclei must have high kinetic energy

• This is because nuclei must be able to get close enough to fuse

  • However, two forces acting within the nuclei make this difficult to achieve

• Electrostatic Repulsion 

  • Protons inside the nuclei are positively charged, which means that they electrostatically repel one another

• Strong Nuclear Force

  • The strong nuclear force, which binds nucleons together, acts at very short distances within nuclei

  • Therefore, nuclei must get very close together for the strong nuclear force to take effect

• It takes a great deal of energy to overcome the electrostatic force, hence fusion can only be achieved in an extremely hot environment, such as the core of a star

Nuclear Fission

• Fission is defined as:

  The splitting of a large atomic nucleus into smaller nuclei

• High mass nuclei (such as uranium) can undergo fission and release energy

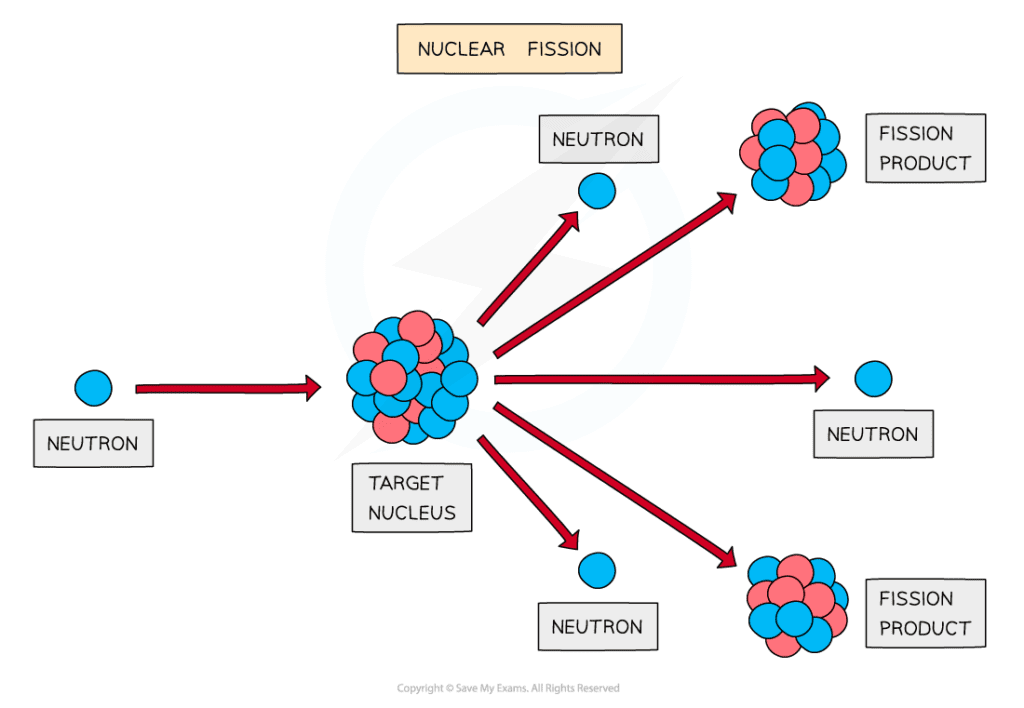
The fission of a target nucleus, such as uranium, to produce smaller daughter nuclei with the release of energy

• Fission must first be induced by firing neutrons at a nucleus

  • When the nucleus is struck by a neutron, it splits into two, or more, daughter nuclei

  • During fission, neutrons are ejected from the nucleus, which in turn, can collide with other nuclei which triggers a cascade effect

  • This leads to a chain reaction which lasts until all of the material has undergone fission, or the reaction is halted by a moderator

• Nuclear fission is the process which produces energy in nuclear power stations, where it is well controlled

• When nuclear fission is not controlled, the chain reaction can cascade to produce the effects of a nuclear bomb

Calculating Energy Released in Nuclear Reactions

• The binding energy is equal to the amount of energy released in forming the nucleus, and can be calculated using:

E = (Δm)c²

• Where:

  • E = Binding energy released (J)

  • Δm = mass defect (kg)

  • c = speed of light (m s^-1)

• The daughter nuclei produced as a result of both fission and fusion have a higher binding energy per nucleon than the parent nuclei

• Therefore, energy is released as a result of the mass difference between the parent nuclei and the daughter nuclei