Nuclear Density (AQA A Level Physics): Revision Note

Constant Density of Nuclear Material

• Assuming that the nucleus is spherical, its volume is equal to:

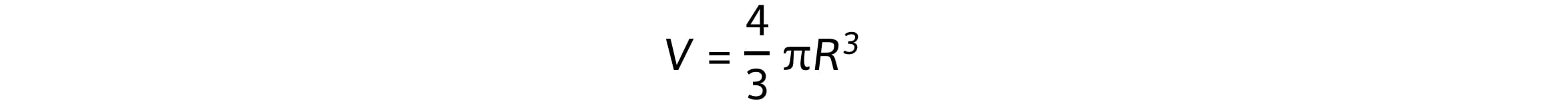
• Where R is the nuclear radius, which is related to mass number, A, by the equation:

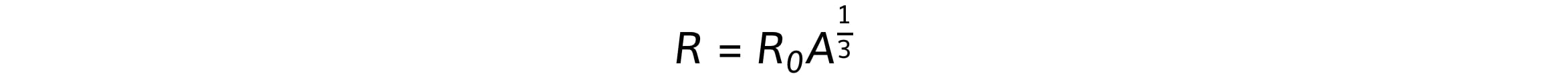
• Where R₀ is a constant of proportionality

• Combining these equations gives:

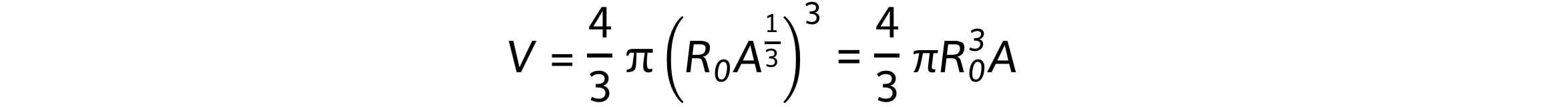
• Therefore, the nuclear volume, V, is proportional to the mass of the nucleus, A

• Mass (m), volume (V), and density (ρ) are related by the equation:

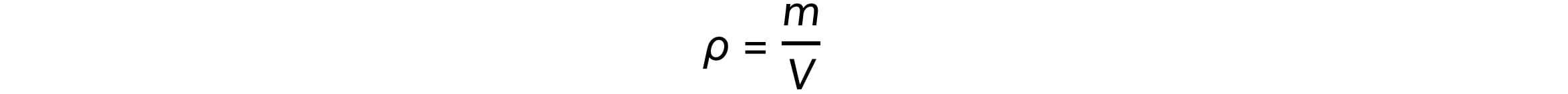
• The mass, m, of a nucleus is equal to:

m = Au

• Where:

  • A = the mass number

  • u = atomic mass unit

• Using the equations for mass and volume, nuclear density is equal to:

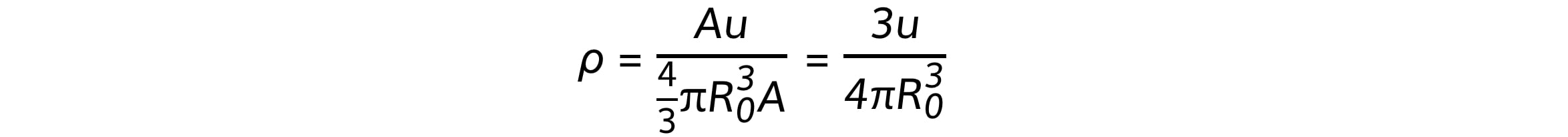
• Since the mass number A cancels out, the remaining quantities in the equation are all constant

• Therefore, this shows the density of the nucleus is:

  • Constant

  • Independent of the radius

• The fact that nuclear density is constant shows that nucleons are evenly separated throughout the nucleus regardless of their size

Nuclear Density

• Using the equation derived above, the density of the nucleus can be calculated:

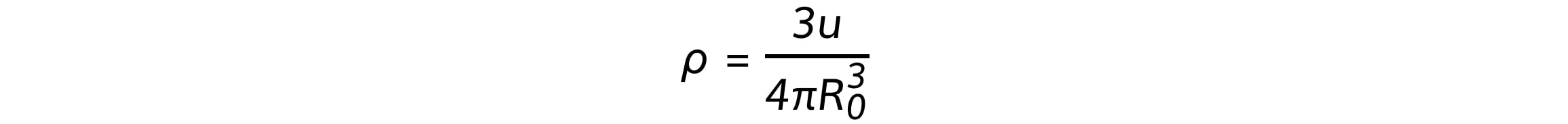
• Where:

  • Atomic mass unit, u = 1.661 × 10^–27 kg

  • Constant of proportionality, R₀ = 1.05 × 10^–15 m

• Substituting the values gives a density of:

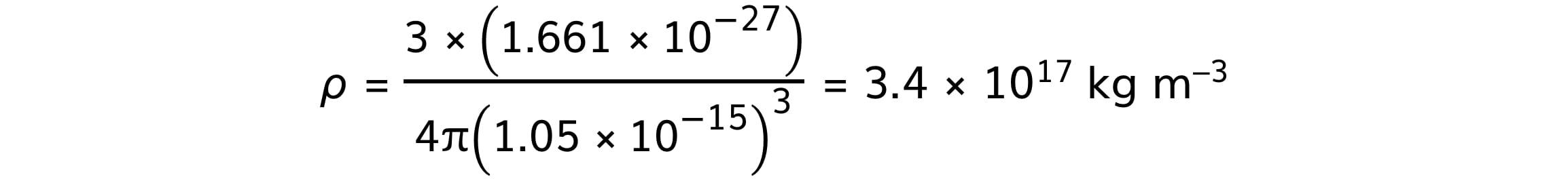
• The accuracy of nuclear density depends on the accuracy of the constant R₀, as a guide nuclear density should always be of the order 10¹⁷ kg m^–3

• Nuclear density is significantly larger than atomic density, this suggests:

  • The majority of the atom’s mass is contained in the nucleus

  • The nucleus is very small compared to the atom

  • Atoms must be predominantly empty space