Nuclear Radius Equation (AQA A Level Physics)

• The radius of some nuclei are shown in the table below:

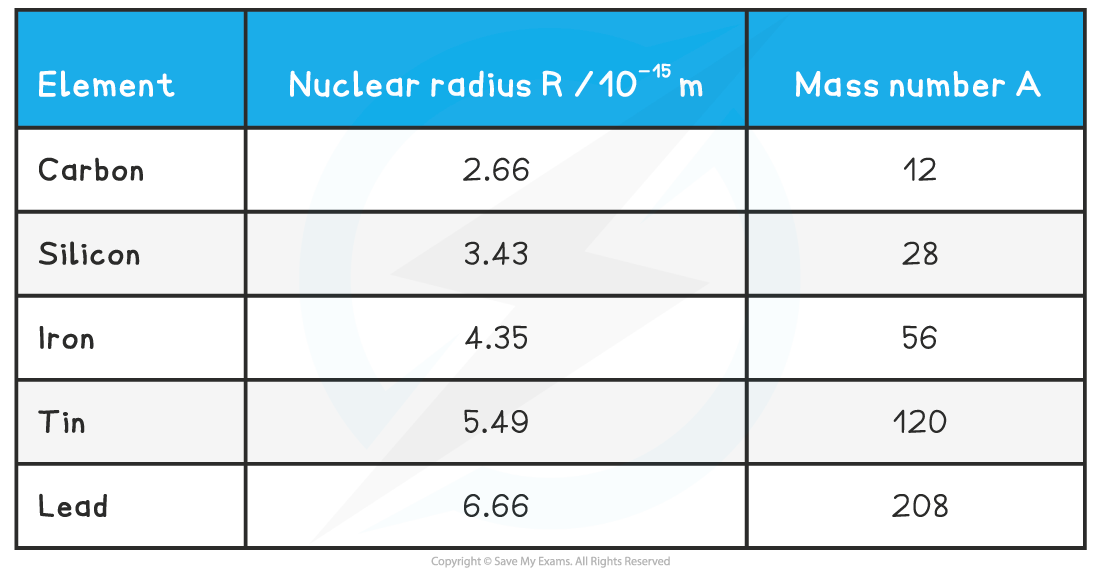
• In general, nuclear radii are of the order 10^–15 m or 1 fm

• The nuclear radius, R, varies with nucleon number, A as follows:

• The key features of this graph are:
  • The graph starts with a steep gradient at the origin
  • Then the gradient gradually decreases to almost horizontal

• This means that
  • As more nucleons are added to a nucleus, the nucleus gets bigger
  • However, the number of nucleons A is not proportional to its size r

• The radius of nuclei depends on the nucleon number, A of the atom
• This makes sense because as more nucleons are added to a nucleus, more space is occupied by the nucleus, hence giving it a larger radius
• The exact relationship between the radius and nucleon number can be determined from experimental data
• By doing this, physicists were able to deduce the following relationship:

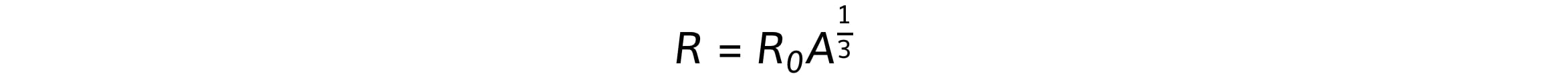
• Where:
  • R = nuclear radius (m)
  • A = nucleon / mass number
  • R₀ = constant of proportionality = 1.05 fm

• Plotting a graph of R against A^{1 / 3} gives a straight line through the origin with the gradient equal to R₀

• It is also possible to plot a logarithmic graph of the relationship which can be derived as follows:

ln R = ln (R₀ A^{1 / 3})

ln R = ln R₀ + ln (A^{1 / 3})

ln R = ln R₀ + 1/3 ln A

• Therefore, a graph of ln R against ln A yields a straight line
• Comparing this to the straight-line equation: y = mx + c
  • y = lnR
  • x = lnA
  • m (the gradient) = 1/3
  • c (y-intercept) = ln R₀

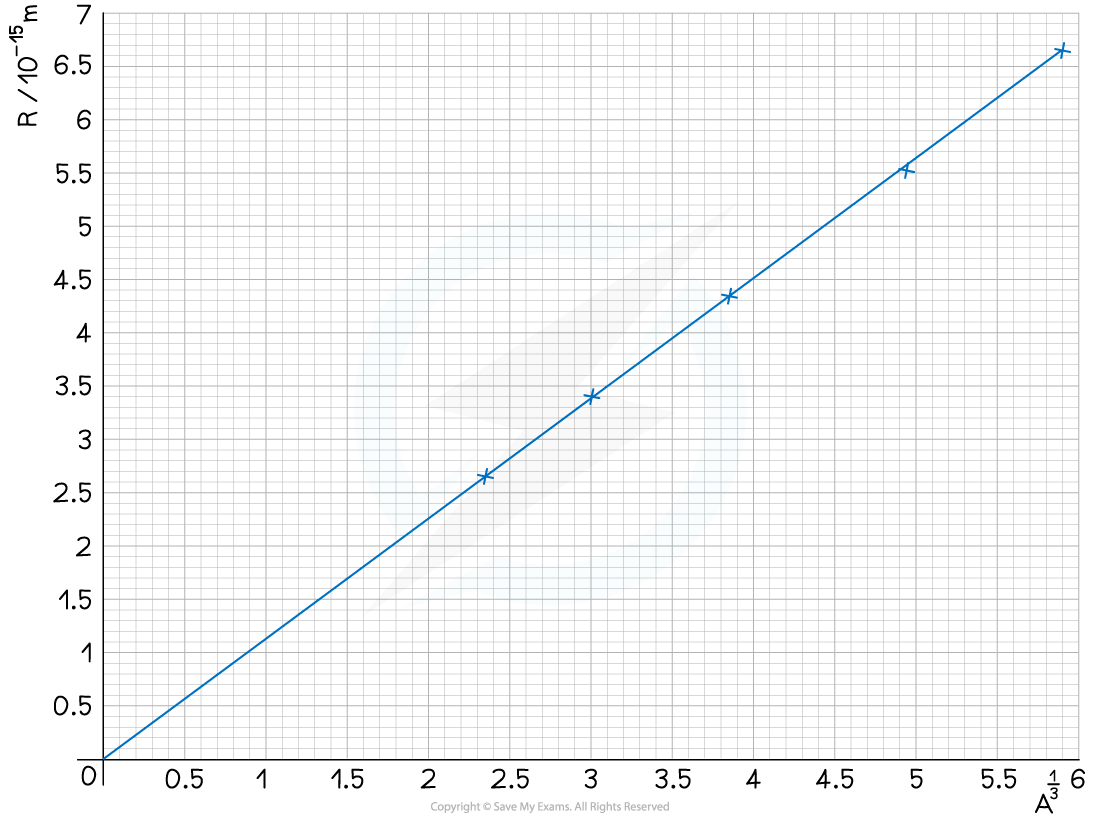
Step 1: Add a column to the table to determine the values for A^{1 / 3}

Step 2: Plot a graph of R against A^{1 / 3} and draw a line of best fit

Step 3: Calculate the gradient

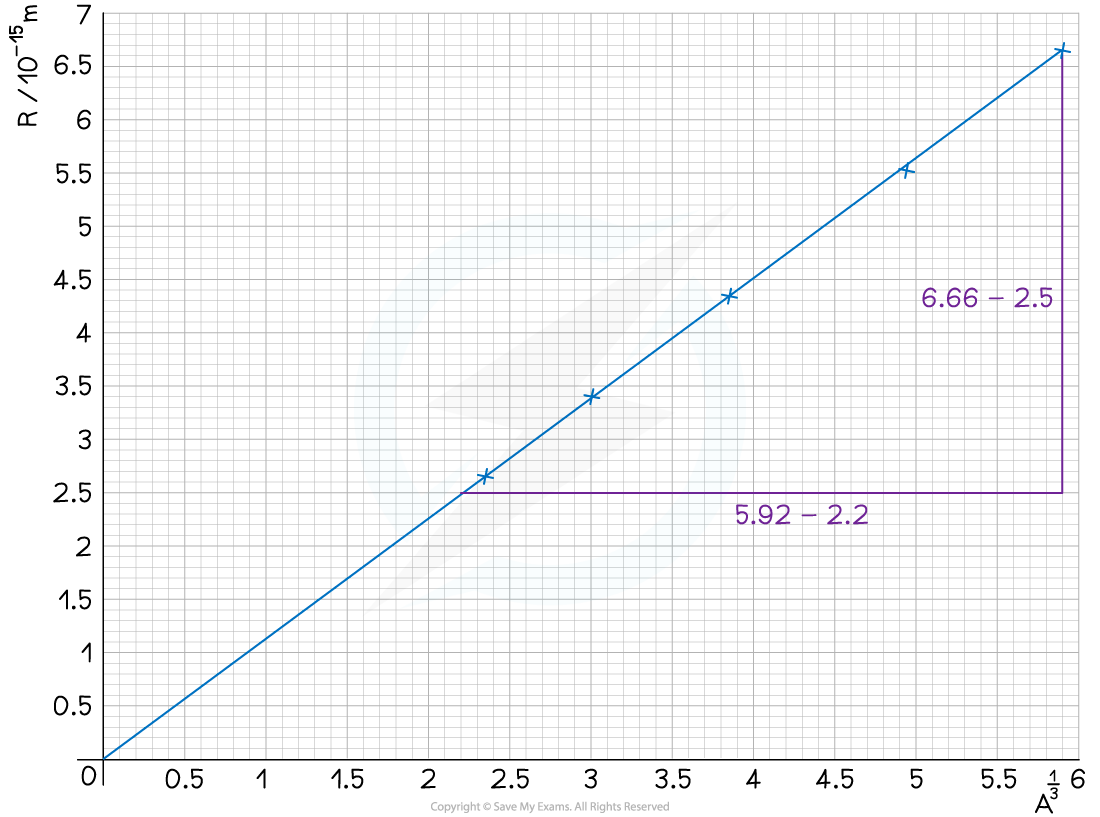
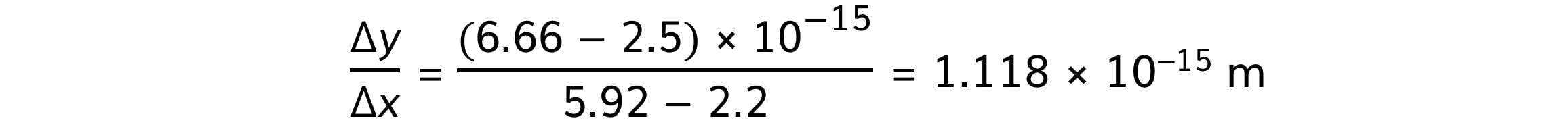
R₀ = 1.12 fm