Nuclear Radius (AQA A Level Physics): Revision Note
Exam code: 7408
Estimating Nuclear Radius
Nuclear radius can be measured experimentally using one of two methods
Rutherford scattering - the closest approach method
Electron scattering
Closest Approach Method
In Rutherford scattering:
Alpha particles are fired at a thin sheet of gold foil
Some of the alpha particles are found to rebound from the gold foil by 180°
Rutherford scattering indicates that there must be an electrostatic repulsion between the alpha particles and the gold nucleus
The alpha particle is fired with an initial kinetic energy
At the point of closest approach
, the repulsive force reduces the speed of the alpha particles to zero momentarily
The initial kinetic energy of the alpha particle is transferred to electric potential energy, which is given by:
Where:
Charge of an alpha particle, Q = 2e
Charge of a gold nucleus, q = 79e
e = elementary charge (C)
r = the radius of closest approach (m)
ε0 = permittivity of free space
At this point, the initial kinetic energy
of the alpha particle is equal to the electric potential energy
of the gold nucleus:
Rearranging for the distance of closest approach
:
This gives a value for the radius of the nucleus, assuming the alpha particle is fired at a high energy

An alpha particle transfers its maximum kinetic energy to maximum potential energy at the distance of closest approach to a gold nucleus
In Rutherford scattering using alpha particles of initial energy 5 MeV:
m
The distance of closest approach is 4.5 × 10−14 m, or 45 fm
For comparison, the actual radius of a gold nucleus is about 6.6 × 10−15 m, or 6.6 fm
Therefore, the closest approach method gives an estimate of the upper limit of the radius of a gold nucleus
Advantages of the Closest Approach Method
Alpha scattering gives a good estimate of the upper limit for a nuclear radius
The mathematics behind this approach are very simple
The alpha particles are scattered only by the protons and not all the nucleons that make up the nucleus
Disadvantages of the Closest Approach Method
Alpha scattering does not give an accurate value for nuclear radius as it will always be an overestimate
This is because it measures the smallest separation between the alpha particle and the gold nucleus, not its radius
Alpha particles contain hadrons which are affected by the strong nuclear force
This affects high-energy alpha particles which get very close to the nucleus (0.5 to 3 fm)
The mathematics in this method cannot account for the effects due to the strong nuclear force
The gold nucleus will recoil as the alpha particle approaches
Alpha particles have a finite size and mass whereas electrons can be treated as a point mass
Very few alpha particles rebound at exactly 180°, so to detect these, a small collision region is required
The alpha particles in the beam are assumed to have the same initial kinetic energy which may not be realistic
The foil target must be extremely thin to prevent multiple scattering
Electron Scattering
Electrons accelerated to close to the speed of light are found to have wave-like properties, such as the ability to diffract
The de Broglie wavelength of an electron is equal to:
Where:
h = Planck's constant
m = mass of an electron (kg)
v = speed of the electrons (m s−1)
This equation shows that as the speed of an electron increases, the smaller its de Broglie wavelength becomes
When a beam of electrons is directed at a thin target, each electron will diffract around a nucleus
This happens because the de Broglie wavelength of a high-speed electron is similar to the size of a nucleus
The resulting diffraction pattern that forms is a central bright spot with dimmer concentric circles around it
From this pattern, a graph of intensity against diffraction angle can be plotted
The size of the nucleus can be determined using the angle of the first minimum intensity
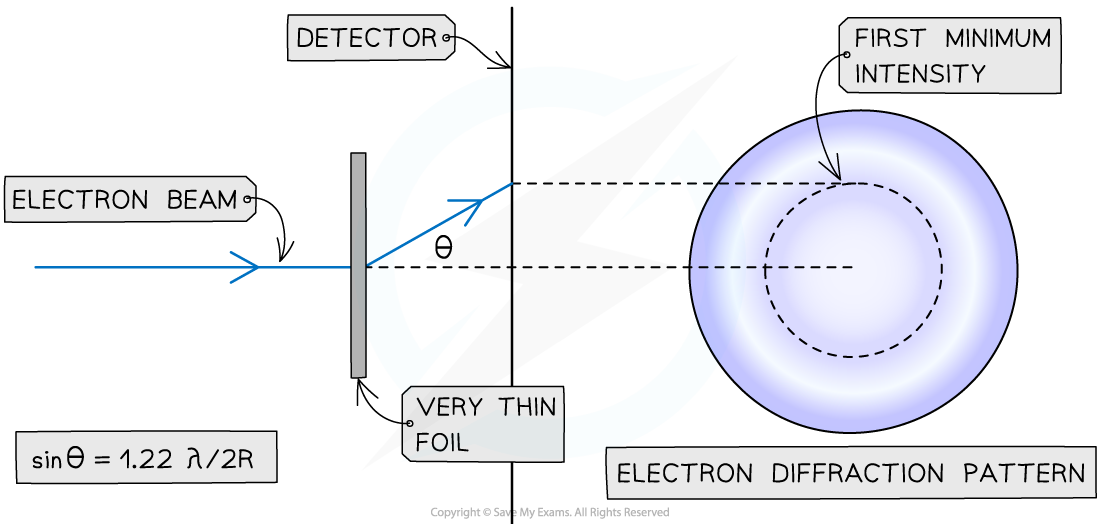
The diffraction pattern produced by passing high-energy electrons through a target foil can be used to determine the nuclear radius
Advantages of Electron Scattering
Electron scattering is much more accurate than the closest approach method
This method gives a direct measurement of the radius of a nucleus
Electrons are leptons, so they are not affected by the strong nuclear force
Disadvantages of Electron Scattering
Electrons must be accelerated to very high speeds to maximise the resolution
This is because significant diffraction takes place when the electron wavelength is similar in size to the nucleus
Higher speeds are needed to shorten the de Broglie wavelength, since
Electrons can be scattered by both protons and neutrons
If there is an excessive amount of scattering, then the first minimum of the electron diffraction can be difficult to determine
Examiner Tips and Tricks
Make sure you're comfortable with the calculations involved in both scattering experiments, as these are common exam questions. You will be expected to remember that the charge of an α-particle is the charge of 2 protons (2 × the charge of an electron)
It is a common misconception that electron diffraction occurs due to the gap between nuclei. This is incorrect as the de Broglie wavelength of an electron is much less than the size of the gap between nuclei, it is much more comparable to the size of the nucleus itself.
An electron diffracts around a nucleus like a sound wave diffracting around a barrier or an obstacle. On the other side of the nucleus (the 'obstacle'), the diffracted waves interfere and produce the concentric ring pattern we observe.
Electron Diffraction by a Nucleus
The graph of intensity against angle obtained through electron diffraction is as follows:

The first minimum of the intensity-angle graph can be used to determine nuclear radius
The pattern formed by this diffraction has a predictable minimum which forms at an angle θ to the original direction according to the equation
To determine an accurate value for nuclear radius R, a multiplication factor of 1.22 is required, as follows:
Where:
θ = angle of the first minimum (degrees)
λ = de Broglie wavelength (m)
d = diameter of the nucleus (m)
R = radius of the nucleus (m)
Worked Example
The graph shows how the relative intensity of the scattered electrons varies with angle due to diffraction by the oxygen-16 nuclei. The angle is measured from the original direction of the beam.
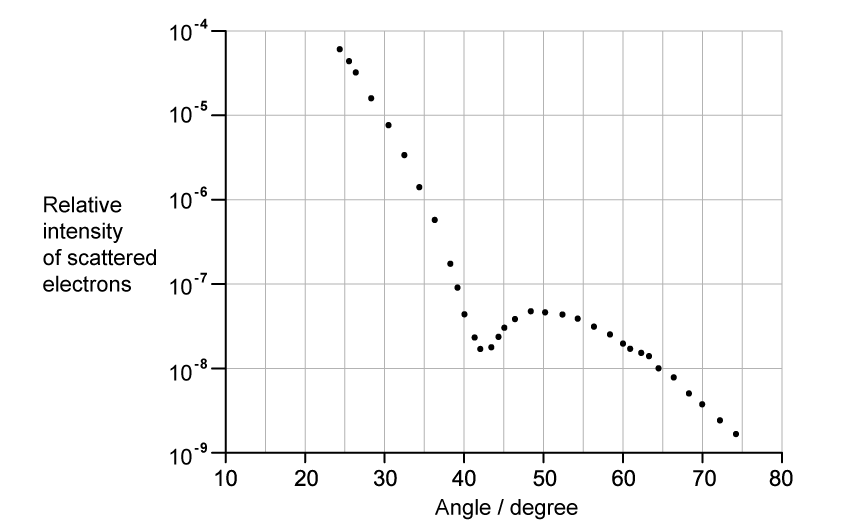
The de Broglie wavelength λ of each electron in the beam is 3.35 × 10−15 m.
Calculate the radius of an oxygen-16 nucleus using information from the graph.
Answer:
Step 1: Identify the first minimum from the graph
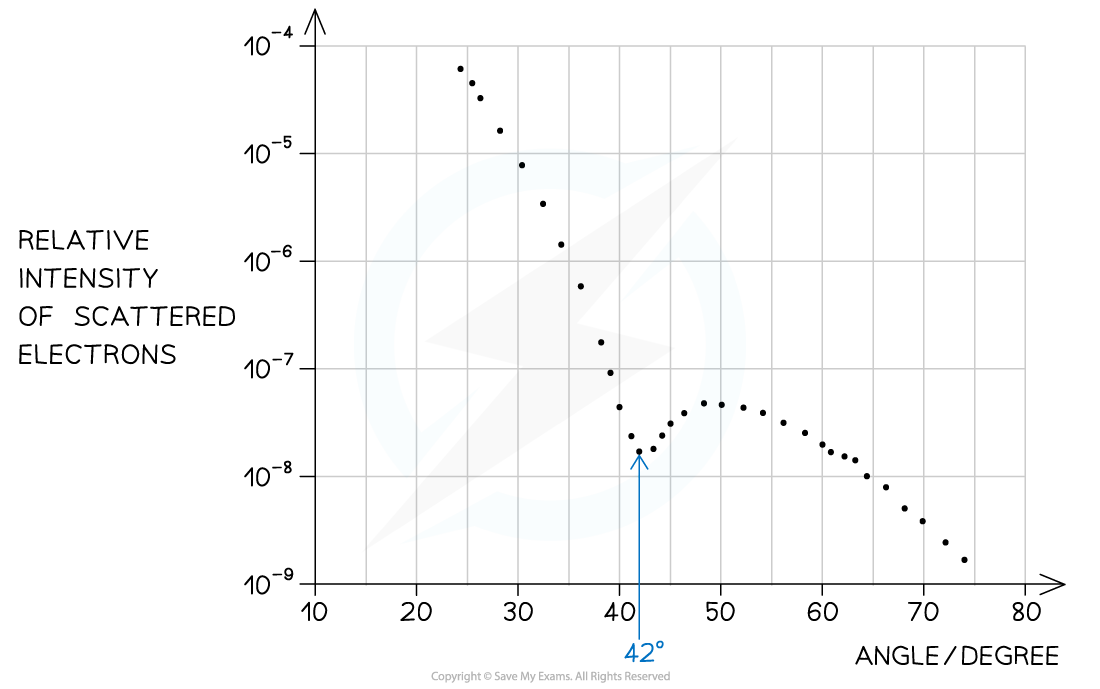
Angle of first minimum, θ = 42°
Step 2: Write out the equation relating the angle, wavelength, and nuclear radius
Step 3: Calculate the nuclear radius, R
= 3.05 × 10−15 m

Unlock more, it's free!
Did this page help you?