Revision NotesExam QuestionsPast Papers
A LevelPhysicsAQARevision NotesNuclear PhysicsRadioactive DecayApplications of Radioactivity

Applications of Radioactivity (AQA A Level Physics)

Revision Note

Katie M

Author

Katie M

Last updated

Applications of Radioactivity

  • Radioactivity has a wide variety of uses in industry, agriculture and medicine

  • Some of the main uses are

    • Nuclear power

    • In medicine e.g. radiotherapy, tracers and sterilising equipment

    • Radiocarbon dating of archaeological artefacts

    • Uranium-lead dating of rock samples

    • Radioisotope power systems

Radiocarbon Dating

  • The isotope carbon-14 is commonly used in radioactive dating

  • It forms as a result of cosmic rays knocking out neutrons from nuclei, which then collide with nitrogen nuclei in the air:

n presubscript blank presuperscript 1 space plus space N presubscript blank presuperscript 14 space rightwards arrow space C presubscript blank presuperscript 14 space plus thin space p presubscript blank presuperscript 1

  • All living organisms absorb carbon-14, but after they die they do not absorb any more

  • The proportion of carbon-14 is constant in living organisms as carbon is constantly being replaced during the period they are alive

  • When they die, the activity of carbon-14 in the organic matter starts to fall, with a half-life of around 5730 years

  • Samples of living material can be tested by comparing the current amount of carbon-14 in them and compared to the initial amount (which is based on the current ratio of carbon-14 to carbon-12), and hence they can be dated

Reliability of Carbon Dating

  • Carbon dating is a highly reliable method for estimating the ages of samples between 500 and 60 000 years old

  • This range can be explained by looking at the decay curve of carbon-14:

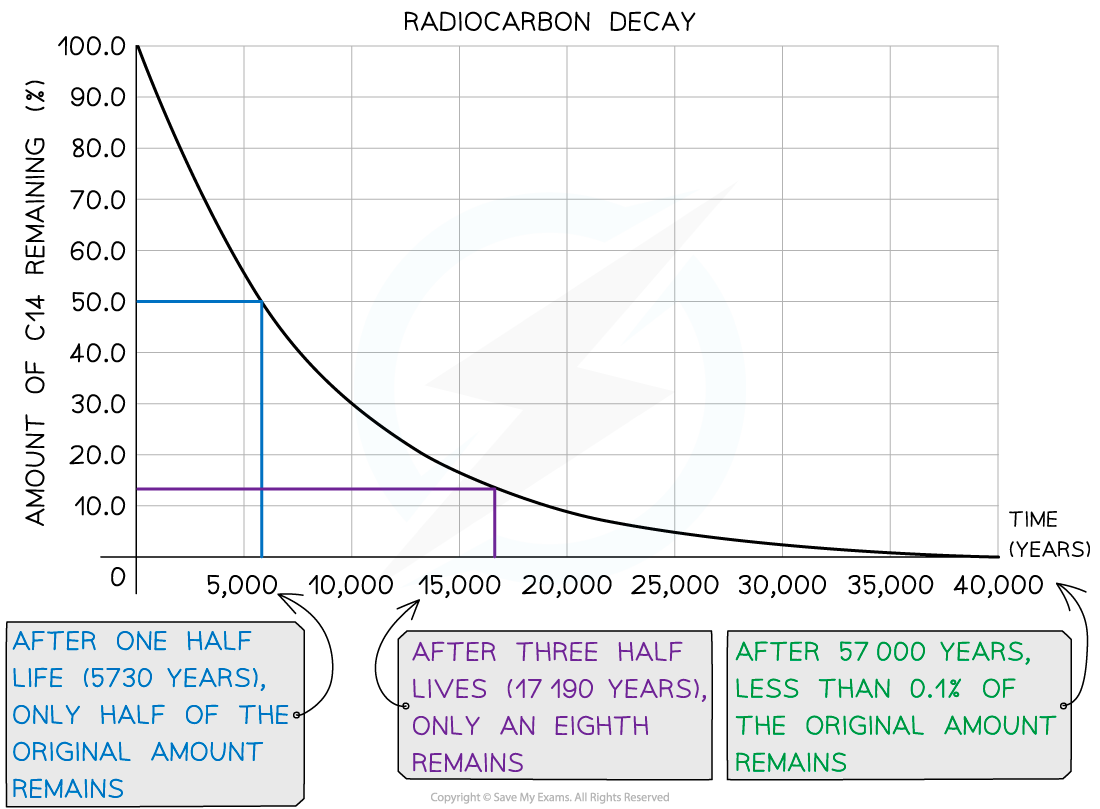
Radiocarbon Decay, downloadable AS & A Level Physics revision notes

Carbon-14 decay curve used for radiocarbon dating

  • If the sample is less than 500 years old:

    • The activity of the sample will be too high to measure small changes accurately

    • Therefore, the ratio of carbon-14 to carbon-12 will be too high to determine an accurate age

  • If the sample is more than 60 000 years old:

    • The activity will be too low to distinguish between changes in the sample and background radiation

    • Therefore, the ratio of carbon-14 to carbon-12 will be too small to determine an accurate age

Uranium-Lead Dating

  • For many years, scientists could not agree on the age of the Earth

  • Until recently, the Earth was believed to be only millions of years old

  • Over the last century, radiometric dating methods have enabled scientists to discover the age of the Earth is many billions of years old

  • The most critical of these methods is uranium-lead dating

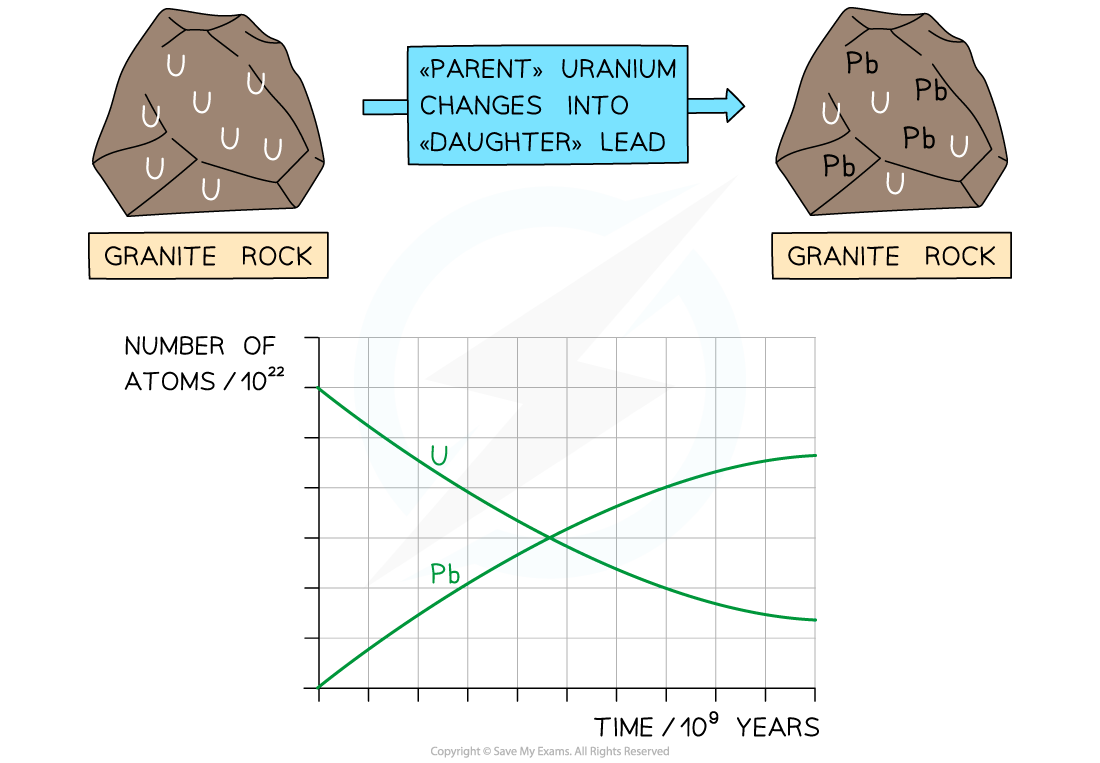
Uranium atoms decay whilst the number of lead atoms increases

  • Initially, there is only uranium in the rock, but over time, the uranium decays via a decay chain which ends with lead-206, which is a stable isotope

  • Uranium-238 has a half-life of 4.5 billion years

  • Over time, the ratio of lead-206 atoms to uranium-238 atoms increases

  • The ratio of uranium to lead in a sample of rock can then be used to determine its age

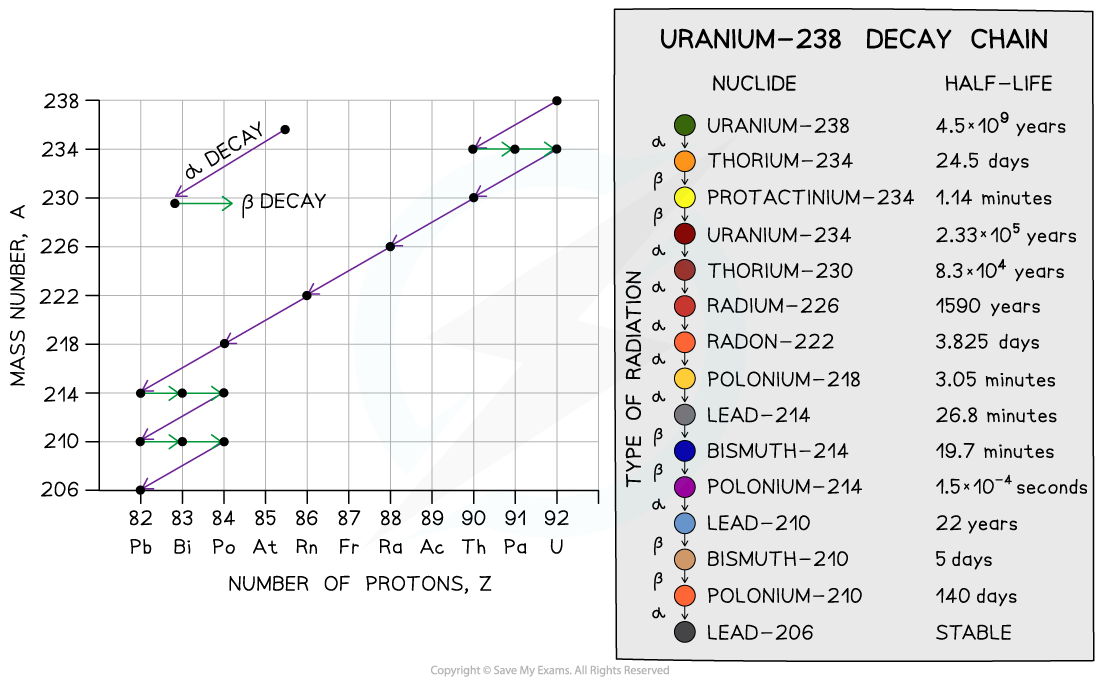
Uranium Decay Chain, downloadable AS & A Level Physics revision notes

Uranium-238 decay chain

Radioisotope Power Systems

  • The decay of an isotope may release energy as heat

  • Radioisotopic power systems are designed to transform this heat into electrical power

  • Such devices have been used to power space probes and satellites

  • Typically, plutonium-238 is used as fuel, with 1 g generating a power output of about 500 mW

Worked Example

A space probe uses a source containing 4.0 kg of plutonium-238.

Plutonium-238 is an alpha-emitter with a half-life of 87.7 years. Each alpha decay releases 5.5 MeV per emission. The space probe converts this into electrical energy with an efficiency of 32%.

The space probe can continue to operate as long as the power output is maintained at 0.4 kW or above.

Estimate the time, in years, the source is expected to supply power to the space probe.

Answer:

Step 1: List the known quantities

  • Mass of Pu-238 = 4.0 kg = 4000 g

  • Molar mass of Pu-238 = 238 g mol−1

  • Avogadro's constant, N subscript A = 6.02 × 1023 mol−1

  • Half-life of Pu-238 = 87.7 years

  • Energy released per alpha decay = 5.5 MeV

  • 1 electronvolt (eV) = 1.6 × 10−19 J

  • Efficiency = 32% = 0.32

  • Final power output, P = 0.4 kW = 400 W

Step 2: Calculate the initial number of nuclei present in the source

  • 238 g of plutonium-238 contains 6.02 × 1023 atoms (Avogadro's number), so in 4 kg:

Number of nuclei: N space equals space fraction numerator m a s s space cross times space N subscript A over denominator m o l a r space m a s s end fraction

Initial number of nuclei: N subscript 0 space equals space fraction numerator 4000 space cross times space open parentheses 6.02 cross times 10 to the power of 23 close parentheses over denominator 238 end fraction space equals space 1.012 cross times 10 to the power of 25 nuclei

Step 3: Calculate the initial activity of the source

Decay constant:  lambda space equals space fraction numerator ln space 2 over denominator t subscript 1 divided by 2 end subscript end fraction

Activity: A space equals space lambda N

  • Combining these gives:

Initial activity: A subscript 0 space equals space fraction numerator N subscript 0 space ln space 2 over denominator t subscript 1 divided by 2 end subscript end fraction

A subscript 0 space equals space fraction numerator open parentheses 1.012 cross times 10 to the power of 25 close parentheses space cross times space ln space 2 over denominator 87.7 space cross times space open parentheses 24 cross times 60 cross times 60 cross times 365 close parentheses end fraction space equals space 2.5357 cross times 10 to the power of 15Bq

Step 4: Calculate the initial power output of the source

Power output: P space equals space fraction numerator increment E over denominator increment t end fraction

Energy released per decay: E space equals space open parentheses 5.5 cross times 10 to the power of 6 close parentheses space cross times space open parentheses 1.6 cross times 10 to the power of negative 19 end exponent close parentheses

  • Activity represents the decays per second, so:

Initial power output: P subscript 0 space equals space A subscript 0 E

P subscript 0 space equals space open parentheses 2.5357 cross times 10 to the power of 15 close parentheses space cross times space open parentheses 5.5 cross times 10 to the power of 6 close parentheses space cross times space open parentheses 1.6 cross times 10 to the power of negative 19 end exponent close parentheses space equals space 2231 W

  • The electrical power transferred to the probe is:

P subscript 0 space equals space 2231 space cross times space 0.32 space equals space 714 W

Step 5: Use the exponential decay equation to calculate the time of operation

  • The power available is proportional to the activity of the isotope, so: 

Exponential decay of power: P space equals space P subscript 0 space e to the power of negative lambda t end exponent

fraction numerator P over denominator P subscript 0 space end fraction space equals space e to the power of negative lambda t end exponent

ln open parentheses fraction numerator P over denominator P subscript 0 space end fraction close parentheses space equals space minus lambda t

t space equals space minus 1 over lambda space ln open parentheses P over P subscript 0 close parentheses space equals space minus fraction numerator t subscript 1 divided by 2 end subscript over denominator ln space 2 end fraction space ln open parentheses P over P subscript 0 close parentheses

t space equals space minus fraction numerator 87.7 over denominator ln space 2 end fraction space ln open parentheses 400 over 714 close parentheses space equals space 73.3 years

  • Therefore, the source is expected to supply power to the space probe for 73.3 years

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Half-LifeNext:Nuclear Instability
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.