A LevelPhysicsAQARevision NotesNuclear PhysicsRadioactive DecayHalf-Life

Half-Life (AQA A Level Physics) : Revision Note

Katie M

Author

Katie M

Last updated

Half-Life

  • Half-life is defined as:

The average time taken for a given number of nuclei of a particular isotope to halve

  • Since activity A is proportional to the number of undecayed nuclei N, the activity of the sample will also halve

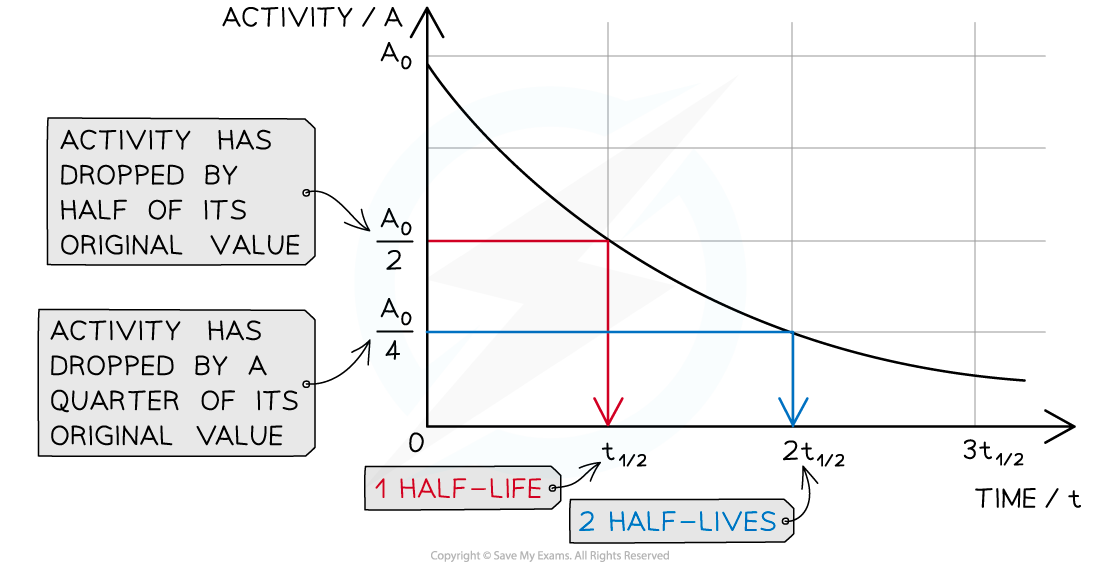
Half-life Graph, downloadable IGCSE & GCSE Physics revision notes

When a time equal to the half-life passes, the activity falls by half, when two half-lives pass, the activity falls by another half (which is a quarter of the initial value)

  • To find an expression for half-life, start with the equation for exponential decay:

N space equals space N subscript 0 space e to the power of negative lambda t end exponent

  • Where:

    • N = number of nuclei remaining in a sample

    • N0 = the initial number of undecayed nuclei (when t = 0)

    • λ = decay constant (s-1)

    • t = time interval (s)

  • When time t is equal to the half-life t subscript 1 divided by 2 end subscript, the activity N of the sample will be half of its original value, so N space equals space 1 half N subscript 0

1 half N subscript 0 space equals space N subscript 0 space e to the power of negative lambda t subscript 1 divided by 2 end subscript end exponent

  • The formula can then be derived by first, dividing both sides by N subscript 0:

1 half space equals space e to the power of negative lambda t subscript 1 divided by 2 end subscript end exponent

  • Then, taking the natural log of both sides:

ln space open parentheses 1 half close parentheses space equals space minus lambda t subscript 1 divided by 2 end subscript

  • Finally, applying properties of logarithms:

lambda t subscript 1 divided by 2 end subscript space equals space ln space 2

  • Therefore, half-life t subscript 1 divided by 2 end subscript can be calculated using the equation:

t subscript 1 divided by 2 end subscript space equals space fraction numerator ln space 2 over denominator lambda end fraction space asymptotically equal to space fraction numerator 0.693 over denominator lambda end fraction

  • This equation shows that half-life t subscript 1 divided by 2 end subscript and the radioactive decay rate constant λ are inversely proportional

    • Therefore, the shorter the half-life, the larger the decay constant and the faster the decay

Worked Example

Strontium-90 is a radioactive isotope with a half-life of 28.0 years. A sample of Strontium-90 has an activity of 6.4 × 109 Bq.

Calculate the decay constant lambda, in s–1, of Strontium-90.

Answer:

Step 1: Convert the half-life into seconds

  • t subscript 1 divided by 2 end subscript = 28 years = 28 × (365 × 24 × 60 × 60) = 8.83 × 108 s

Step 2: Write the equation for half-life

t subscript 1 divided by 2 end subscript space equals space fraction numerator ln space 2 over denominator lambda end fraction

Step 3: Rearrange for λ and calculate

t subscript 1 divided by 2 end subscript space equals space fraction numerator ln space 2 over denominator 8.83 cross times 10 to the power of 8 end fraction space equals space 7.85 cross times 10 to the power of negative 10 end exponent space straight s to the power of negative 1 end exponent

Examiner Tips and Tricks

Although you may not be expected to derive the half-life equation, make sure you're comfortable with how to use it in calculations such as that in the worked example.

Half-Life from Decay Curves

  • The half-life of a radioactive substance can be determined from decay curves and log graphs

  • Since half-life is the time taken for the initial number of nuclei (or activity) to reduce by half, it can be found by

    • drawing a line to the curve at the point where the activity has dropped to half of its original value

    • drawing a line from the curve to the time axis, this is the half-life

Log Graphs

  • Straight-line graphs tend to be more useful than curves for interpreting data

    • Nuclei decay exponentially, therefore, to achieve a straight line plot, logarithms can be used

  • Take the exponential decay equation for the number of nuclei

N space equals space N subscript 0 space e to the power of negative lambda t end exponent

  • Taking the natural logs of both sides

ln space N space equals space ln space open parentheses N subscript 0 close parentheses space minus space lambda t

  • In this form, this equation can be compared to the equation of a straight line

y space equals space m x space plus thin space c

  • Where:

    • y-axis variable, y space equals space ln space N

    • x-axis variable, x space equals space t

    • gradient, m space equals space minus lambda

    • y-intercept, c space equals space ln space open parentheses N subscript 0 close parentheses

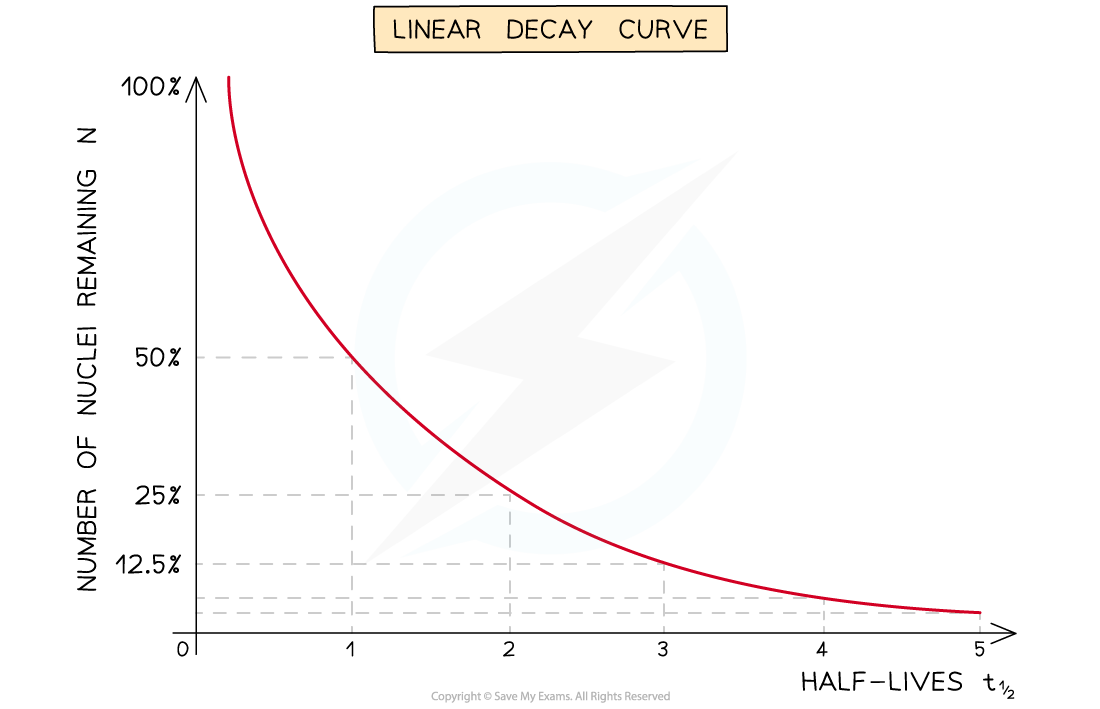
  • Half-lives can be found in a similar way to the decay curve but the intervals will be regular as shown below:

Half Life Decay Curves 1, downloadable AS & A Level Physics revision notes
Half Life Decay Curves 2, downloadable AS & A Level Physics revision notes

Worked Example

The radioisotope technetium is used extensively in medicine. The graph below shows how the activity of a sample varies with time.

Worked Example - Half Life Curve, downloadable AS & A Level Physics revision notes

Determine:

a) The decay constant for technetium

b) The number of technetium atoms remaining in the sample after 24 hours

Answer:

Part (a)

Step 1: Draw lines on the graph to determine the time it takes for technetium to drop to half of its original activity

Worked Example - Half Life Curve Ans a, downloadable AS & A Level Physics revision notes

Step 2: Read the half-life from the graph and convert to seconds

  • t subscript 1 divided by 2 end subscript = 6 hours = 6 × 60 × 60 = 21 600 s

Step 3: Write out the half life equation

t subscript 1 divided by 2 end subscript space equals space fraction numerator ln space 2 over denominator lambda end fraction

Step 4: Calculate the decay constant

t subscript 1 divided by 2 end subscript space equals space fraction numerator ln space 2 over denominator 21 space 600 end fraction space equals space 3.2 cross times 10 to the power of negative 5 end exponent space straight s to the power of negative 1 end exponent

Part (b)

Step 1: Draw lines on the graph to determine the activity after 24 hours

Worked Example - Half Life Curve Ans b, downloadable AS & A Level Physics revision notes

  • At t = 24 hours, A = 0.5 × 107 Bq

Step 2: Write out the activity equation

A space equals space lambda N

Step 3: Calculate the number of atoms remaining in the sample

N space equals space A over lambda space equals space fraction numerator 0.5 cross times 10 to the power of 7 over denominator 3.2 cross times 10 to the power of negative 5 end exponent end fraction space equals space 1.56 cross times 10 to the power of 11

You've read 1 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

  • I would just like to say a massive thank you for putting together such a brilliant, easy to use website.I really think using this site helped me secure my top gradesin science and maths. You really did save my exams! Thank you.

    Beth
    IGCSE Student

  • This website is soooo useful and I can’t ever thank you enough for organising questions by topic like this. Furthermore, the name of the website could not have been more appropriate as it literally did SAVE MY EXAMS!

    Fathima
    A Level Student
Test yourself

Did this page help you?

Previous:Exponential DecayNext:Applications of Radioactivity
Katie M

Author: Katie M

Expertise: Physics Content Creator

Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

Download notes on Half-Life