Circular Path of Particles (AQA A Level Physics)

Motion of a Charged Particle in a Magnetic Field

• When a charged particle enters a uniform magnetic field, it travels in a circular path

• This is because the direction of the magnetic force F will always be

  • perpendicular to the particle's velocity v

  • directed towards the centre of the path, resulting in circular motion

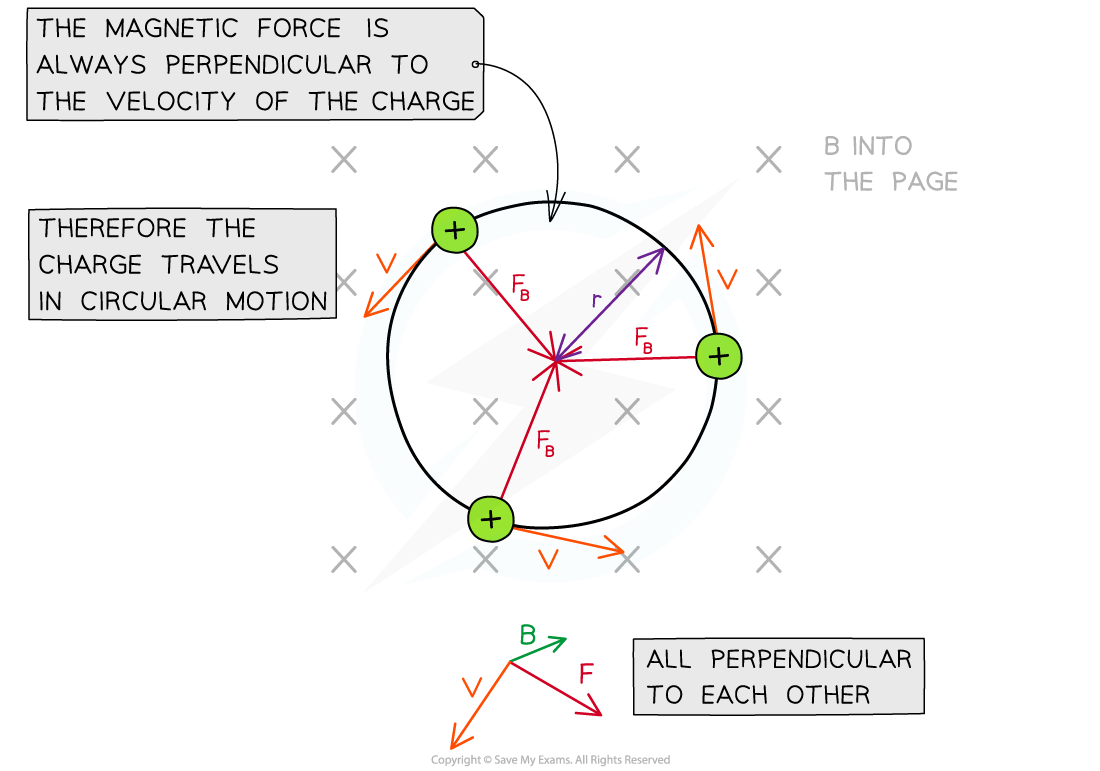
In a magnetic field, a charged particle travels in a circular path as the force, velocity and field are all perpendicular

• The magnetic force F provides the centripetal force on the particle

• The equation for centripetal force is:

• Equating this to the magnetic force on a moving charged particle gives the expression:

• Rearranging for the radius r gives an expression for the radius of the path of a charged particle in a perpendicular magnetic field:

• Where:

  • r = radius of the path (m)

  • m = mass of the particle (kg)

  • v = linear velocity of the particle (m s⁻¹)

  • B = magnetic field strength (T)

  • Q = charge of the particle (C)

• This equation shows that:

  • Faster moving particles with speed v move in larger circles (larger r): 

  • Particles with greater mass m move in larger circles: 

  • Particles with greater charge q move in smaller circles:  

  • Particles moving in a strong magnetic field B move in smaller circles: 

• The centripetal acceleration is in the same direction as the magnetic (centripetal) force

• This can be found using Newton's second law:

Cyclotrons

• A cyclotron is a type of particle accelerator which

  • makes use of the circular trajectory of charged particles in a magnetic field to create a spiral path

  • accelerates charged particles, such as protons, to very high speeds

• Cyclotrons have many medical applications, such as:

  • to produce tracers for imaging

  • to create high-energy beams of radiation for radiotherapy

• Cyclotrons consist of:

  • two hollow semicircular electrodes called 'dees'

  • a strong uniform magnetic field 

  • an alternating electric field

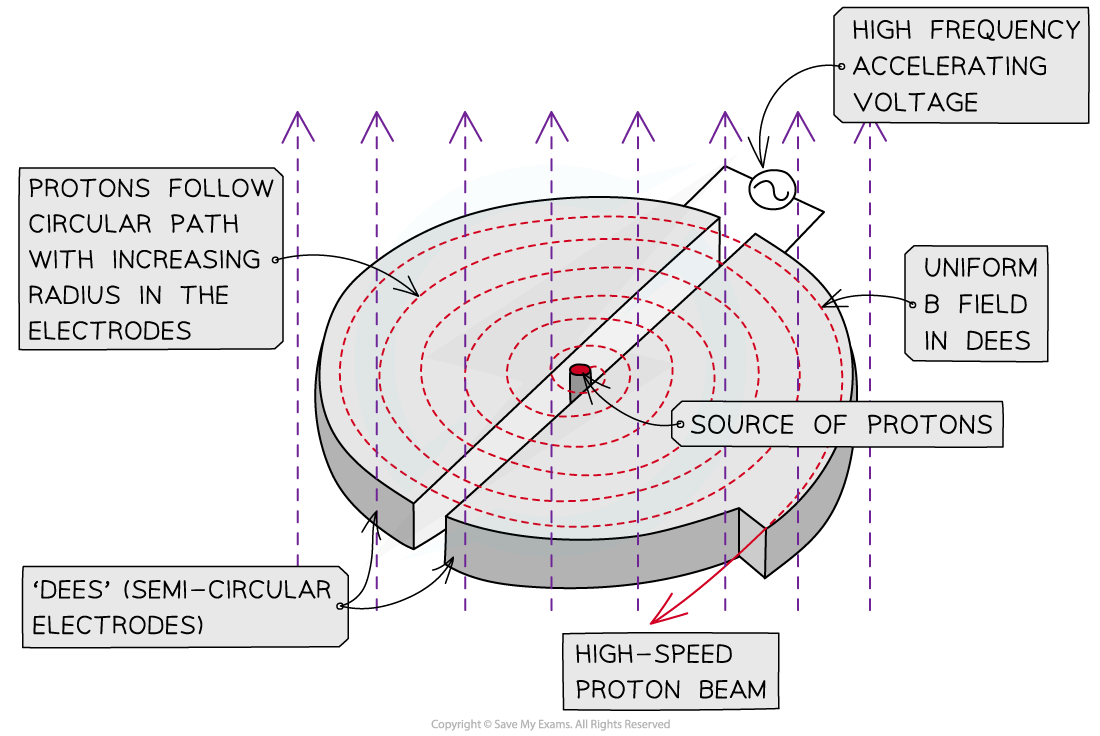
A cyclotron is a type of particle accelerator that utilises electric and magnetic fields to create high-energy beams of charged particles, such as protons

Function of a Cyclotron

1.  Entering the dees

• There is a source of charged particles at the centre of the cyclotron

• A magnetic field is applied perpendicular to the path of the particles 

• A magnetic force acts in a direction perpendicular to the field and the path of the particles

• This causes the particles to move in a circular path when inside the dees

2.  Crossing the gap between dees

• There is a gap between each semi-circular dee

• An electric field is applied in the gaps between the dees

• An electric force acts on the charged particles causing them to accelerate

• This causes them to enter the next dee at a higher speed and follow a path with a larger radius

3.  Leaving the dees

• The charged particles travel with constant speed in the dees

• This means the time spent in one dee is constant 

• The direction of the electric field alternates each time the particles reach a gap 

• This means they will always accelerate towards the opposite dee

• This process repeats as the particles spiral outwards until they leave the cyclotron at the desired speed

Role of the magnetic field in a cyclotron

• In a cyclotron, the role of the uniform magnetic field is

  To supply the centripetal force needed to keep the particles moving in circular motion

• As the charged particles travel around a single dee they

  • follow a circular path of constant radius

  • move at a constant speed 

Role of the electric field in a cyclotron

• In a cyclotron, the role of the alternating electric field is

  To accelerate the particles between the dees

• As the charged particles travel across the gap between dees they

  • gain additional energy = QV

  • move faster and follow a path with a larger radius as they enter the next dee