Force on a Moving Charge (AQA A Level Physics): Revision Note
Exam code: 7408
Magnetic Force on a Moving Charge
A moving charge produces its own magnetic field
When interacting with an applied magnetic field, it will experience a force
The force F on an isolated particle with charge Q moving with speed v at an angle θ to a magnetic field with flux density B is defined by the equation
Where:
F = magnetic force on the particle (N)
B = magnetic flux density (T)
Q = charge of the particle (C)
v = speed of the particle (m s−1)
Current is taken as the rate of flow of positive charge (i.e. conventional current)
This means that the direction of the current for a flow of negative charge (e.g. a beam of electrons) is in the opposite direction to its motion
As with a current-carrying conductor, the maximum force on a charged particle occurs when it travels perpendicular to the field
This is when θ = 90°, so sin θ = 1
The equation for the magnetic force becomes:
F, B and v are mutually perpendicular, therefore:
If the direction of the particle's motion changes, the magnitude of the force will also change
If the particle travels parallel to a magnetic field, it will experience no magnetic force
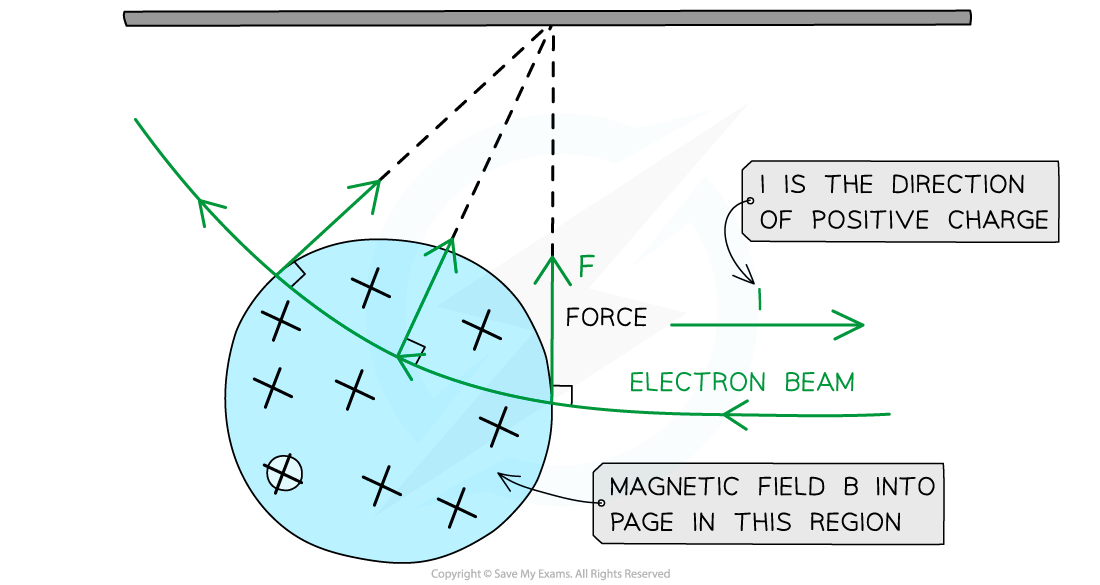
The force on an isolated moving charge is perpendicular to its motion and the magnetic field B
From the diagram above, when a beam of electrons enters a magnetic field which is directed into the page:
Electrons are negatively charged, so current I is directed to the right (as motion v is directed to the left)
Using Fleming’s left hand rule, the force on an electron will be directed upwards
Worked Example
An electron moves in a uniform magnetic field of flux density 0.2 T at a velocity of 5.3 × 107 m s−1.
Calculate the force on the electron when it moves perpendicular to the field.
Answer:
Step 1: Write out the known quantities
Velocity of the electron, v = 5.3 × 107 m s−1
Charge of an electron, Q = 1.60 × 10−19 C
Magnetic flux density, B = 0.2 T
Step 2: Write down the equation for the magnetic force on an isolated particle
The electron moves perpendicular (θ = 90°) to the field, so sin θ = 1
Step 3: Substitute in values, and calculate the force on the electron
F = (0.2) × (1.60 × 10−19) × (5.3 × 107) = 1.7 × 10−12 N (2 s.f.)
Examiner Tips and Tricks
Remember not to mix this up with F = BIL!
F = BIL is for a current-carrying conductor
F = BQv is for an isolated moving charge (which may be inside a conductor)
Direction of Force on a Moving Charge
The direction of the magnetic force on a charged particle depends on
The direction of flow of current
The direction of the magnetic field
This can be found using Fleming's left-hand rule
The second finger represents the current flow or the flow of positive charge
For a positive charge, the current points in the same direction as its velocity
For a negative charge, the current points in the opposite direction to its velocity
Fleming’s left-hand rule allows us to determine the direction of the force on a charged particle
When a positive charge enters a magnetic field from left to right, using Fleming's left-hand rule:
The first finger (field) points into the page
The second finger (current) points to the right
The thumb (force) points upwards
When a charged particle moves in a uniform magnetic field, the force acts perpendicular to the field and the particle's velocity
As a result, it follows a circular path
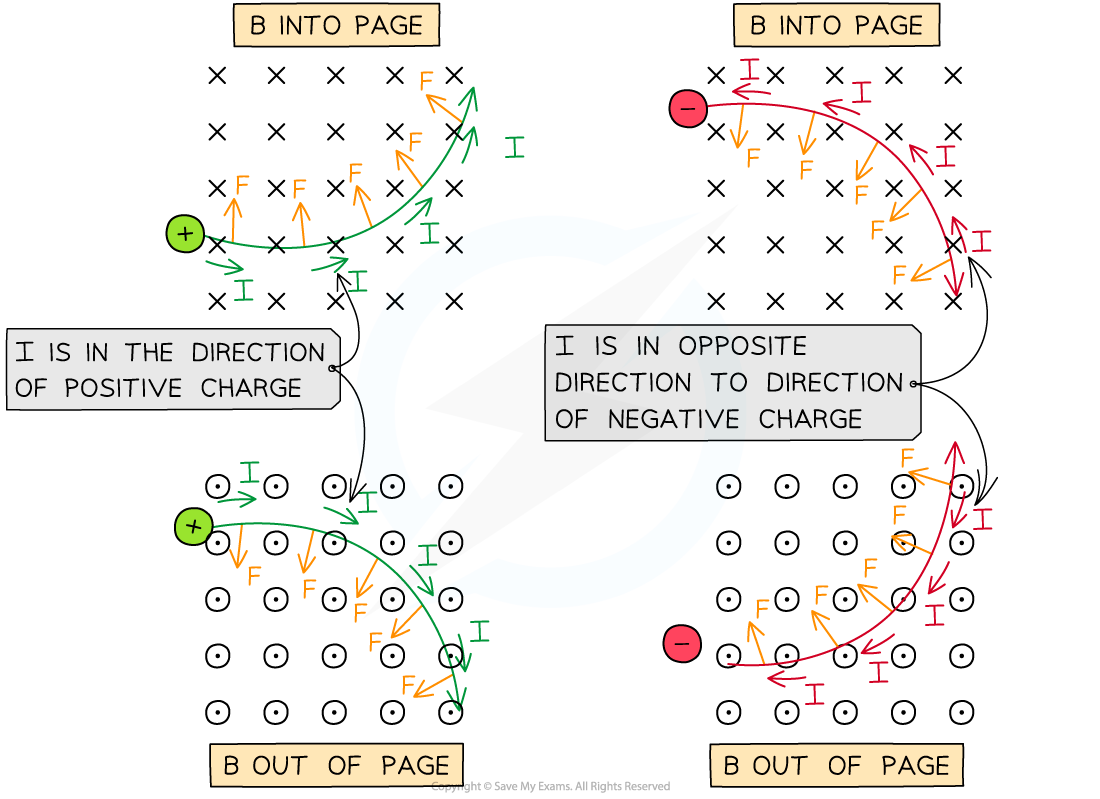
The direction of the magnetic force F on positive and negative particles in a B field in and out of the page
Examiner Tips and Tricks
Remember not to get this mixed up with Fleming's right-hand rule. That is used for a generator (or dynamo), where a current is induced in the conductor. Fleming's left-hand rule is sometimes referred to as the 'Fleming's left-hand rule for motors'.
Unlock more, it's free!
Join the 100,000+ Students that ❤️ Save My Exams
the (exam) results speak for themselves:
Was this revision note helpful?
Build on this topic
