Charge & Discharge Graphs (AQA A Level Physics): Revision Note
Exam code: 7408
Capacitor Charge & Discharge Graphs
Charging
Capacitors are charged by a power supply (eg. a battery)
When charging, the electrons are pulled from the plate connected to the positive terminal of the power supply
Hence the plate nearest the positive terminal is positively charged
They travel around the circuit and are pushed onto the plate connected to the negative terminal
Hence the plate nearest the negative terminal is negatively charged
As the negative charge builds up, fewer electrons are pushed onto the plate due to electrostatic repulsion from the electrons already on the plate
When no more electrons can be pushed onto the negative plate, the charging stops
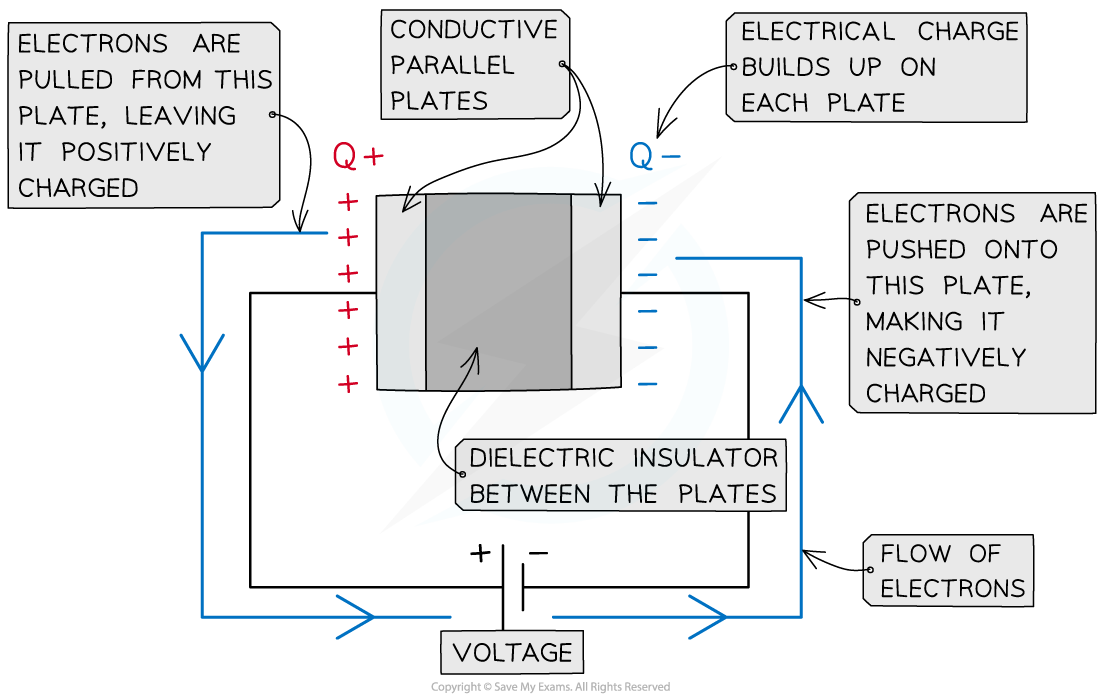
A parallel plate capacitor is made up of two conductive plates with opposite charges building up on each plate
At the start of charging, the current is large and gradually falls to zero as the electrons stop flowing through the circuit
The current decreases exponentially
This means the rate at which the current decreases is proportional to the amount of current it has left
Since an equal but opposite charge builds up on each plate, the potential difference between the plates slowly increases until it is the same as that of the power supply
Similarly, the charge of the plates slowly increases until it is at its maximum charge defined by the capacitance of the capacitor

Graphs of variation of current, p.d and charge with time for a capacitor charging through a battery
The key features of the charging graphs are:
The shapes of the p.d. and charge against time graphs are identical
The current against time graph is an exponential decay curve
The initial value of the current starts on the y axis and decreases exponentially
The initial value of the p.d and charge starts at 0 up to a maximum value
Discharging
Capacitors are discharged through a resistor with no power supply present
The electrons now flow back from the negative plate to the positive plate until there are equal numbers on each plate and no potential difference between them
Charging and discharging is commonly achieved by moving a switch that connects the capacitor between a power supply and a resistor
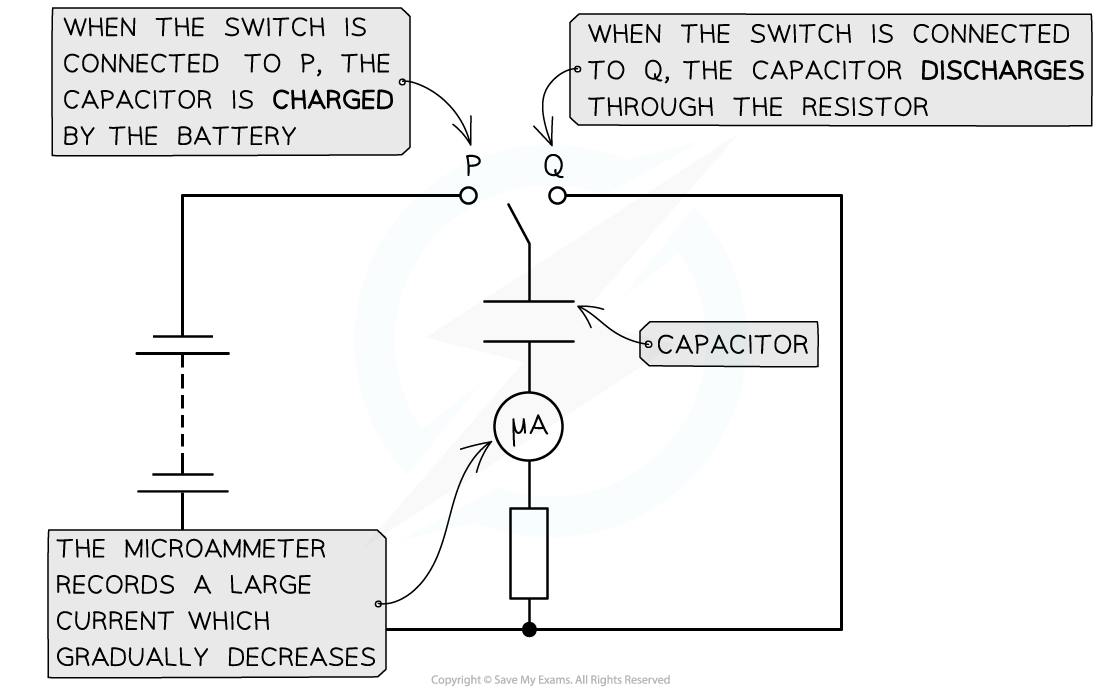
The capacitor charges when connected to terminal P and discharges when connected to terminal Q
At the start of discharge, the current is large (but in the opposite direction to when it was charging) and gradually falls to zero
As a capacitor discharges, the current, p.d and charge all decrease exponentially
This means the rate at which the current, p.d or charge decreases is proportional to the amount of current, p.d or charge it has left
The graphs of the variation with time of current, p.d and charge are all identical and follow a pattern of exponential decay

Graphs of variation of current, p.d and charge with time for a capacitor discharging through a resistor
The key features of the discharge graphs are:
The shape of the current, p.d. and charge against time graphs are identical
Each graph shows exponential decay curves with decreasing gradient
The initial values (typically called I0, V0 and Q0 respectively) start on the y axis and decrease exponentially
The rate at which a capacitor discharges depends on the resistance of the circuit
If the resistance is high, the current will decrease and charge will flow from the capacitor plates more slowly, meaning the capacitor will take longer to discharge
If the resistance is low, the current will increase and charge will flow from the capacitor plates quickly, meaning the capacitor will discharge faster
Examiner Tips and Tricks
Make sure you're comfortable with sketching and interpreting charging and discharging graphs, as these are common exam questionsRemember that conventional current flow is in the opposite direction to the electron flow
Properties of Capacitor Discharge Graphs
From electricity, the charge is defined:
ΔQ = IΔt
Where:
I = current (A)
ΔQ = change in charge (C)
Δt = change in time (s)
This means that the area under a current-time graph for a charging (or discharging) capacitor is the charge stored for a certain time interval
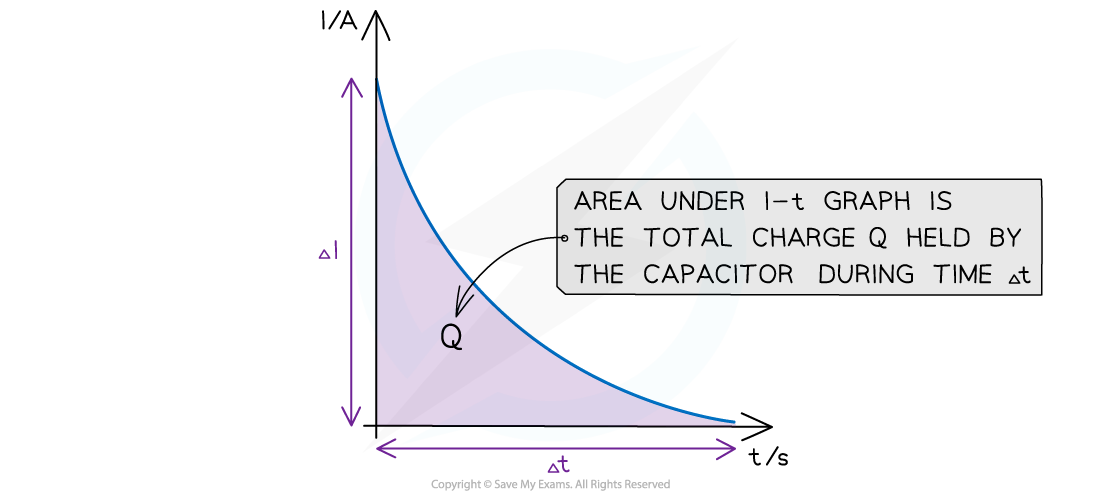
The area under the I-t graph is the total charge stored in the capacitor in the time interval Δt
Rearranging for the current:
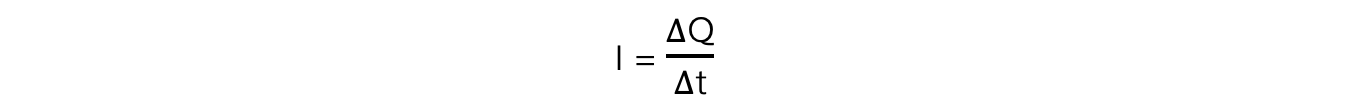
This means that the gradient of the charge-time graph is the current at that time
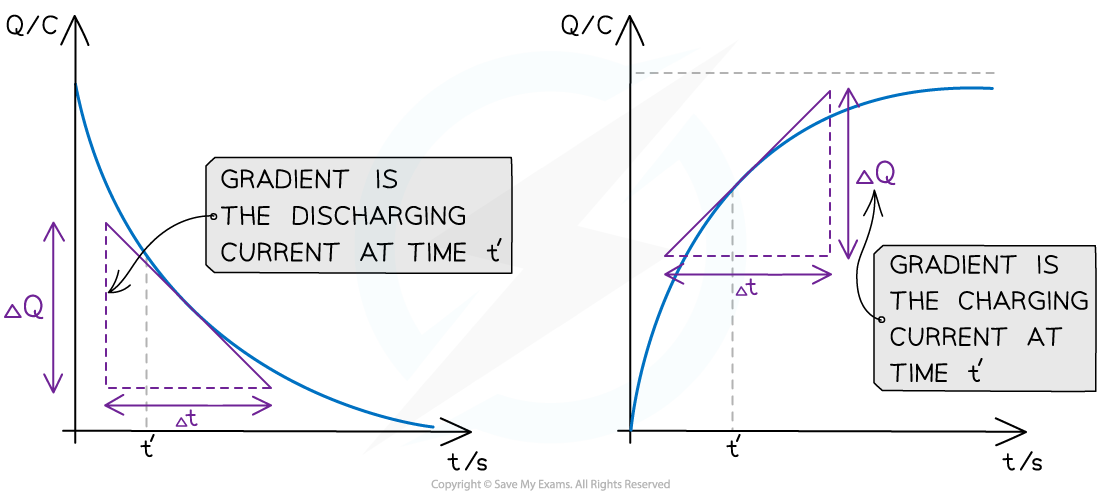
The gradient of a discharging and charging Q-t graph is the current
In the discharging graph, this is the discharging current at that time
In the charging graph, this is the charging current at that time
To calculate the gradient of a curve, draw a tangent at that point and calculate the gradient of that tangent
Worked Example
The graph below shows how the charge stored on a capacitor with capacitance C varies with time as it discharges through a resistor.
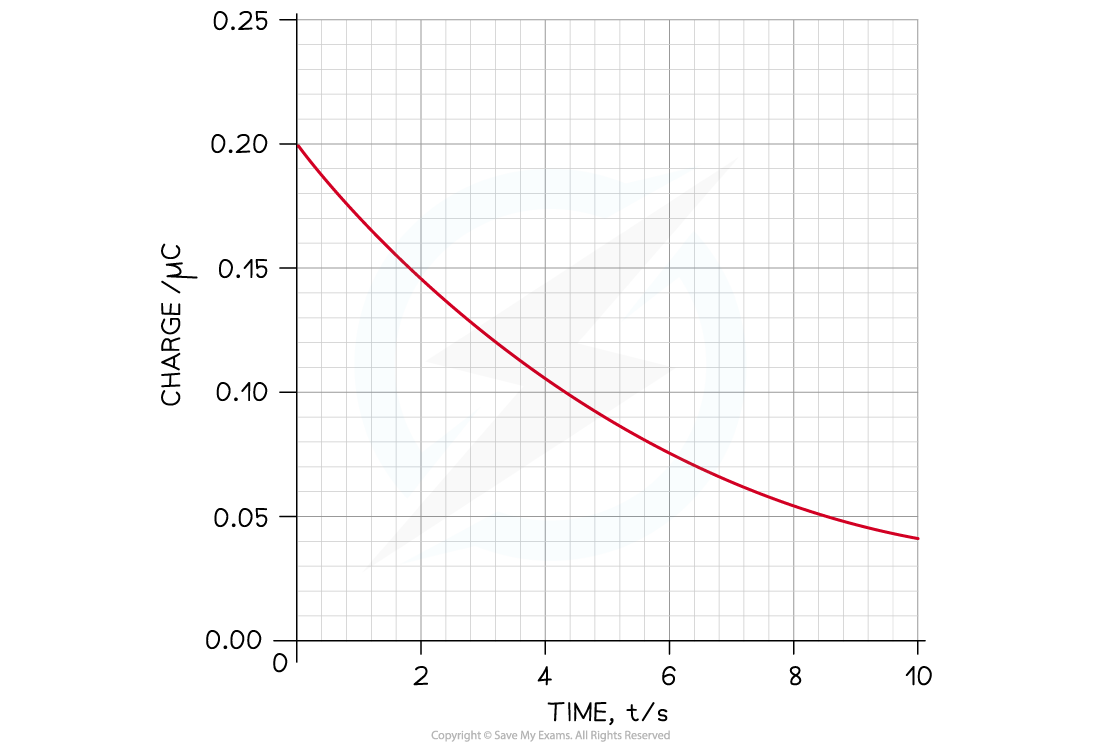
Calculate the current through the circuit after 4 s.
Answer:
Step 1: Draw a tangent at t = 4
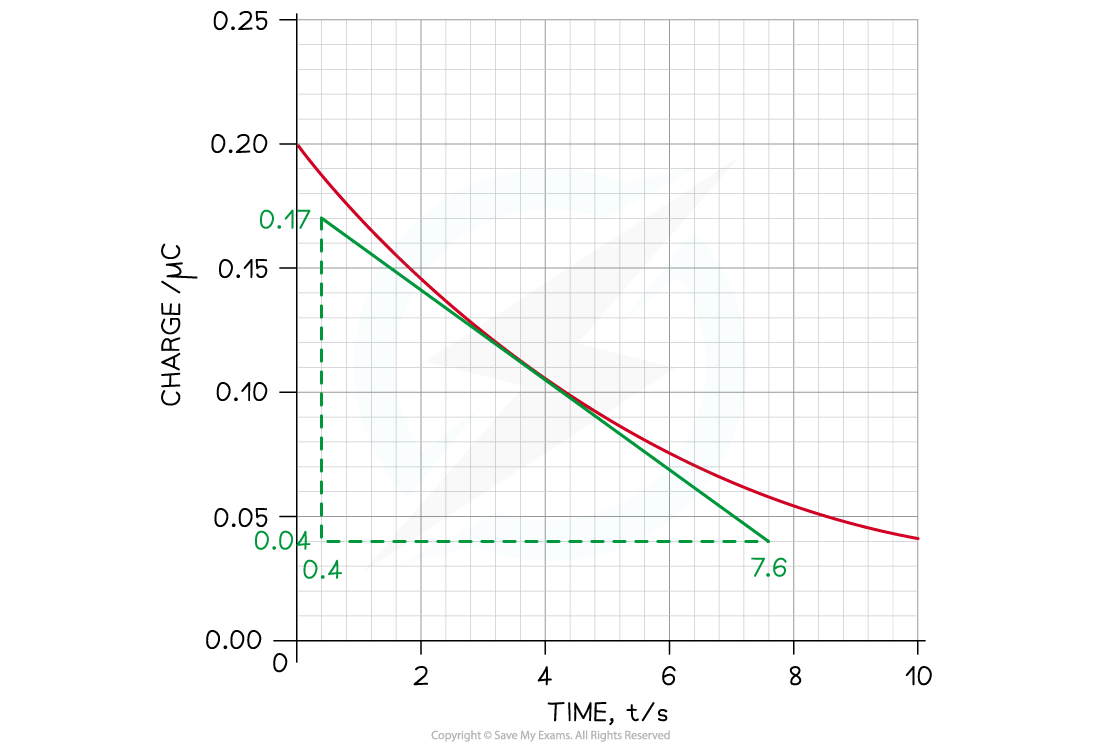
Step 2: Calculate the gradient of the tangent to find the current I
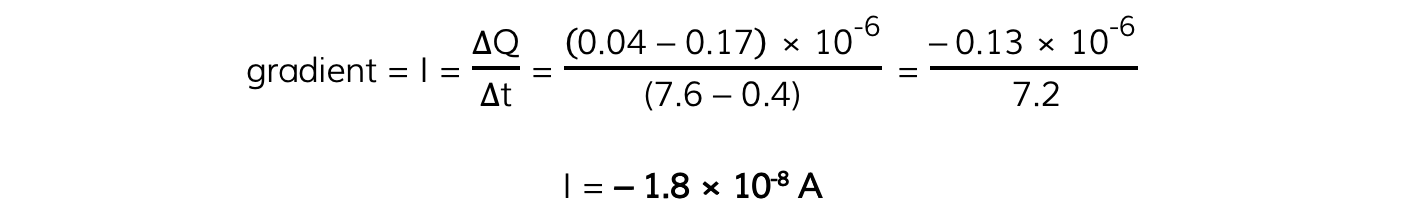

Unlock more, it's free!
Did this page help you?