Radial Electric Field (AQA A Level Physics)

Revision Note

Test yourself

Author

Katie M

Last updated

7 November 2024

Electric Field of a Point Charge

The strength of an electric field due to a point charge decreases with the square of the distance
- This is an inverse square law, similar to Coulomb's law
Using Coulomb's law and the electric field strength equation this can be written as

$E = \frac{F}{q} = \frac{Q}{4 π ε_{0} r^{2}}$

Where:
- Q = the point charge producing the radial electric field (C)
- r = distance from the centre of the charge (m)
- ε₀ = permittivity of free space (F m⁻¹)
Here, q represents the magnitude of a small positive test charge

This equation shows that in a radial electric field, the electric field strength E:
- is not constant
- follows an inverse square law with distance r

Graph of field strength against distance for a positive charge

4-2-6-electric-field-around-charged-sphere

Electric field strength is zero inside a charged sphere and decreases with distance outside the sphere according to an inverse square law

Combining Electric Fields

Both electric force and field strength are vector quantities
- If the charge is negative, the E field strength is negative and points towards the centre of the charge
- If the charge is positive, the E field strength is positive and points away from the centre of the charge

Therefore, to find the electric force or field strength at a point due to multiple charges, each field can be combined by vector addition

Vector addition of electric field along the same line

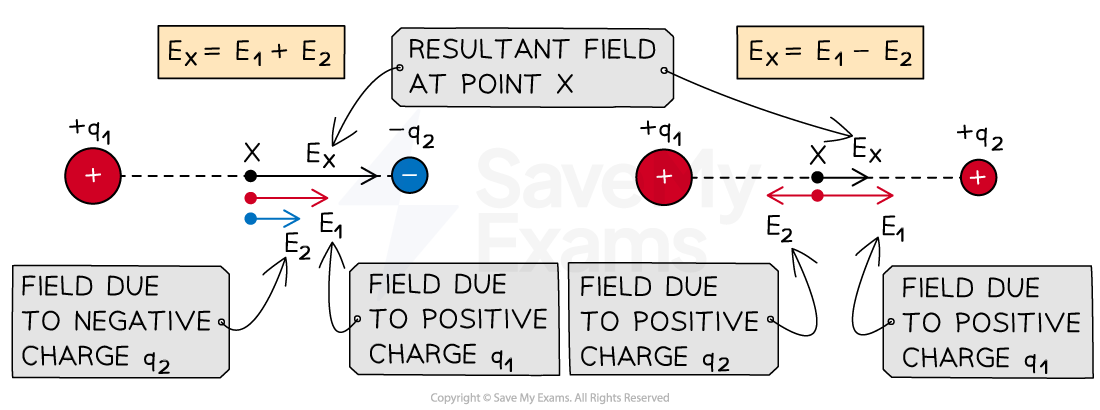
vector-addition-of-electric-field-strength

For charges along the same line, the resultant field is the vector addition of the field due to both charges at a particular point

For a point on the same line as two charges q₁ and q₂, with field strengths E₁ and E₂ respectively, the magnitude of the resultant field will be:
- The sum of the fields, E₁ + E₂, if they are both in the same direction
- The difference between the fields, E₁ − E₂, if they are in opposite directions

The direction of the resultant field depends on:
- The types of charge (positive or negative)
- The magnitude of the charges

For a point which makes a right-angled triangle with the charges, the resultant field can be determined using Pythagoras theorem

Vector addition of electric field components

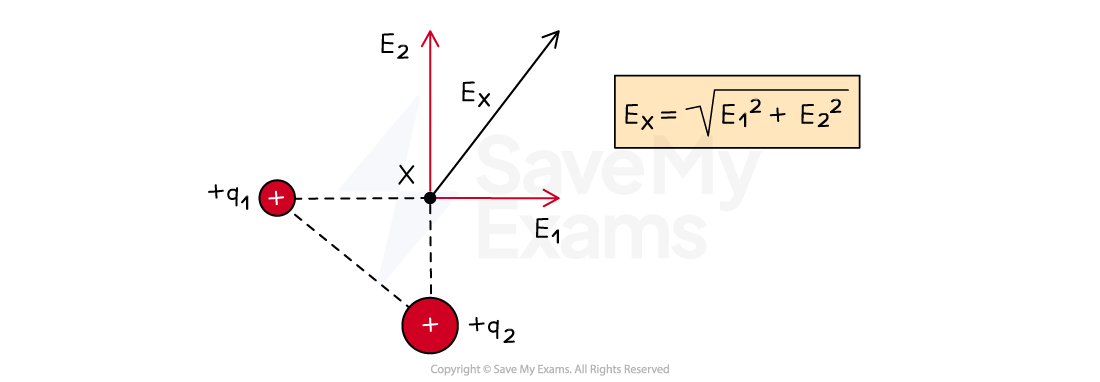
4-2-5-vector-addition-of-electric-field-strength-with-pythagoras

For charges which make a right-angle triangle with point X, the resultant field is the vector addition of the field due to both charges using Pythagoras theorem

Worked Example

A metal sphere of diameter 15 cm is negatively charged. The electric field strength at the surface of the sphere is 1.5 × 10⁵ V m⁻¹.

Determine the total surface charge of the sphere.

Answer:

Step 1: List the known quantities

Electric field strength, E = 1.5 × 10⁵ V m⁻¹
Radius of sphere, r = 15 / 2 = 7.5 cm = 7.5 × 10⁻² m
Permittivity of free space, ε₀ = 8.85 × 10⁻¹² F m⁻¹

Step 2: Write down the equation for electric field strength

$E = \frac{Q}{4 π ε_{0} r^{2}}$

Step 3: Rearrange for charge Q

Recall that, for an external observer, a charged sphere can be considered as a point charge
The field strength at the surface of the sphere is equal to the field strength 15 cm away from a point charge with the same total charge as the sphere

$Q = 4 π ε_{0} E r^{2}$

Step 4: Substitute in the values and calculate:

Q = (4π × 8.85 × 10⁻¹²) × (1.5 × 10⁵) × (7.5 × 10⁻²)² = 9.38 × 10⁻⁸ C

The particle has a charge of 9.4 × 10⁻⁸ C or 94 nC

Examiner Tips and Tricks

When combining electric fields from multiple charges, remember that the point (e.g. point X in the examples above) represents a positive test charge, so the direction of the electric force or field will correspond to the signs of the charges; the direction of the force or field points away from a positive charge and towards a negative charge.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves: