A LevelPhysicsAQARevision NotesFields & Their ConsequencesElectric FieldsUniform Electric Field

Uniform Electric Field (AQA A Level Physics)

Revision Note

Test yourself
Katie M

Author

Katie M

Last updated

Uniform Electric Field Strength

  • The magnitude of the electric field strength in a uniform field between two charged parallel plates is defined as:

E space equals space V over d

  • Where:

    • E = electric field strength (V m−1)

    • V = potential difference between the plates (V)

    • d = separation between the plates (m)

  • Note: both units for electric field strength, V m−1 and N C−1, are equivalent 

  • The equation shows:

    • The greater the voltage between the plates, the stronger the field

    • The greater the separation between the plates, the weaker the field

  • This equation cannot be used to find the electric field strength around a point charge

    • This is because the field around a point charge is radial

  • The electric field between two plates is directed:

    • From the positive plate (i.e. the one connected to the positive terminal)

    • To the negative plate (i.e. the one connected to the negative terminal)

Uniform Electric Field Between two Parallel Plates

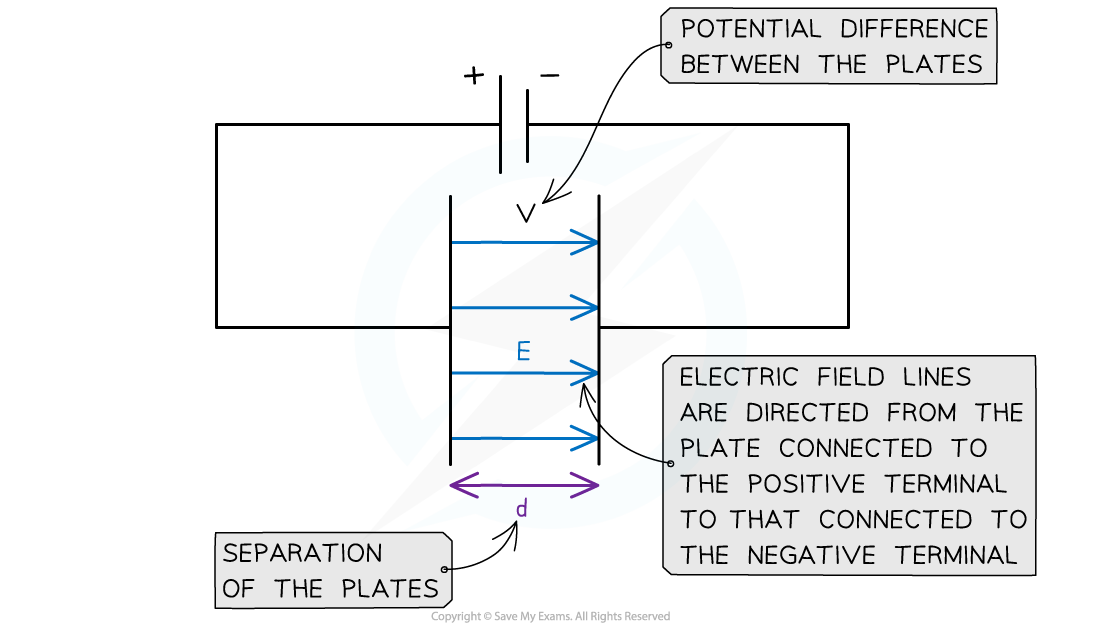
Electric field between two plates, downloadable AS & A Level Physics revision notes

The electric field strength between two charged parallel plates is the ratio of the potential difference and separation of the plates

Worked Example

Two parallel metal plates separated by 3.5 cm have a potential difference of 7.9 kV between them.

Calculate the electric force acting on a point charge of 2.6 × 10−15 C when placed between the plates.

Answer:

Step 1: List the known quantities

  • Potential difference between plates, V = 7.9 kV = 7900 V

  • Distance between plates, d = 3.5 cm = 0.035 m

  • Charge, Q = 2.6 × 10−15 C

Step 2: Equate the equations for electric field strength 

E field between parallel plates:  E space equals space V over d

E field on a point charge:  E space equals space F over Q

E space equals space F over Q space equals space V over d

Step 3: Rearrange the expression for electric force F

F space equals space fraction numerator Q V over denominator d end fraction

Step 4: Substitute values to calculate the force on the point charge

F space equals space fraction numerator open parentheses 2.6 cross times 10 to the power of negative 15 end exponent close parentheses cross times 7900 over denominator 0.035 end fraction space equals space 5.9 cross times 10 to the power of negative 10 end exponent N (2 s.f.)

Examiner Tips and Tricks

Remember the equation for electric field strength with V and d is only valid for parallel plates, and not for point charges 

However, when a point charge moves between two parallel plates, the two equations for electric field strength can be equated:

E space equals space F over Q space equals space V over d

Top tip: if one of the parallel plates is earthed, it has a voltage of 0 V

Derivation of Electric Field Strength Between Plates

  • When two points in an electric field have a different potential, there is a potential difference between them

    • To move a charge across that potential difference, work needs to be done

    • Two parallel plates with a potential difference V across them create a uniform electric field

  • The electric field strength between the plates is given by the equations:

E space equals space F over Q space equals space V over d

  • Rearranging the fractions by multiplying by Q and d on both sides, gives:

F d space equals space V Q

  • When a charge Q moves from one plate to the other, the work done on the charge by the field is

W space equals space F d

  • Where:

    • W = work done on charge (J)

    • F = electrostatic force (N)

    • d = distance between plates (m)

Parallel Plates Work Done, downloadable AS & A Level Physics revision notes

The work done on the charge depends on the electric force and the distance between the plates

  • Therefore, the work done in moving a charge Q through a potential difference V between parallel plates is also given by:

W space equals space Q V

Worked Example

Calculate the electrostatic force on an electron between two parallel plates 20 cm apart and have a potential difference of 400 V applied between them.

Answer:

Step 1: List the known quantities

  • Potential difference, V = 400 V

  • Distance between plates, d = 20 cm = 0.2 m

  • Charge of an electron, Q = 1.60 × 10−19 C

Step 2: Write an expression for the electrostatic force between two parallel plates

E space equals space fraction numerator space F over denominator Q end fraction space equals space V over d

F space equals space fraction numerator Q V over denominator d end fraction

Step 3: Substitute the values into the expression

F space equals space fraction numerator 400 cross times open parentheses 1.60 cross times 10 to the power of negative 19 end exponent close parentheses over denominator 0.2 end fraction space equals space 3.2 cross times 10 to the power of negative 16 end exponent N

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Electric Field StrengthNext:Motion of Charged Particles
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.