Geostationary Orbits

Synchronous Orbits

When an orbiting body has a time period equal to that of the body being orbited and in the same direction of rotation as that body

These usually refer to satellites (the orbiting body) around planets (the body being orbited)
The orbit of a synchronous satellite can be above any point on the planet's surface and in any plane
- When the plane of the orbit is directly above the equator, it is known as a geosynchronous orbit

Many communication satellites around Earth follow a geostationary orbit
- This is sometimes referred to as a geosynchronous orbit
This is a specific type of orbit in which the satellite:
- Remains directly above the equator
- Is in the plane of the equator
- Always orbits at the same point above the Earth’s surface
- Moves from west to east (same direction as the Earth spins)
- Has an orbital time period equal to Earth’s rotational period of 24 hours

Geostationary satellites are used for telecommunication transmissions (e.g. radio) and television broadcast
A base station on Earth sends the TV signal up to the satellite where it is amplified and broadcast back to the ground to the desired locations
The satellite receiver dishes on the surface must point towards the same point in the sky
- Since the geostationary orbits of the satellites are fixed, the receiver dishes can be fixed too

Some satellites are in low orbits, which means their altitude is closer to the Earth's surface
One example of this is a polar orbit, where the satellite orbits around the north and south pole of the Earth
Low orbits are useful for taking high-quality photographs of the Earth's surface. This could be used for:
- Weather
- Military applications

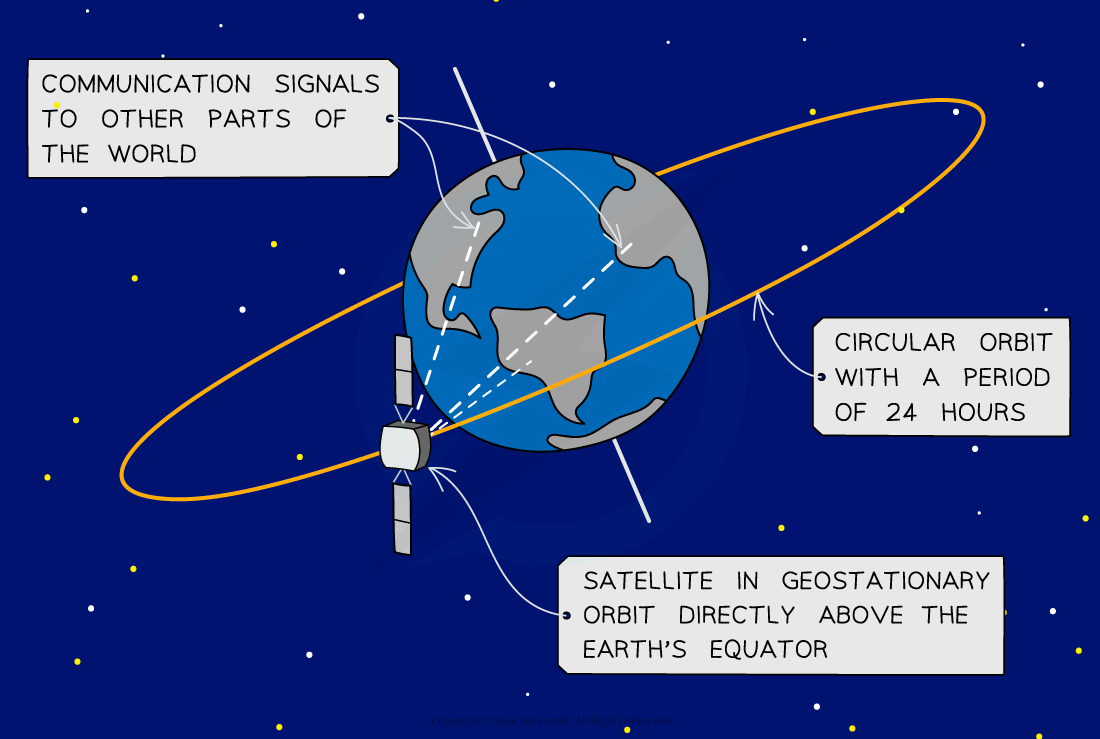
Geostationary orbit satellite, downloadable AS & A Level Physics revision notes

Geostationary satellite in orbit

The table gives data for two types of satellite, a low-Earth orbit (LEO) and a geostationary orbit

For the geostationary orbit, calculate

(i)

the orbital period X in minutes.

(ii)

the height Y above the Earth's surface that a geostationary satellite will orbit in km.

(i)

Step 1: Convert the time period from seconds to minutes

- The period of a geostationary orbit is X = 24 hrs
- The period of a geostationary orbit is X = 24 × 60 = 1440 minutes

(ii)

Step 1: List the known quantities

- Period of the LEO, T_L = 89 min
- Period of a geostationary orbit, T_G = 1440 min
- Height above Earth of the LEO, h_L = 250 km
- Radius of the Earth, R = 6.37 × 10⁶ m (from the data sheet)

Step 2: Recall the relationship between orbital period and radius

- Orbital period T is related to the radius r of the orbit by $T^{2} \propto r^{3}$

Step 3: Convert the proportional relationship into an equation

- $\frac{{T_{G}}^{2}}{{T_{L}}^{2}} = \frac{{r_{G}}^{3}}{{r_{L}}^{3}} \Rightarrow {r_{G}}^{3} = {r_{L}}^{3} {(\frac{T_{G}}{T_{L}})}^{2}$
- $r_{G} = \sqrt[3]{{r_{L}}^{3} {(\frac{T_{G}}{T_{L}})}^{2}} \Rightarrow r_{G} = r_{L} {(\frac{T_{G}}{T_{L}})}^{\frac{2}{3}}$

Step 4: Evaluate a final value for Y

- Orbital radius of LEO: $r_{L} = R + h_{L} = (6.37 \times 10^{6}) + (250 \times 10^{3}) = 6.62 \times 10^{6} m$
- Orbital radius of geostationary: $r_{G} = (6.62 \times 10^{6}) {(\frac{1440}{89})}^{\frac{2}{3}} = 4.235 \times 10^{7} m$
- Height above the Earth's surface: Y = $(4.235 \times 10^{7}) - (6.37 \times 10^{6}) = 3.6 \times 10^{7} m$
- Height above the Earth's surface: Y = 36 000 km

Make sure to memorise the key features of a geostationary orbit, since this is a common exam question. Remember:

You will also be expected to remember that the time period of the orbit is 24 hours for calculations on a geostationary satellite.